7.8: SSS Similarity
- Page ID
- 5303
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Triangles are similar if their corresponding sides are proportional.
SSS Similarity Theorem
By definition, two triangles are similar if all their corresponding angles are congruent and their corresponding sides are proportional. It is not necessary to check all angles and sides in order to tell if two triangles are similar. In fact, if you know only that all sides are proportional, that is enough information to know that the triangles are similar. This is called the SSS Similarity Theorem.
SSS Similarity Theorem: If all three pairs of corresponding sides of two triangles are proportional, then the two triangles are similar.
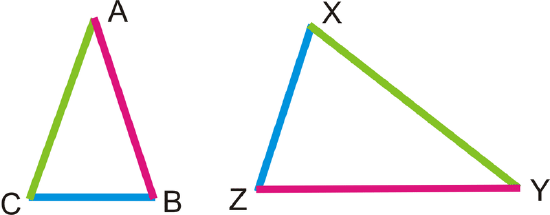
If \(\dfrac{AB}{YZ}=\dfrac{BC}{ZX}=\frac{AC}{XY}\), then \(\Delta ABC\sim \Delta YZX\).
What if you were given a pair of triangles and the side lengths for all three of their sides? How could you use this information to determine if the two triangles are similar?
For Examples 1 and 2, use the following diagram:
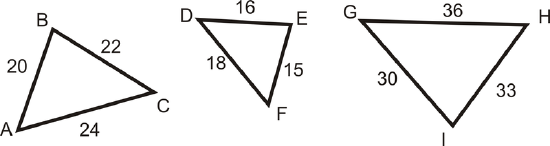
Example \(\PageIndex{1}\)
Is \(\Delta DEF\sim \Delta GHI\)?
Is \(\dfrac{15}{30}=\dfrac{16}{33}=\dfrac{18}{36}\)?
Solution
\(\dfrac{15}{30}=\dfrac{1}{2}\), \(\dfrac{16}{33}=\dfrac{16}{33}\), and \(\dfrac{18}{36}=\dfrac{1}{2}\). \(\dfrac{1}{2}\neq \dfrac{16}{33}\), \(\Delta DEF\) is not similar to \(\Delta GHI\).
Example \(\PageIndex{2}\)
Is \(\Delta ABC\sim \Delta GHI\)?
Is \(\dfrac{20}{30}=\dfrac{22}{33}=\dfrac{24}{36}\)?
Solution
\(\dfrac{20}{30}=dfrac{2}{3}\), \(\dfrac{22}{33}=\dfrac{2}{3}\), and \(\dfrac{24}{36}=\dfrac{2}{3}\). All three ratios reduce to \(\dfrac{2}{3}\), \(\Delta ABC\sim \Delta GHI\).
Example \(\PageIndex{3}\)
Determine if the following triangles are similar. If so, explain why and write the similarity statement.
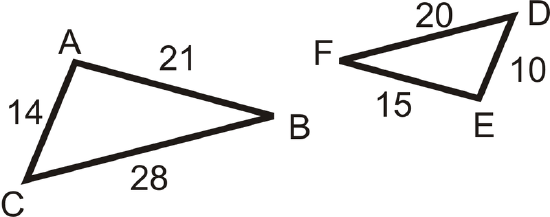
Solution
We will need to find the ratios for the corresponding sides of the triangles and see if they are all the same. Start with the longest sides and work down to the shortest sides.
\(\begin{aligned} \dfrac{BC}{FD}&=\dfrac{28}{20}=\dfrac{7}{5} \\ \dfrac{BA}{FE}&=\dfrac{21}{15}=\dfrac{7}{5} \\ \dfrac{AC}{ED}&=\dfrac{14}{10}=\dfrac{7}{5}\end{aligned}\)
Since all the ratios are the same, \(\Delta ABC\sim \Delta EFD\) by the SSS Similarity Theorem.
Example \(\PageIndex{4}\)
Find \(x and \(y, such that \(\Delta ABC\sim \Delta DEF\).
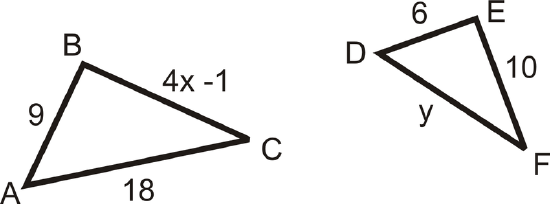
Solution
According to the similarity statement, the corresponding sides are: \(\dfrac{AB}{DE}=\dfrac{BC}{EF}=\dfrac{AC}{DF}\). Substituting in what we know, we have \(\dfrac{9}{6}=\dfrac{4x−1}{10}=\dfrac{18}{y}\).
\(\begin{aligned}
\frac{9}{6} &=\frac{4 x-1}{10} & \frac{9}{6} &=\frac{18}{y} \\
9(10) &=6(4 x-1) & & 9 y=18(6) \\
90 &=24 x-6 & & 9 y=108 \\
96 &=24 x & & y=12 \\
x &=4 &
\end{aligned}\)
Example \(\PageIndex{5}\)
Determine if the following triangles are similar. If so, explain why and write the similarity statement.
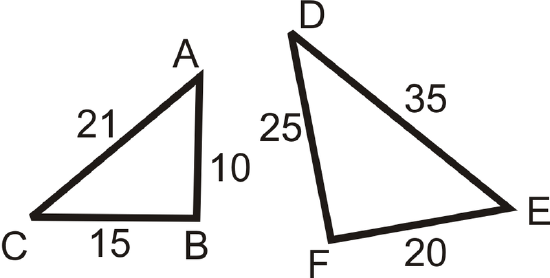
Solution
We will need to find the ratios for the corresponding sides of the triangles and see if they are all the same. Start with the longest sides and work down to the shortest sides.
\(\begin{aligned} \dfrac{AC}{ED}&=\dfrac{21}{35}=\dfrac{3}{5} \\ \dfrac{BC}{FD}&=\dfrac{15}{25}=\dfrac{3}{5} \\ \dfrac{AB}{EF}&=\dfrac{10}{20}=\dfrac{1}{2} \end{aligned}\)
Since the ratios are not all the same, the triangles are not similar.
Review
Fill in the blanks.
- If all three sides in one triangle are __________________ to the three sides in another, then the two triangles are similar.
- Two triangles are similar if the corresponding sides are _____________.
Use the following diagram for questions 3-5. The diagram is to scale.
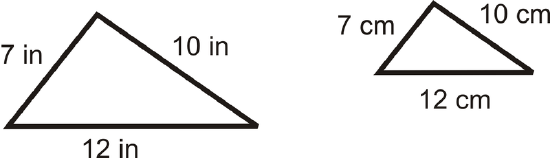
- Are the two triangles similar? Explain your answer.
- Are the two triangles congruent? Explain your answer.
- What is the scale factor for the two triangles?
Fill in the blanks in the statements below. Use the diagram to the left.
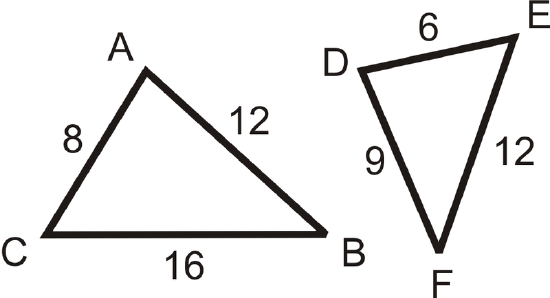
- \(\Delta ABC\sim \Delta _____\)
- \(\dfrac{AB}{?}=\dfrac{BC}{?}=\dfrac{AC}{?}\)
- If \(\Delta ABC\) had an altitude, \(AG=10\), what would be the length of altitude \(\overline{DH}\)?
- Find the perimeter of \(\Delta ABC\) and \(\Delta DEF\). Find the ratio of the perimeters.
Use the diagram to the right for questions 10-15.
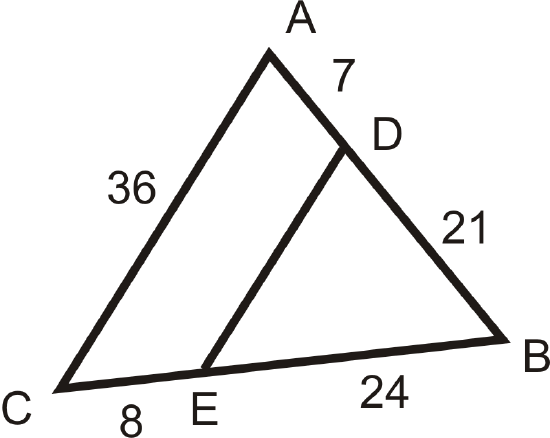Figure \(\PageIndex{8}\)- \(\Delta ABC\sim \Delta _____\)
- Why are the two triangles similar?
- Find \(ED\).
- \(\dfrac{BD}{?}=\dfrac{?}{BC}=\dfrac{DE}{?}\)
- Is \(\dfrac{AD}{DB}=\dfrac{CE}{EB}\) true?
- Is \(\dfrac{AD}{DB}=\dfrac{AC}{DE}\) true?
Find the value of the missing variable(s) that makes the two triangles similar.
-
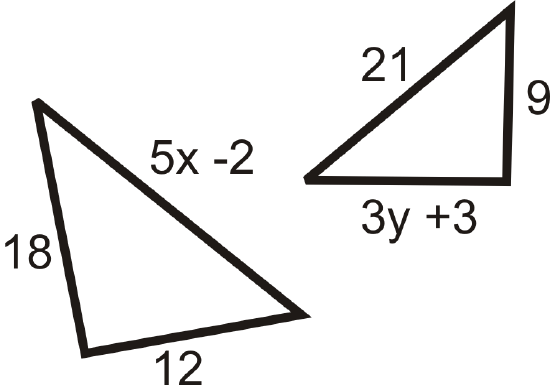
Figure \(\PageIndex{9}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 7.6.
Resources
Vocabulary
| Term | Definition |
|---|---|
| AAA Similarity Theorem | AAA Similarity Theorem states that if all three pairs of corresponding sides of two triangles are proportional, then the two triangles are similar. |
| Congruent | Congruent figures are identical in size, shape and measure. |
| Dilation | To reduce or enlarge a figure according to a scale factor is a dilation. |
| Ratio | A ratio is a comparison of two quantities that can be written in fraction form, with a colon or with the word “to”. |
| SSS | SSS means side, side, side and refers to the fact that all three sides of a triangle are known in a problem. |
| Rigid Transformation | A rigid transformation is a transformation that preserves distance and angles, it does not change the size or shape of the figure. |
Additional Resources
Interactive Element
Video: Congruent and Similar Triangles
Activities: SSS Similarity Discussion Questions
Study Aids: Polygon Similarity Study Guide
Practice: SSS Similarity
Real World: Crazy Quilt