7.7: AA Similarity
- Page ID
- 5302
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Two triangles are similar if two pairs of angles are congruent.
AA Similarity Postulate
By definition, two triangles are similar if all their corresponding angles are congruent and their corresponding sides are proportional. It is not necessary to check all angles and sides in order to tell if two triangles are similar. In fact, if you only know that two pairs of corresponding angles are congruent that is enough information to know that the triangles are similar. This is called the AA Similarity Postulate.
AA Similarity Postulate: If two angles in one triangle are congruent to two angles in another triangle, then the two triangles are similar.
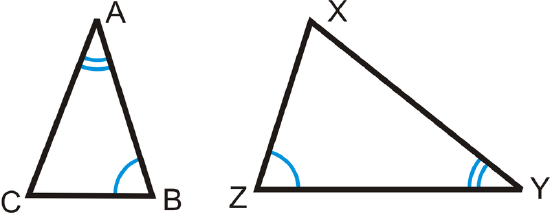
If \(\angle A\cong \angle Y\) and \(\angle B\cong \angle Z\), then \(\Delta ABC\sim \Delta YZX\).
What if you were given a pair of triangles and the angle measures for two of their angles? How could you use this information to determine if the two triangles are similar?
Example \(\PageIndex{1}\)
Are the triangles similar? If so, write a similarity statement.
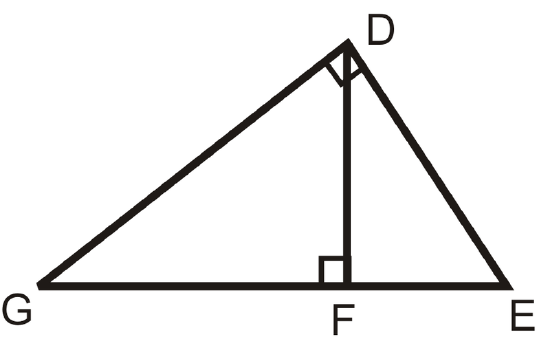
Solution
Yes, there are three similar triangles that each have a right angle. \(DGE\sim FGD\sim FDE\).
Example \(\PageIndex{2}\)
Are the triangles similar? If so, write a similarity statement.
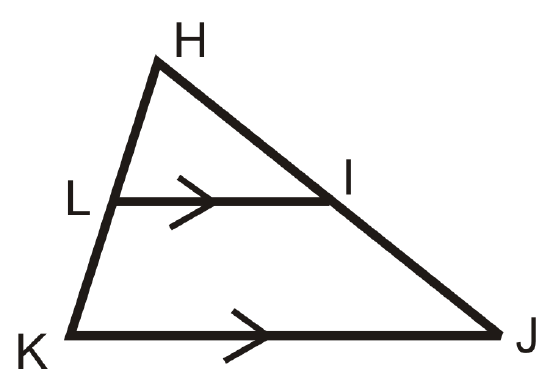
Solution
By the reflexive property, \(\angle H\cong \angle H\). Because the horizontal lines are parallel, \(\angle L\cong \angle K\) (corresponding angles). So yes, there is a pair of similar triangles. \(HLI\sim HKJ\).
Example \(\PageIndex{3}\)
Determine if the following two triangles are similar. If so, write the similarity statement.
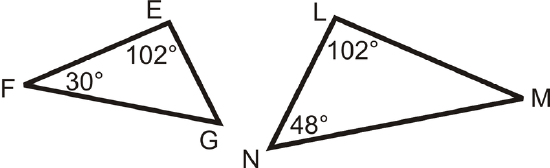
Solution
Compare the angles to see if we can use the AA Similarity Postulate. Using the Triangle Sum Theorem, \(m\angle G=48^{\circ}\) and \(m\angle M=30^{\circ}\). So, \(\angle F\cong \angle M\), \(\angle E\cong \angle L\) and \(\angle G\cong \angle N\) and the triangles are similar. \(\Delta FEG\sim \Delta MLN\).
Example \(\PageIndex{4}\)
Determine if the following two triangles are similar. If so, write the similarity statement.
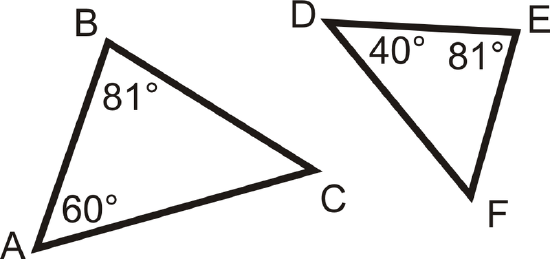
Solution
Compare the angles to see if we can use the AA Similarity Postulate. Using the Triangle Sum Theorem, \(m\angle C=39^{\circ}\) and \(m\angle F=59^{\circ}\). \(m\angle C\neq m\angle F\), So \(\Delta ABC\) and \(\Delta DEF\) are not similar.
Example \(\PageIndex{5}\)
\(\Delta LEG\sim \Delta MAR\) by AA. Find \(GE\) and \(MR\).
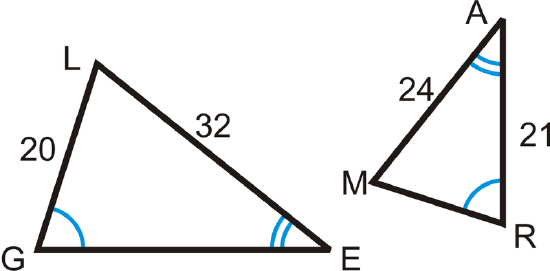
Solution
Set up a proportion to find the missing sides.
\(\begin{array}{rlrl}
\frac{24}{32} & =\frac{M R}{20} & \frac{24}{32} & =\frac{21}{G E} \\
480 & =32 M R & 24 G E & =672 \\
15 & =M R & G E&=28
\end{array}\)
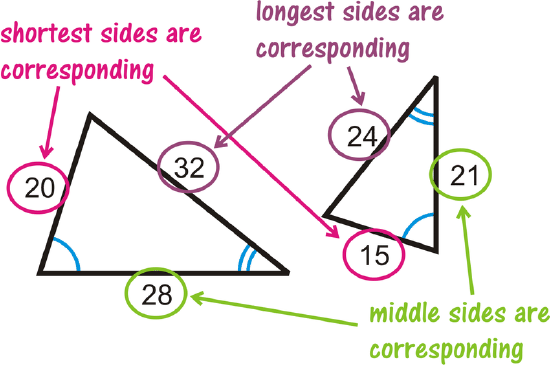
When two triangles are similar, the corresponding sides are proportional. But, what are the corresponding sides? Using the triangles from this example, we see how the sides line up in the diagram to the right.
Review
Use the diagram to complete each statement.
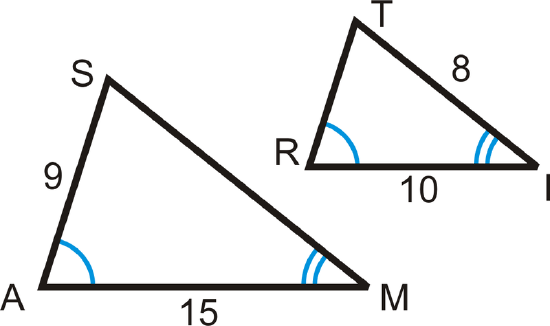
- \(\Delta SAM\sim \Delta ______\)
- \(\dfrac{SA}{?}=\dfrac{SM}{?}=\dfrac{?}{RI}\)
- \(SM = ______\)
- \(TR = ______\)
- \(\dfrac{9}{?}=\dfrac{?}{8}\)
Answer questions 6-9 about trapezoid \(ABCD\).
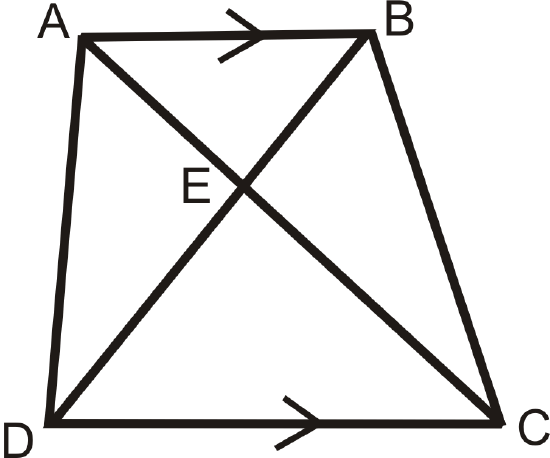
- Name two similar triangles. How do you know they are similar?
- Write a true proportion.
- Name two other triangles that might not be similar.
- If \(AB=10\), \(AE=7\), and \(DC=22\), find \(AC\). Be careful!
Use the triangles to the left for questions 10-14.
\(AB=20\), \(DE=15\), and \(BC=k\).
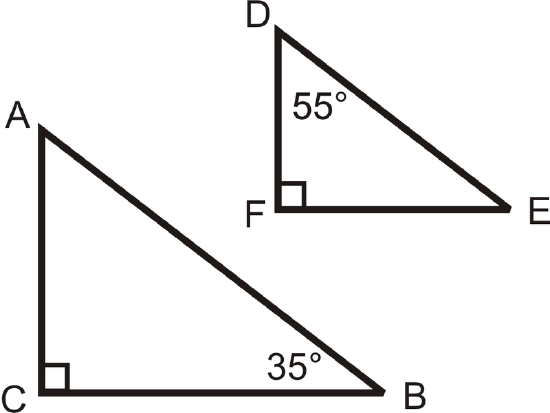
- Are the two triangles similar? How do you know?
- Write an expression for \(FE\) in terms of \(k\).
- If \(FE=12\), what is \(k\)?
- Fill in the blanks: If an acute angle of a _______ triangle is congruent to an acute angle in another ________ triangle, then the two triangles are _______.
- Writing How do congruent triangles and similar triangles differ? How are they the same?
Are the following triangles similar? If so, write a similarity statement.
-
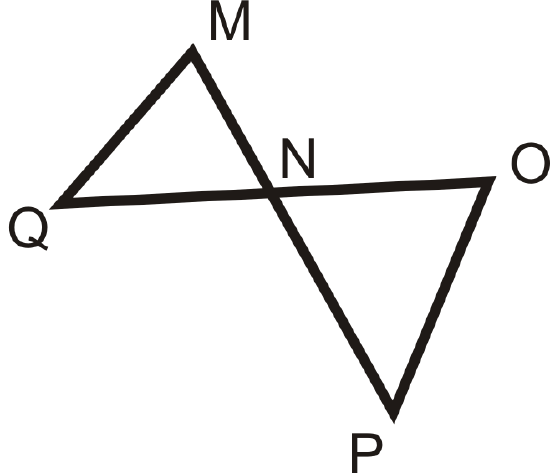
Figure \(\PageIndex{11}\) -
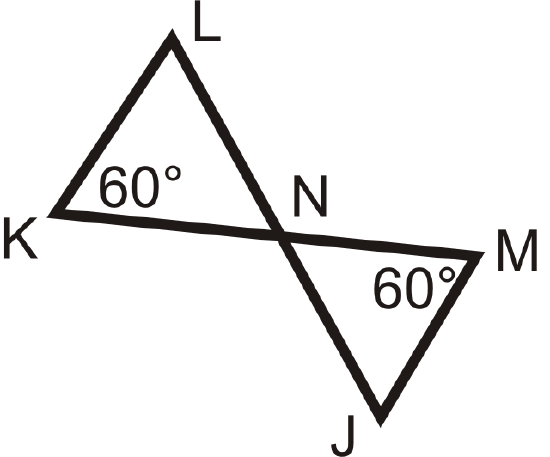
Figure \(\PageIndex{12}\) -
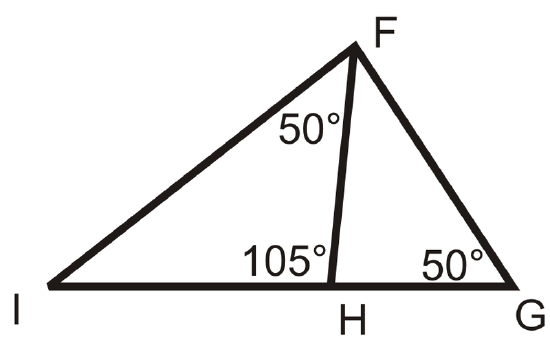
Figure \(\PageIndex{13}\) -
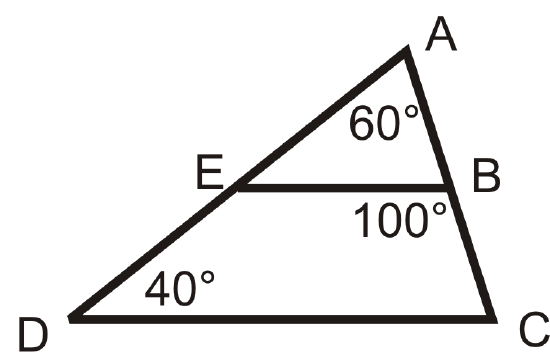
Figure \(\PageIndex{14}\) -
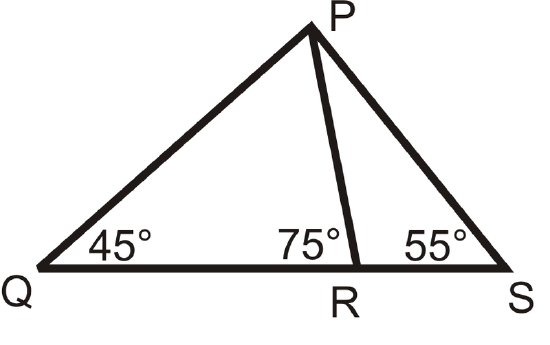
Figure \(\PageIndex{15}\) -
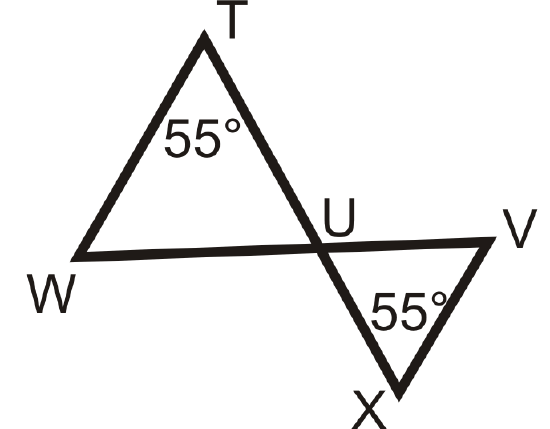
Figure \(\PageIndex{16}\) -
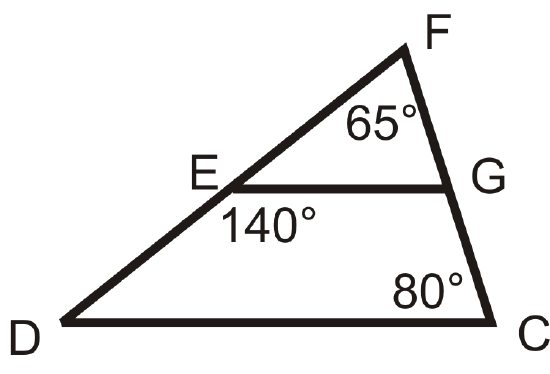
Figure \(\PageIndex{17}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 7.4.
Resources
Vocabulary
| Term | Definition |
|---|---|
| similar triangles | Two triangles where all their corresponding angles are congruent (exactly the same) and their corresponding sides are proportional (in the same ratio). |
| AA Similarity Postulate | If two angles in one triangle are congruent to two angles in another triangle, then the two triangles are similar. |
| Dilation | To reduce or enlarge a figure according to a scale factor is a dilation. |
| Triangle Sum Theorem | The Triangle Sum Theorem states that the three interior angles of any triangle add up to 180 degrees. |
| Rigid Transformation | A rigid transformation is a transformation that preserves distance and angles, it does not change the size or shape of the figure. |
Additional Resources
Interactive Element
Video: Congruent and Similar Triangles
Activities: AA Similarity Discussion Questions
Study Aids: Polygon Similarity Study Guide
Practice: AA Similarity
Real World: Crazy Quilt