8.13: Defining Reflection
- Page ID
- 6087
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Transformations that turn a figure into its mirror image by flipping it over a line.
Reflections
A transformation is an operation that moves, flips, or otherwise changes a figure to create a new figure. A rigid transformation (also known as an isometry or congruence transformation) is a transformation that does not change the size or shape of a figure.
The rigid transformations are translations, reflections, and rotations. The new figure created by a transformation is called the image. The original figure is called the preimage. If the preimage is A, then the image would be \(A′\), said “a prime.” If there is an image of \(A′\), that would be labeled \(A′′\), said “a double prime.”
A reflection is a transformation that turns a figure into its mirror image by flipping it over a line. The line of reflection is the line that a figure is reflected over. If a point is on the line of reflection then the image is the same as the preimage. Images are always congruent to preimages.

While you can reflect over any line, some common lines of reflection have rules that are worth memorizing:
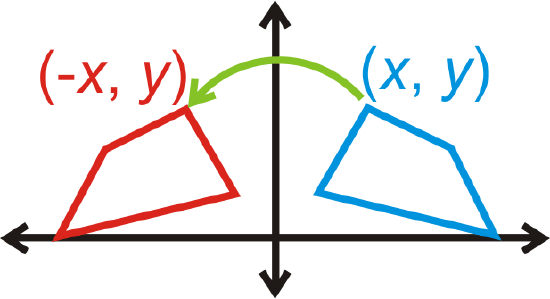
Reflection over the \(y\)-axis: \((x,y)\rightarrow (−x,y)\)
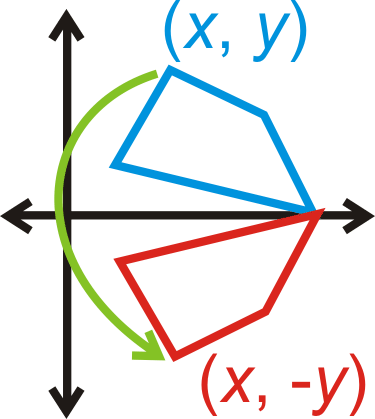
Reflection over the \(x\)-axis: \((x,y)\rightarrow (x,−y)\)
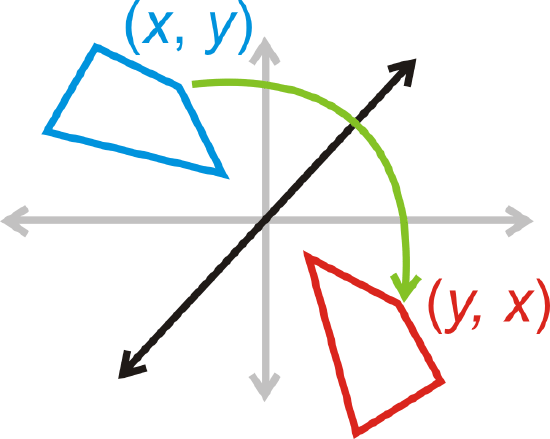
Reflection over \(y=x\): \((x,y)\rightarrow (y,x)\)
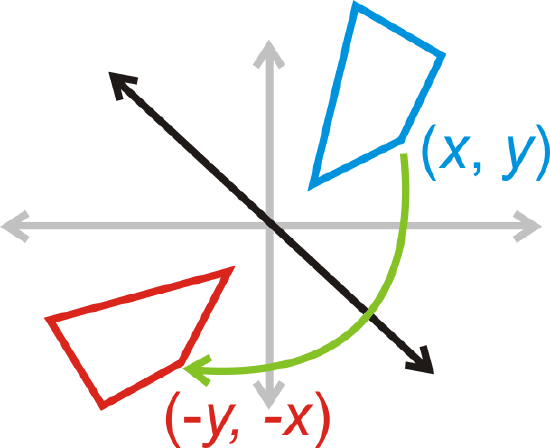
Reflection over \(y=−x\): \((x,y)\rightarrow (−y,−x)\)
What if you were given the coordinates of a quadrilateral and you were asked to reflect that quadrilateral over the \(y\)-axis? What would its new coordinates be?
Example \(\PageIndex{1}\)
Reflect \(\Delta ABC\) over the \(y\)-axis. Find the coordinates of the image.
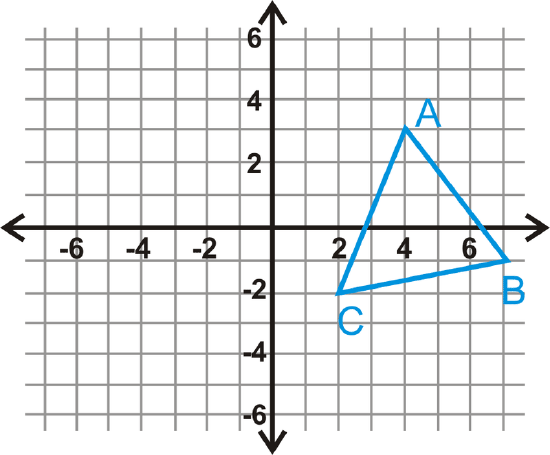
Solution
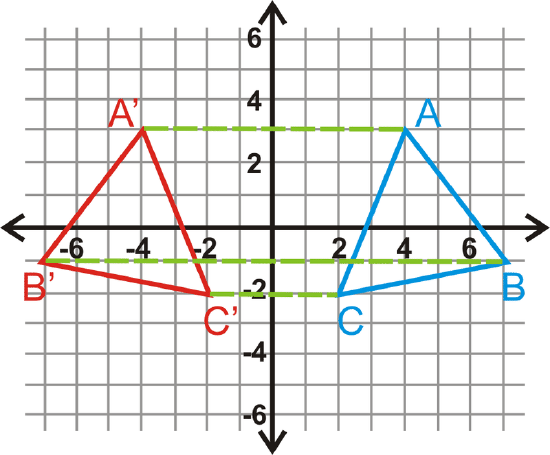
\(\Delta A′B′C′\) will be the same distance away from the \(y\)-axis as \(\Delta ABC\), but on the other side. Hence, their \(x\)-coordinates will be opposite.
\(\begin{aligned} &A(4,3)\rightarrow A′(−4,3) \\ &B(7,−1)\rightarrow B′(−7,−1) \\ &C(2,−2)\rightarrow C′(−2,−2)\end{aligned}\)
Example \(\PageIndex{2}\)
Reflect the letter ‘‘\(F\)′′ over the \(x\)-axis.
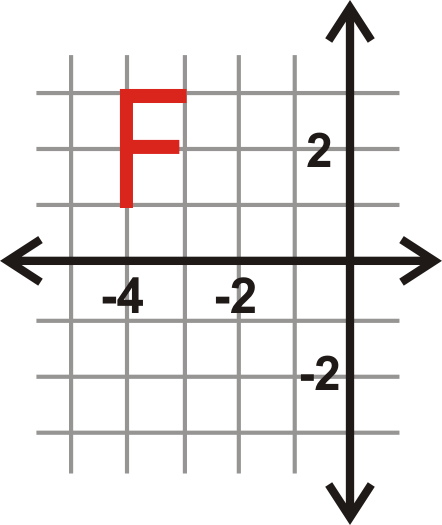
Solution
When reflecting the letter F over the \(x\)-axis, the \(y\)−coordinates will be the same distance away from the \(x\)-axis, but on the other side of the \(x\)-axis. Hence, their \(y\)-coordinates will be opposite.
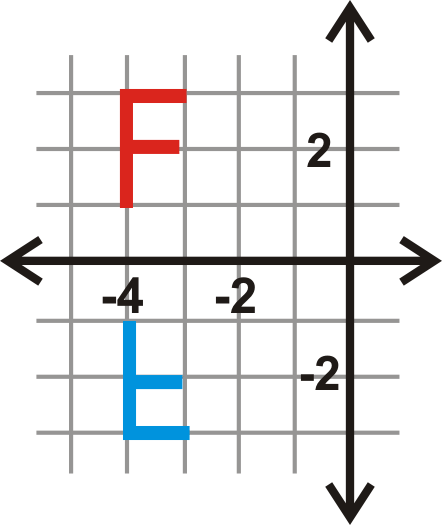
Example \(\PageIndex{3}\)
Reflect the triangle \(\Delta ABC\) with vertices \(A(4,5)\), \(B(7,1)\) and \(C(9,6)\) over the line \(x=5\). Find the coordinates of \(A′\), \(B′\), and \(C′\).
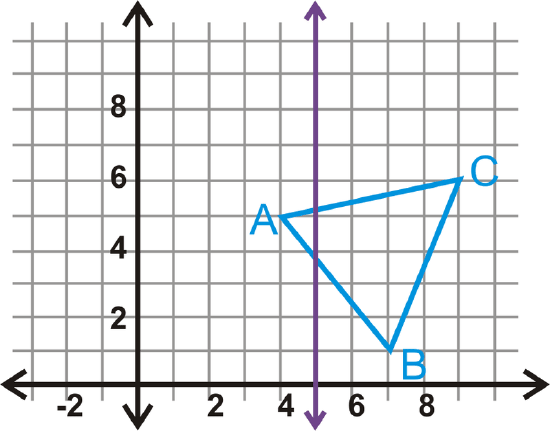
Solution
The image’s vertices are the same distance away from \(x=5\) as those of the preimage.
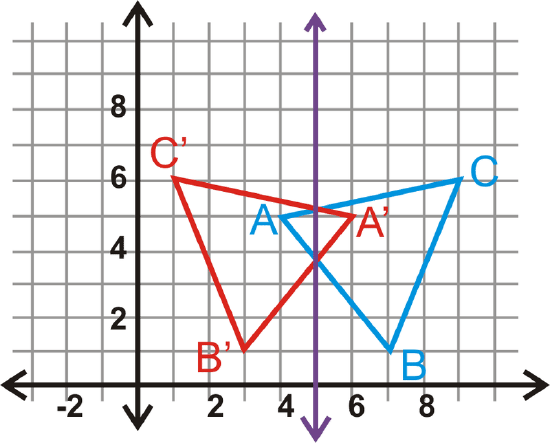
\(\begin{aligned} A(4,5)\rightarrow A′(6,5) \\ &B(7,1)\rightarrow B′(3,1) \\ &C(9,6)\rightarrow C′(1,6) \end{aligned}\)
Example \(\PageIndex{4}\)
Reflect the line segment \(\overline{PQ}\) with endpoints \(P(−1,5)\) and \(Q(7,8)\) over the line \(y=5\).
Solution
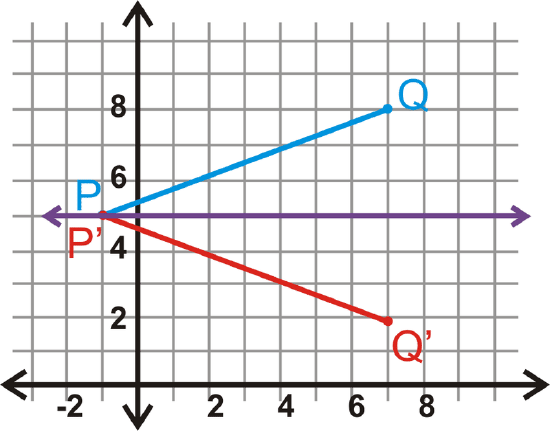
P is on the line of reflection, which means \(P′\) has the same coordinates. \(Q′\) is the same distance away from \(y=5, but on the other side.
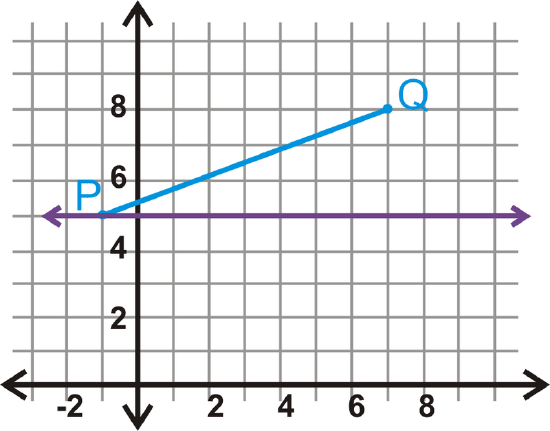
\(\begin{aligned}P(−1,5)&\rightarrow P′(−1,5) \\ Q(7,8)&\rightarrow Q′(7,2)\end{aligned}\)
Example \(\PageIndex{5}\)
A triangle \(\Delta LMN\) and its reflection, \(\Delta L′M′N′\) are below. What is the line of reflection?
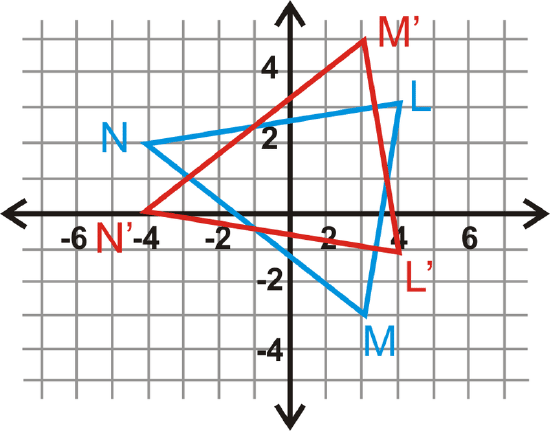
Solution
Looking at the graph, we see that the corresponding parts of the preimage and image intersect when \(y=1\). Therefore, this is the line of reflection.
If the image does not intersect the preimage, find the midpoint between the preimage point and its image. This point is on the line of reflection.
Example \(\PageIndex{6}\)
Reflect the trapezoid \(TRAP\) over the line \(y=−x\).
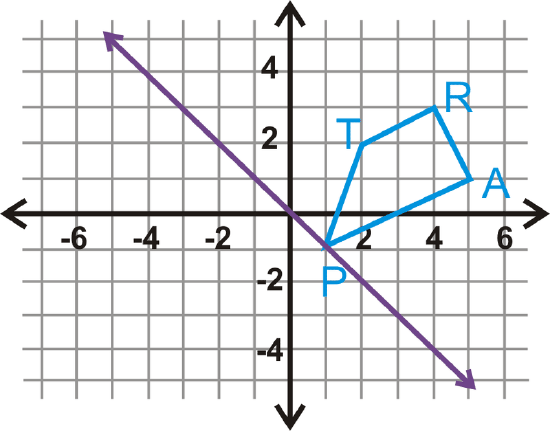
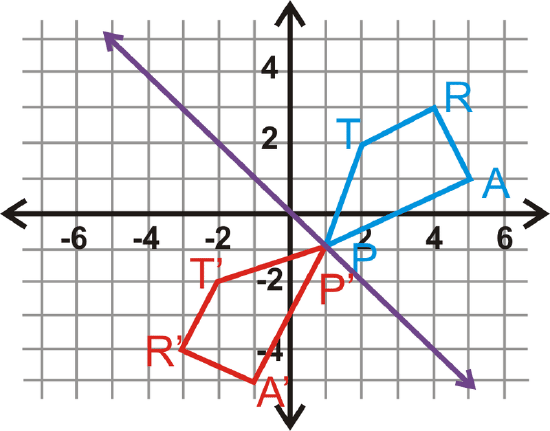
Solution
The purple line is \(y=−x\). You can reflect the trapezoid over this line.
\(\begin{aligned} T(2,2)\rightarrow T′(−2,−2) \\ R(4,3)\rightarrow R′(−3,−4) \\ A(5,1)&\rightarrow A′(−1,−5) \\ P(1,−1)&\rightarrow P′(1,−1) \end{aligned}\)
Review
- If \((5,3)\) is reflected over the \(y\)-axis, what is the image?
- If \((5,3)\) is reflected over the \(x\)-axis, what is the image?
- If \((5,3)\) is reflected over \(y=x\), what is the image?
- If \((5,3)\) is reflected over \(y=−x\), what is the image?
- Plot the four images. What shape do they make? Be specific.
- Which letter is a reflection over a vertical line of the letter ‘‘\(b\)′′?
- Which letter is a reflection over a horizontal line of the letter ‘‘\(b\)′′?
Reflect each shape over the given line.
- \(y\)-axis
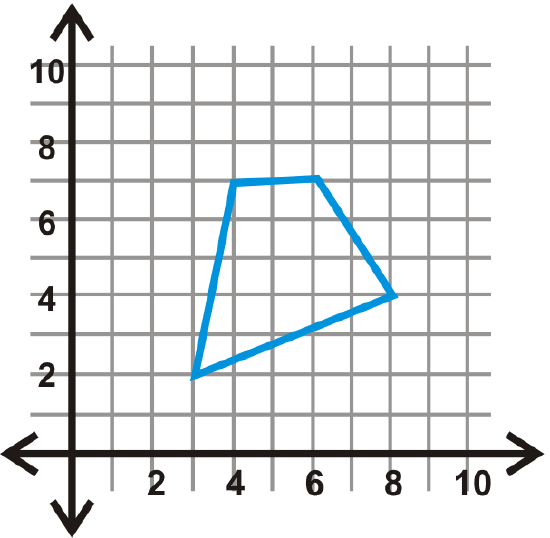
Figure \(\PageIndex{17}\) - \(x\)-axis
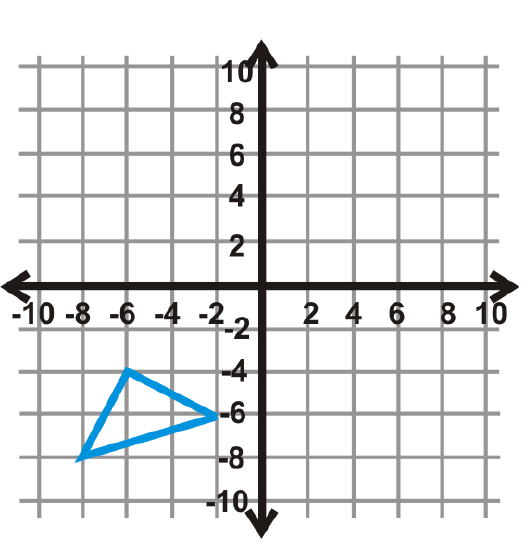
Figure \(\PageIndex{18}\) - \(y=3\)
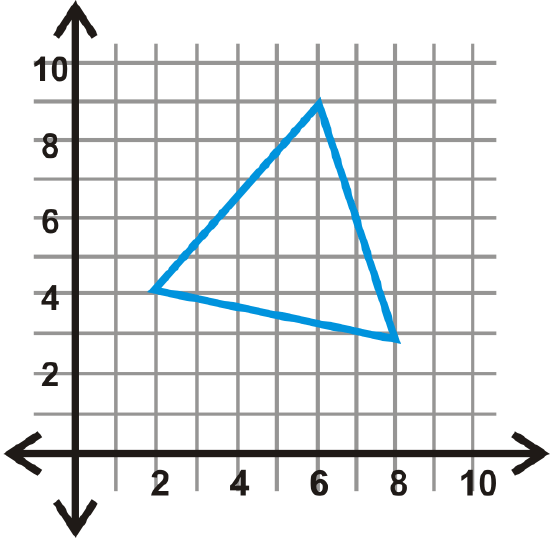
Figure \(\PageIndex{19}\) - \(x=−1\)
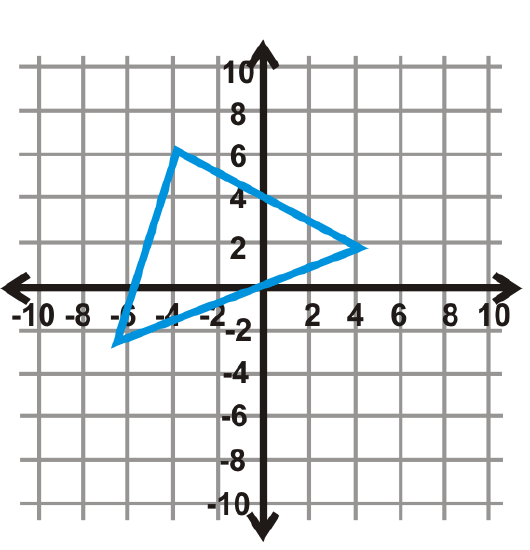
Figure \(\PageIndex{20}\) - \(x\)-axis
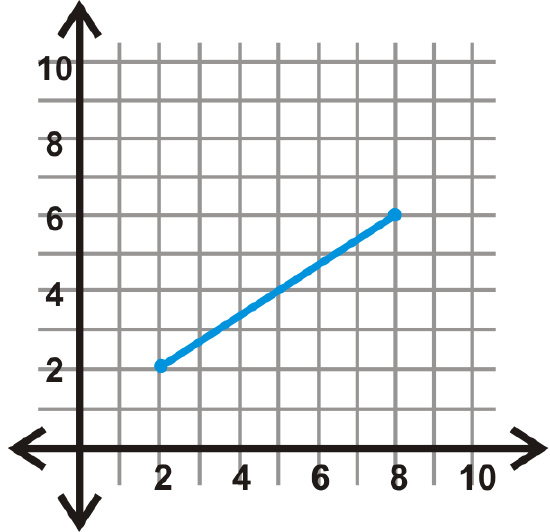
Figure \(\PageIndex{21}\) - \(y\)-axis
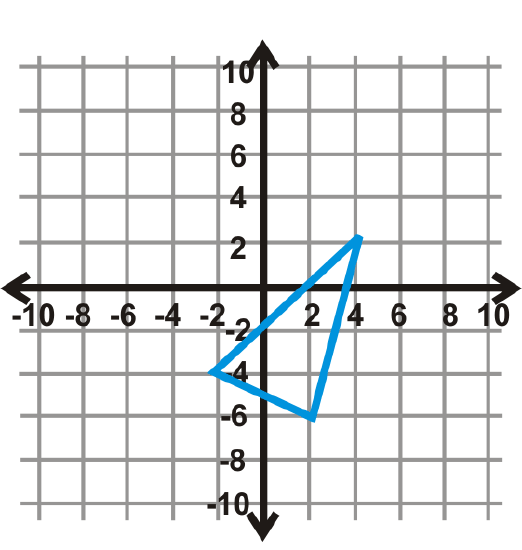
Figure \(\PageIndex{22}\) - \(y=x \)

Figure \(\PageIndex{23}\) - \(y=−x \)

Figure \(\PageIndex{24\) - \(x=2 \)

Figure \(\PageIndex{25}\) - \(y=−4 \)

Figure \(\PageIndex{26}\) - \(y=−x \)

Figure \(\PageIndex{27}\) - \(y=x \)

Figure \(\PageIndex{28}\)
Find the line of reflection the blue triangle (preimage) and the red triangle (image).
-
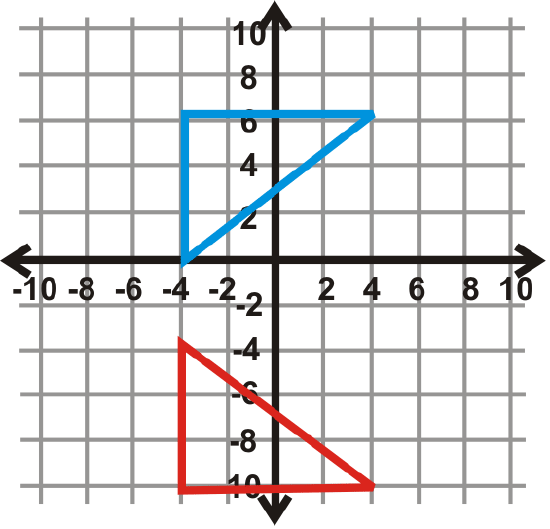
Figure \(\PageIndex{29}\) -
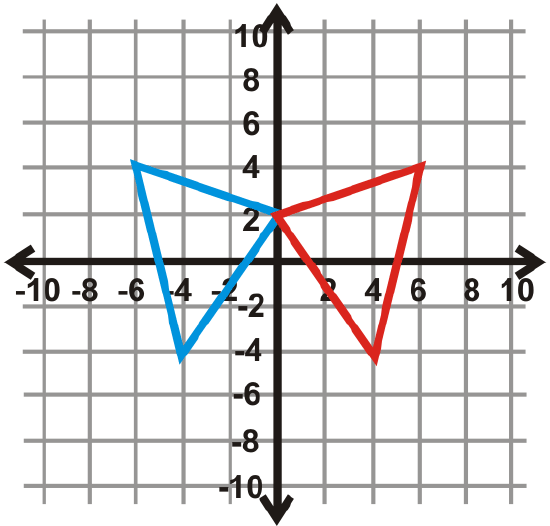
Figure \(\PageIndex{30}\) -
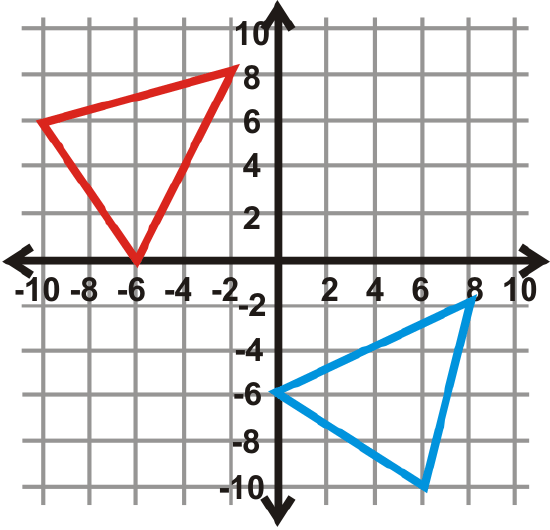
Figure \(\PageIndex{31}\)
Vocabulary
| Term | Definition |
|---|---|
| Coordinate Plane | The coordinate plane is a grid formed by a horizontal number line and a vertical number line that cross at the \((0, 0)\) point, called the origin. The coordinate plane is also called a Cartesian Plane. |
| Geometric Patterns | Geometric patterns are visual patterns of geometric figures that follow a rule. |
| Image | The image is the final appearance of a figure after a transformation operation. |
| perpendicular bisector | A perpendicular bisector of a line segment passes through the midpoint of the line segment and intersects the line segment at \(90^{\circ}\). |
| Perpendicular lines | Perpendicular lines are lines that intersect at a \(90^{\circ}\) angle. |
| Preimage | The pre-image is the original appearance of a figure in a transformation operation. |
| Reflection | A reflection is a transformation that flips a figure on the coordinate plane across a given line without changing the shape or size of the figure. |
| Transformation | A transformation moves a figure in some way on the coordinate plane. |
| Rigid Transformation | A rigid transformation is a transformation that preserves distance and angles, it does not change the size or shape of the figure. |
Review (Answers)
To see the Review answers, open this PDF file and look for section 12.5.
Additional Resources
Interactive Element
Video: Transformation: Reflection Principles - Basic
Activities: Reflections Discussion Questions
Study Aids: Types of Transformations Study Guide
Practice: Defining Reflection
Real World: Reflecting Reality

