8.14: Rules for Reflections

Identify and state rules describing reflections using notation

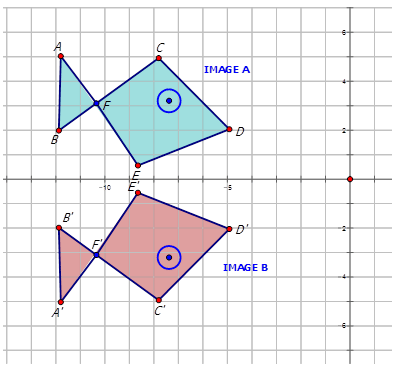
The figure below shows a pattern of two fish. Write the mapping rule for the reflection of Image \(A\) to Image \(B\).

Figure \(\PageIndex{1}\)

In geometry, a transformation is an operation that moves, flips, or changes a shape to create a new shape. A reflection is an example of a transformation that takes a shape (called the preimage) and flips it across a line (called the line of reflection) to create a new shape (called the image). By examining the coordinates of the reflected image, you can determine the line of reflection. The most common lines of reflection are the \(x\)-axis, the \(y\)-axis, or the lines \(y=x\) or\(y=−x\).

Figure \(\PageIndex{2}\)

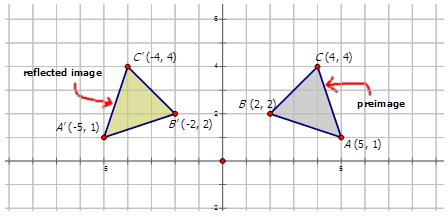
The preimage above has been reflected across the \(y\)-axis. This means, all of the x-coordinates have been multiplied by -1. You can describe the reflection in words, or with the following notation:

\(r_{y-axis} (x,y)\rightarrow (−x,y)\)

Notice that the notation tells you exactly how each \((x,y)\) point changes as a result of the transformation.

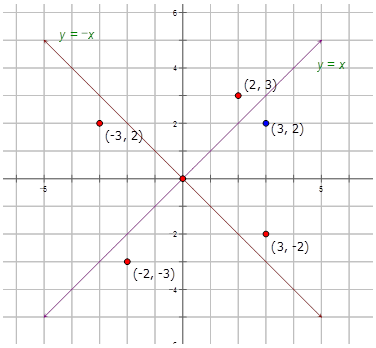
Let's find the image of the point \((3, 2)\) that has undergone a reflection across the following lines:

1. The \(x\)-axis,

Reflection across the \(x\)-axis: \(r_{x-axis} (3,2)\rightarrow (3,−2)\)

2. The \(y\)-axis

Reflection across the \(y\)-axis: \(r_{y-axis} (3,2)\rightarrow (3,−2)\)

3. The line \(y=x\)

Reflection across the line \(y=x\): \(r_{y=x} (3,2)\rightarrow (2,3)\)

4. The line\(y=−x\).

Reflection across the line\(y=−x\): \(r_{y=−x} (3,2)\rightarrow (−2,−3)\)

Figure \(\PageIndex{4}\)

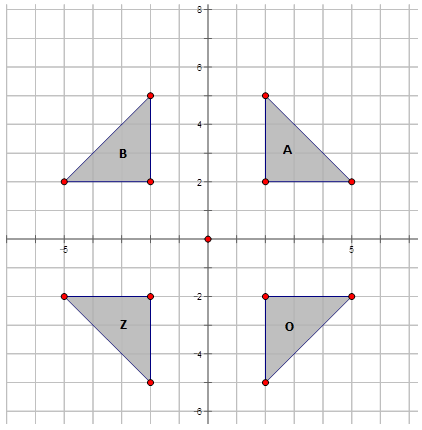
Now, let's reflect Image \(A\) in the diagram below across the following lines and write the notation for each reflection:

Figure \(\PageIndex{5}\)

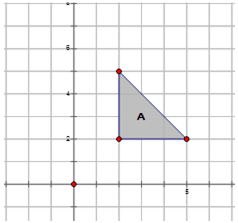
1. Across the \(y\)-axis and label it \(B\).

Reflection across the \(y\)-axis: \(r_{y-axis} A\rightarrow B=r_{y-axis} (x,y)\rightarrow (−x,y)\)

2. Across the \(x\)-axis and label it \(O\).

Reflection across the \(x\)-axis: \(r_{x-axis} A\rightarrow O=r_{x-axis} (x,y)\rightarrow (x,−y)\)

3. Across the line\(y=−x\) and label it \(Z\).

Reflection across the\(y=−x\): \(r_{y=−x} A\rightarrow Z=r_{y=−x} (x,y)\rightarrow (−y,−x) \)

Figure \(\PageIndex{6}\)

Finally, let's write the notation that represents the reflection of the preimage to the image in the diagram below:

Figure \(\PageIndex{7}\)

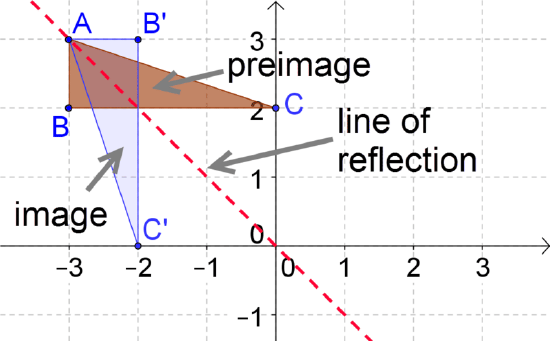
This is a reflection across the line\(y=−x\). The notation is \(r_{y=−x} (x,y)\rightarrow (−y,−x)\).

Example \(\PageIndex{1}\)

Earlier, you were given a problem about the figure below that shows a pattern of two fish. Write the mapping rule for the reflection of Image A\) to Image B\).

Figure \(\PageIndex{8}\)

Solution

To answer this question, look at the coordinate points for Image A and Image B.

Image A	\(A(−11.8,5)\)	\(B(−11.8,2)\)	\(C(−7.8,5)\)	\(D(−4.9,2)\)	\(E(−8.7,0.5)\)	\(F(−10.4,3.1)\)
Image B	\(A′(−11.8,−5)\)	\(B′(−11.8,−2)\)	\(C′(−7.8,−5)\)	\(D′(−4.9,−2)\)	\(E′(−8.7,−0.5)\)	\(F′(−10.4,−3.1)\)

Notice that all of the \(y-coordinates have changed sign. Therefore Image A has reflected across the \(x\)-axis. To write a rule for this reflection you would write: \(r_{x-axis} (x,y)\rightarrow (x,−y)\).

Example \(\PageIndex{2}\)

Thomas describes a reflection as point \(J moving from \(J(−2,6)\) to \(J′(−2,−6)\). Write the notation to describe this reflection for Thomas.

\(J:(−2,6)\qquad J′:(−2,−6)\)

Solution

Since the y-coordinate is multiplied by -1 and the \(x-coordinate remains the same, this is a reflection in the \(x\)-axis. The notation is: \(r_{x-axis} J\rightarrow J′=r_{x-axis} (−2,6)\rightarrow (−2,6)\)

Example \(\PageIndex{3}\)

Write the notation that represents the reflection of the yellow diamond to the reflected green diamond in the diagram below.

Figure \(\PageIndex{9}\)

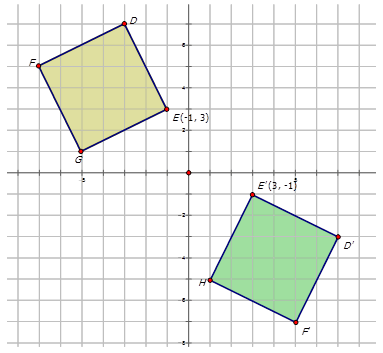
Solution

In order to write the notation to describe the reflection, choose one point on the preimage (the yellow diamond) and then the reflected point on the green diamond to see how the point has moved. Notice that point \(E\) is shown in the diagram:

\(E(−1,3)\rightarrow E′(3,−1)\)

Since both \(x\)- and \(y\)-coordinates are reversed numbers, the reflection is in the line \(y=x\). The notation for this reflection would be: \(r_{y=x} (x,y)\rightarrow (y,x)\).

Example \(\PageIndex{4}\)

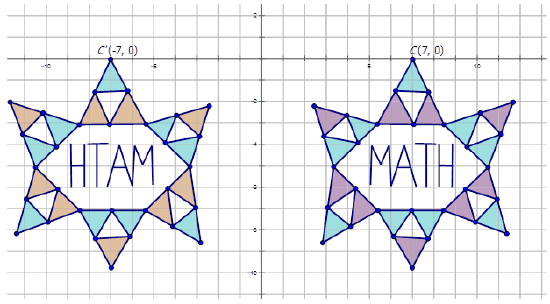
Karen was playing around with a drawing program on her computer. She created the following diagrams and then wanted to determine the transformations. Write the notation rule that represents the transformation of the purple and blue diagram to the orange and blue diagram.

Figure \(\PageIndex{10}\)

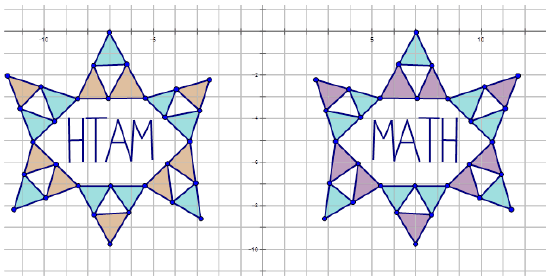
Solution

In order to write the notation to describe the transformation, choose one point on the preimage (purple and blue diagram) and then the transformed point on the orange and blue diagram to see how the point has moved. Notice that point A is shown in the diagram:

\(C(7,0)\rightarrow C′(−7,0)\)

Since both x-coordinates only are multiplied by -1, the transformation is a reflection is in \(y\)-axis. The notation for this reflection would be: \(r_{y-axis} (x,y)\rightarrow (−x,y)\).

Figure \(\PageIndex{11}\)

Review

Write the notation to describe the movement of the points in each of the reflections below.

1. \(S(1,5)\rightarrow S′(−1,5)\)
2. \(W(−5,−1)\rightarrow W′(5,−1)\)
3. \(Q(2,−5)\rightarrow Q′(2,5)\)
4. \(M(4,3)\rightarrow M′(−3,−4)\)
5. \(B(−4,−2)\rightarrow B′(−2,−4)\)
6. \(A(3,5)\rightarrow A′(−3,5)\)
7. \(C(1,2)\rightarrow C′(2,1)\)
8. \(D(2,−5)\rightarrow D′(5,−2)\)
9. \(E(3,1)\rightarrow E′(−3,1)\)
10. \(F(−4,2)\rightarrow F′(−4,−2)\)
11. \(G(1,3)\rightarrow G′(1,−3)\)

Write the notation that represents the reflection of the preimage image for each diagram below.

12. 

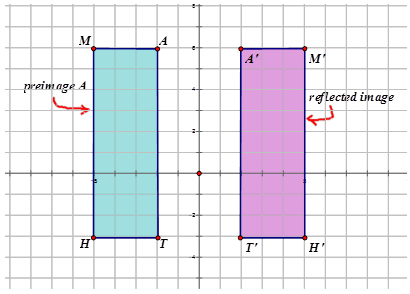
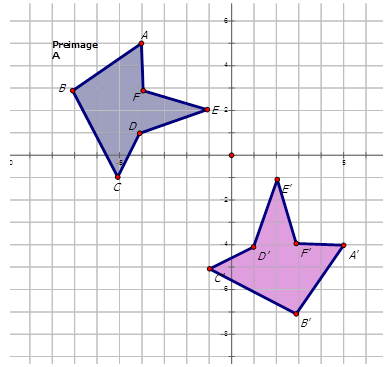
    Figure \(\PageIndex{12}\)

13. 

    Figure \(\PageIndex{13}\)

14. 

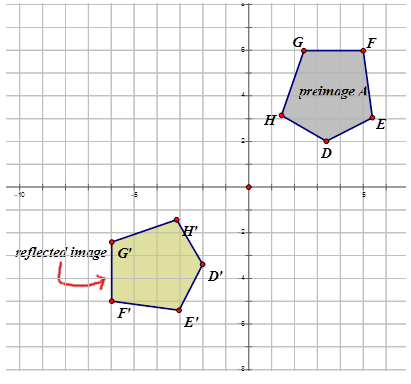
    Figure \(\PageIndex{14}\)

15. 

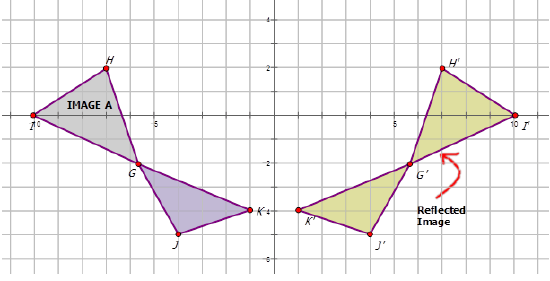
    Figure \(\PageIndex{15}\)

Review (Answers)

To see the Review answers, open this PDF file and look for section 10.6.

Additional Resources

Interactive Element

Practice: Rules for Reflections