8.15: Geometry Software for Reflections
- Page ID
- 6125
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Graph images given preimage and line of reflection. Perform reflections using Geogebra.
Graphs of Reflections
Triangle A has coordinates \(E(−5,−5)\), \(F(2,−6)\) and \(G(−2,0)\). Draw the triangle on the Cartesian plane. Reflect the image across the \(y\)-axis. State the coordinates of the resulting image.
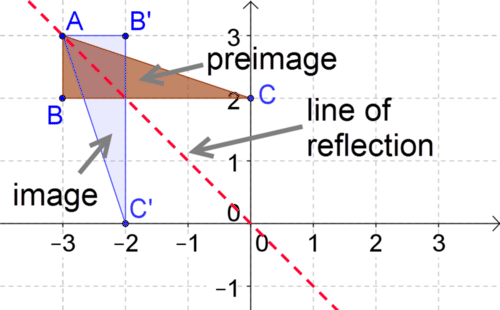
In geometry, a transformation is an operation that moves, flips, or changes a shape to create a new shape. A reflection is an example of a transformation that takes a shape (called the preimage) and flips it across a line (called the line of reflection) to create a new shape (called the image).
To graph a reflection, you can visualize what would happen if you flipped the shape across the line.
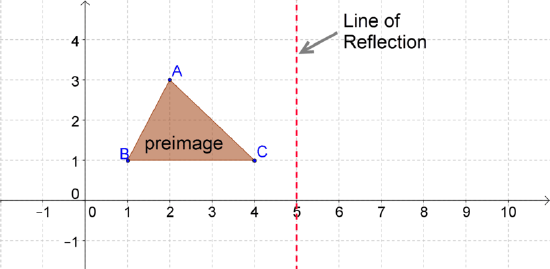
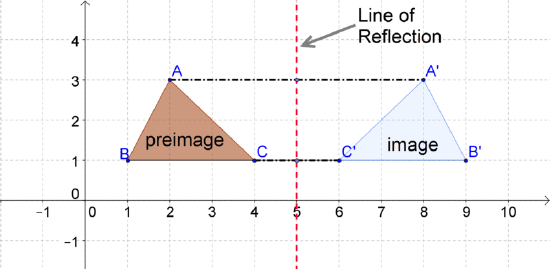
Each point on the preimage will be the same distance from the line of reflection as it's corresponding point in the image. For example, for the pair of triangles below, both \(A\) and \(A′\) are 3 units away from the line of reflection.
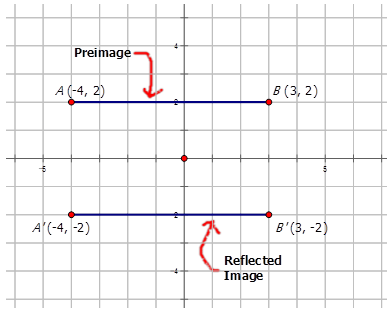
For common reflections, you can also remember what happens to their coordinates:
- reflections across the \(x\)-axis: \(y\) values are multiplied by -1.
- reflections across the \(y\)-axis: \(x\) values are multiplied by -1.
- reflections across the line \(y=x\): \(x\) and \(y\) values switch places.
- reflections across the line \(y=-x\). \(x\) and \(y\) values switch places and are multiplied by -1.
Knowing the rules above will allow you to recognize reflections even when a graph is not available.
Let's draw the reflections described in the following problems. Include the preimage if not given.
- Line \(\overline{AB}\) drawn from \((-4, 2)\) to \((3, 2)\) has been reflected across the \(x\)-axis.
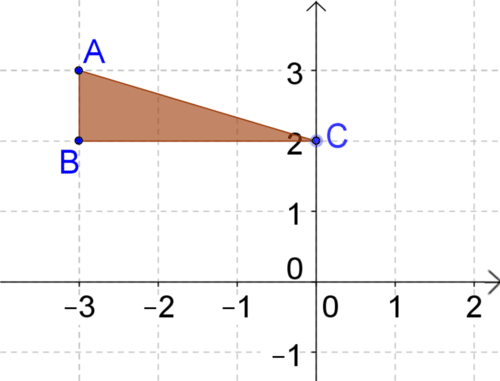
- Triangle \(ABC\) is reflected across the line \(y=-x\) to form the image \(A′B′C′\). Draw and label the reflected image.
Now, let's find find the coordinates of the following reflected image and draw the image:
The diamond \(ABCD\) is reflected across the line \(y=x\) to form the image \(A′B′C′D′\).
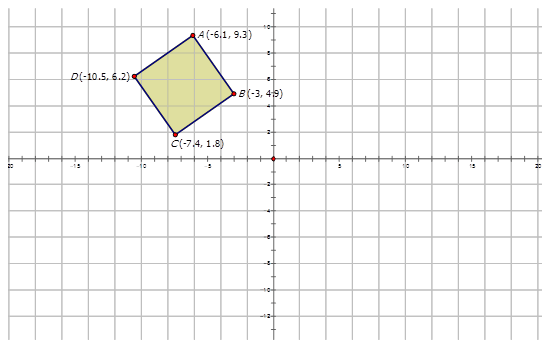
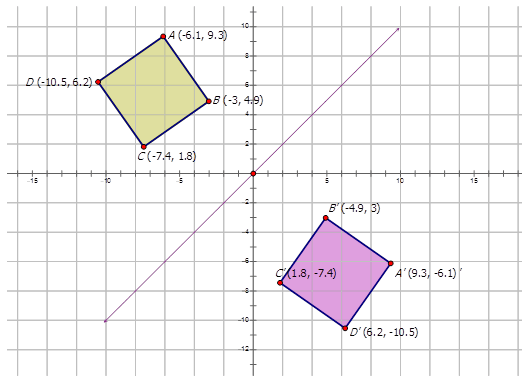
Example \(\PageIndex{1}\)
Earlier, you were given the coordinates of Triangle \(A\), \(E(−5,−5)\), \(F(2,−6)\), and \(G(−2,0)\), and asked to reflect the image across the \(y\)-axis. What are the coordinates of the reflected triangle?
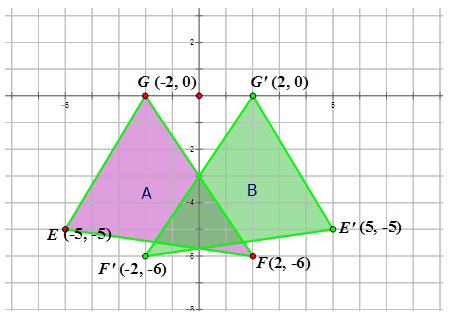
Solution
The coordinates of the new image (\(B\)) are \(E′(5,−5)\), \(F′(2,−6)\) and \(G′(2,0)\).
Example \(\PageIndex{2}\)
Line \(\overline{ST}\) drawn from \((-3, 4)\) to \((-3, 8)\) has been reflected across the line \(y=-x\). Draw the preimage and image and properly label each.
Solution
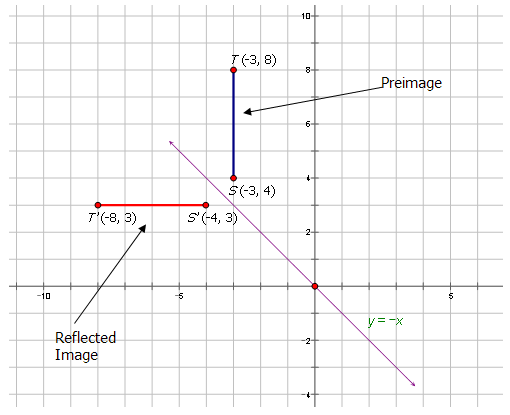
Example \(\PageIndex{3}\)
The polygon below has been reflected across the \(y\)-axis. Draw the reflected image and properly label each.
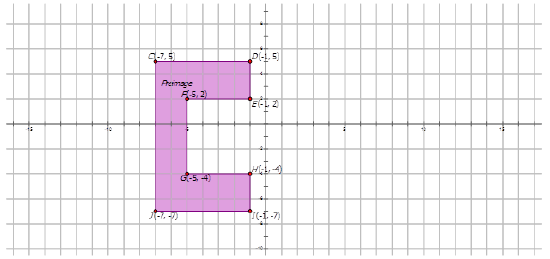
Solution
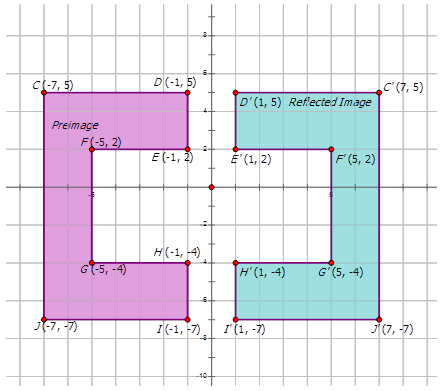
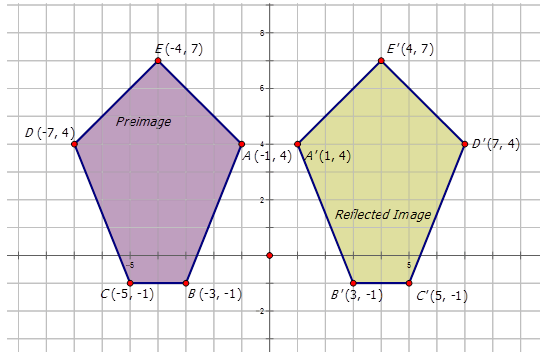
Example \(\PageIndex{4}\)
The purple pentagon is reflected across the \(y\)-axis to make the new image. Find the coordinates of the purple pentagon. On the diagram, draw and label the reflected pentagon.
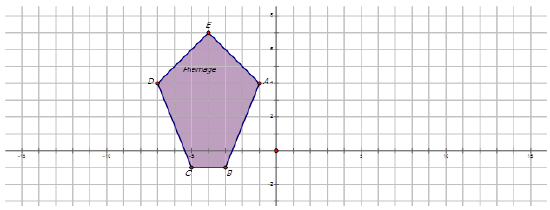
Solution
Reviews
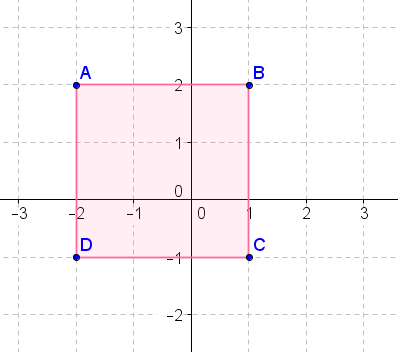
- Reflect the above figure across the \(x\)-axis.
- Reflect the above figure across the \(y\)-axis.
- Reflect the above figure across the line \(y=x\).
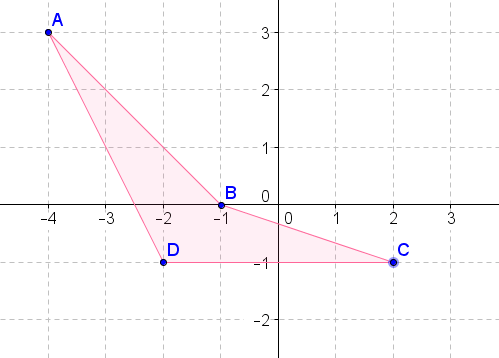
- Reflect the above figure across the \(x\)-axis.
- Reflect the above figure across the \(y\)-axis.
- Reflect the above figure across the line \(y=x\).
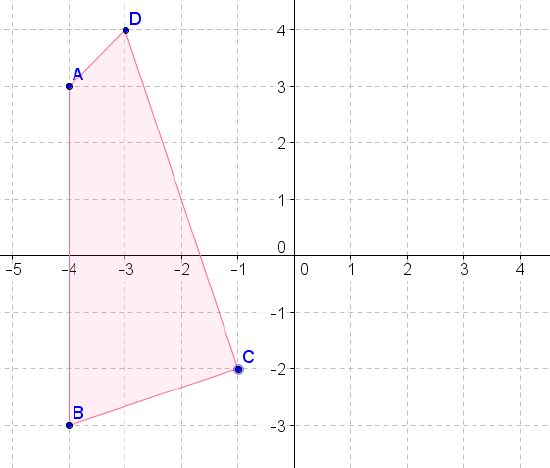
- Reflect the above figure across the \(x\)-axis.
- Reflect the above figure across the \(y\)-axis.
- Reflect the above figure across the line \(y=x\).
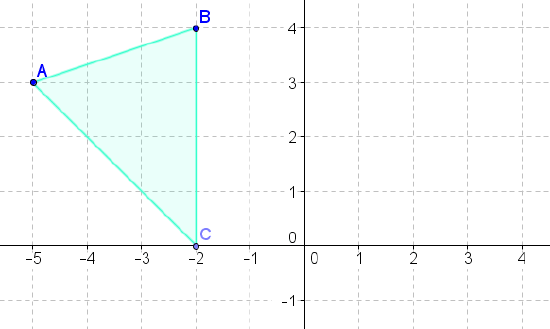
- Reflect the above figure across the \(x\)-axis.
- Reflect the above figure across the \(y\)-axis.
- Reflect the above figure across the line \(y=x\).
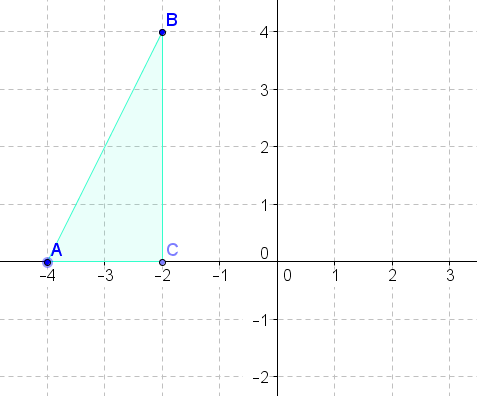
- Reflect the above figure across the \(x\)-axis.
- Reflect the above figure across the \(y\)-axis.
- Reflect the above figure across the line \(y=x\).
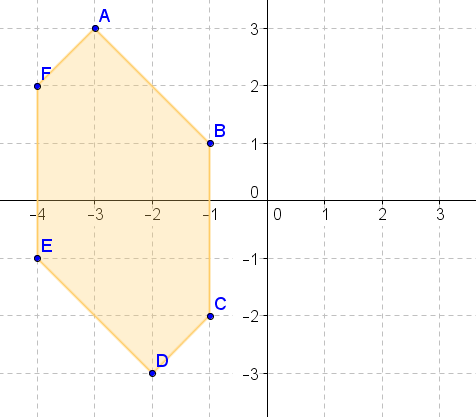
- Reflect the above figure across the \(x\)-axis.
- Reflect the above figure across the \(y\)-axis.
- Reflect the above figure across the line \(y=x\).
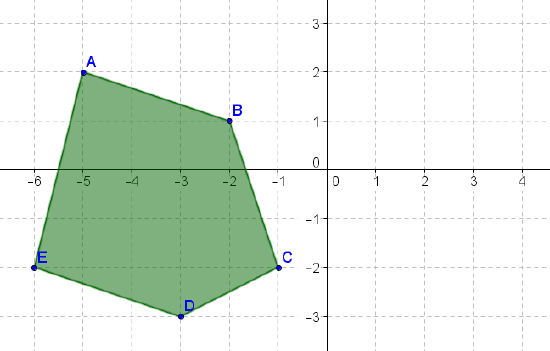
- Reflect the above figure across the \(x\)-axis.
- Reflect the above figure across the \(y\)-axis.
- Reflect the above figure across the line \(y=x\).
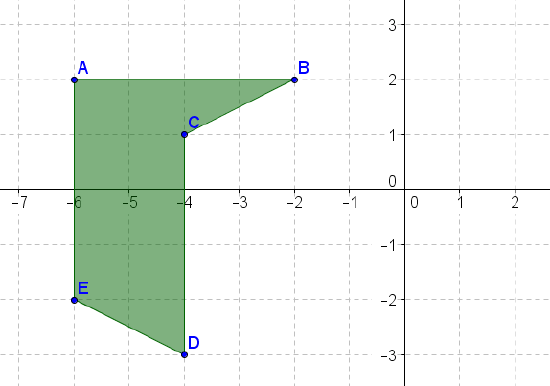
- Reflect the above figure across the \(x\)-axis.
- Reflect the above figure across the \(y\)-axis.
- Reflect the above figure across the line \(y=x\).
Review (Answers)
To see the Review answers, open this PDF file and look for section 10.5.
Additional Resources
Interactive Element
Practice: Geometry Software for Reflections