8.16: Reflecting Figures
- Page ID
- 6126
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Move figures on the coordinate plane using patterns.
Translations, Rotations, and Reflections
Tyler takes a picture of an item and its reflection. He places a coordinate plane over the picture. The coordinate plane is positioned so that the \(x\)−axis separates the image from the reflection. He then makes the grid according to the key features of the picture, so that a point at \((2, 0)\) is reflected at the point \((-2, 0)\). If the original coordinates of the image are \((3, 0)\), \((4, 6)\) and \((5, 1)\), what are the coordinates of the reflection?

In this concept, you will learn how to find the coordinates for translations, rotations and reflections.
Finding Coordinates for Translations, Rotations, and Reflections
When you perform translations, you slide a figure left or right, up or down. This means that on the coordinate plane, the coordinates for the vertices of the figure will change.
To graph a translation, perform the same change for each point.
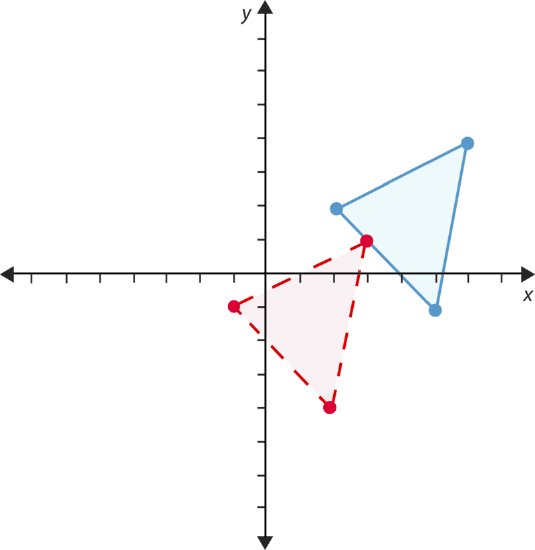
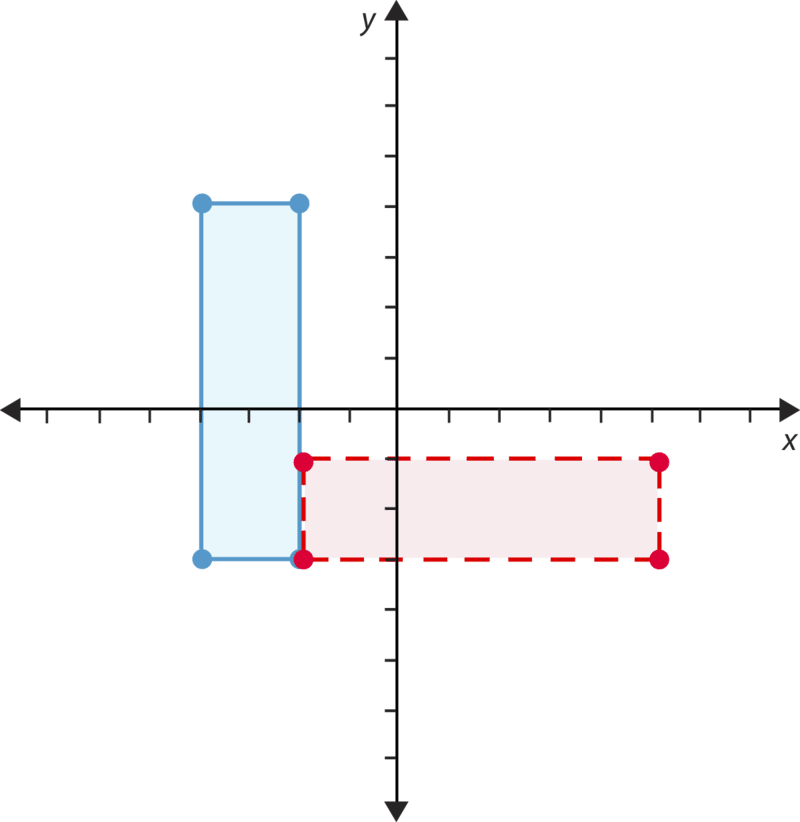
You can identify a reflection by the changes in its coordinates. In a reflection, the figure flips across a line to make a mirror image of itself. Take a look at the reflection below.
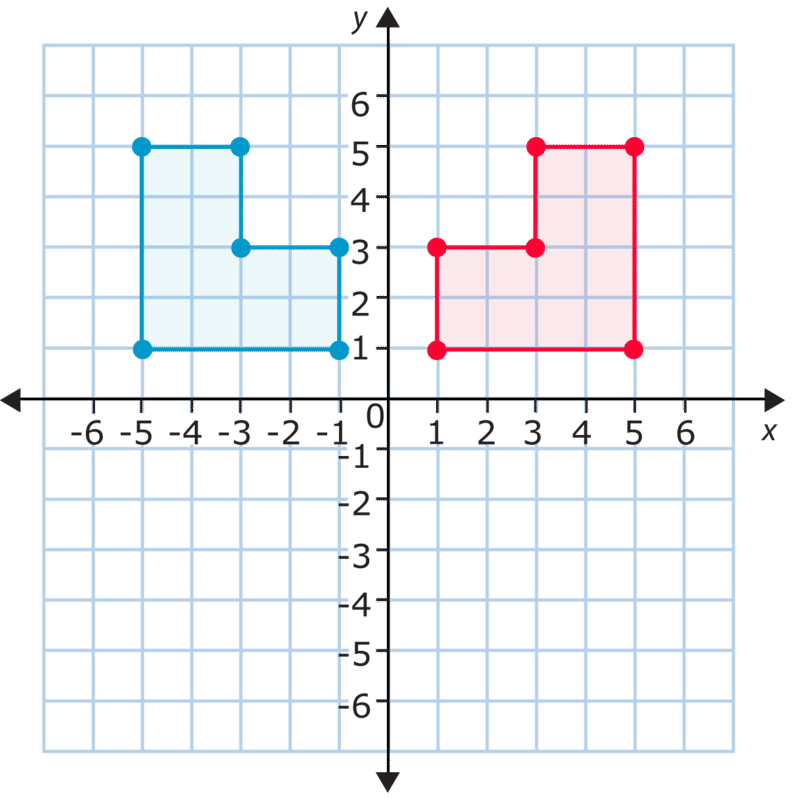
Figures are usually reflected across either the \(x\)− or the \(y\)-axis. In this case, the figure is reflected across the \(y\)-axis. If you compare the figures in the first example vertex by vertex, you see that the \(x\)−coordinates change but the \(y\)−coordinates stay the same. This is because the reflection happens from left to right across the \(y\)-axis. When you reflect across the \(x\)−axis, the \(y\)−coordinates change and the \(x\)−coordinates stay the same. Take a look at this example.
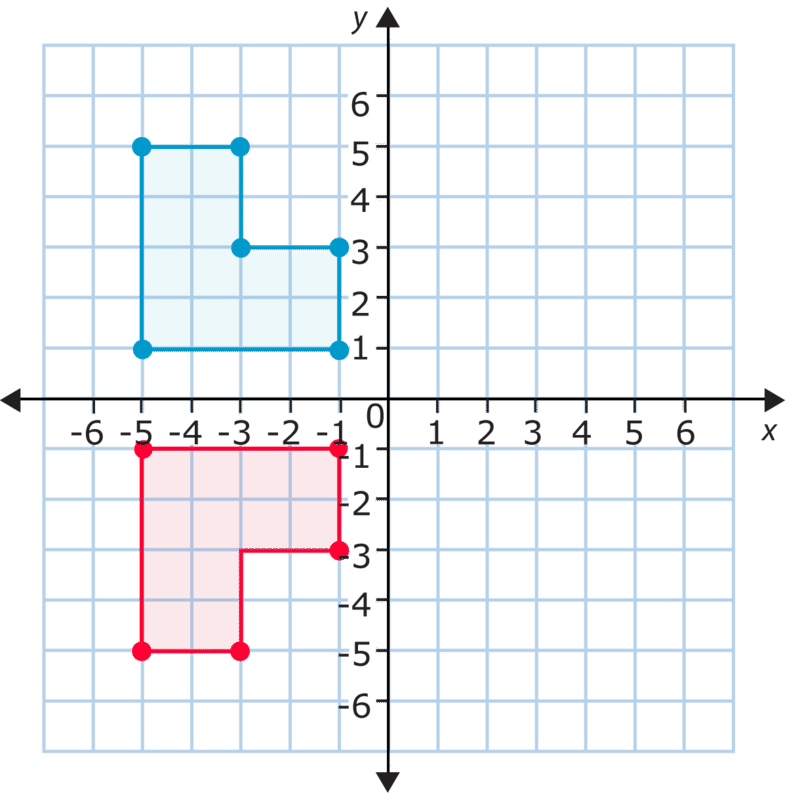
In the figure above the coordinates for the upper-left vertex of the original figure are \((-5, 5)\). After you reflect it across the \(x\)−axis, the coordinates for the corresponding vertex are \((-5, -5)\). How about the lower-right vertex? It starts out at \((-1, 1)\), and after the flip it is at \((-1, -1)\). As you can see, the \(x\)−coordinates stay the same while the \(y\)−coordinates change. In fact, the \(y\)−coordinates all become the opposite integers of the original \(y\)−coordinates. This indicates that this is a vertical (up/down) reflection or a reflection over the \(x\)−axis.
In a horizontal (left/right) reflection or a reflection over the \(y\)-axis, the \(x\)−coordinates would become integer opposites. Let’s look at an example.
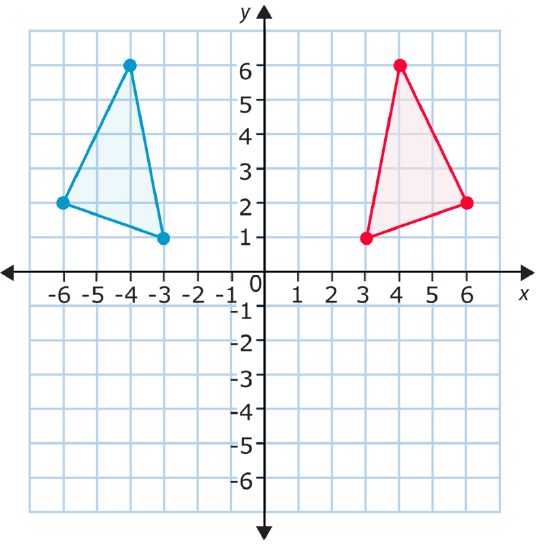
This is a reflection across the \(y\)-axis. Compare the points. Notice that the \(y\)−coordinates stay the same. The \(x\)−coordinates become the integer opposites of the original \(x\)−coordinates. Look at the top point of the triangle, for example. The coordinates of the original point are \((-4, 6)\), and the coordinates of the new point are \((4, 6)\). The \(x\)−coordinate has switched from -4 to 4.
You can recognize reflections by these changes to the \(x\)− and \(y\)−coordinates. If you reflect across the \(x\)−axis, the \(y\)−coordinates will become opposite. If you reflect across the \(y\)-axis, the \(x\)−coordinates will become opposite.
You can also use this information to graph reflections. To graph a reflection, you need to decide whether the reflection will be across the \(x\)−axis or the \(y\)-axis, and then change either the \(x\)− or \(y\)−coordinates.
Now let’s look at the third kind of transformation: rotations. A rotation is a transformation that turns the figure in either a clockwise or counterclockwise direction. The figure below has been rotated. What are its new coordinates?
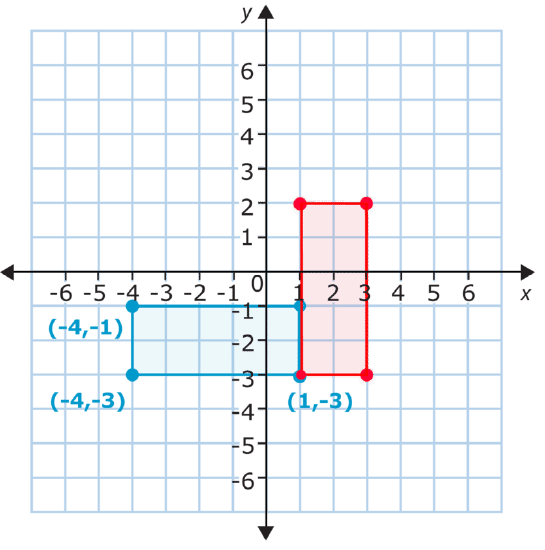
The new coordinates of the rectangle’s vertices are \((1, -3)\), \((1, 2)\), \((3, 2)\), and \((3, -3)\). As you can see, both the \(x\)− and \(y\)−coordinates changed. One of the points remained exactly the same. That means the figure was rotated about this point. Imagine you put your finger on this corner of the rectangle and spun it. That’s what happened in the rotation. The rectangle has been rotated \(90^{\circ}\) clockwise.
When you graph a rotation, you first need to know how much the figure will be rotated. Rotating the rectangle above \(90^{\circ}\) stands it up on end. Rotating it \(180^{\circ}\) would make it flat again. You also need to know which point you will rotate it around. This is the point that stays the same.
Next, you need to count how many units long and wide the figure is. The figure above stretches from 1 on the \(x\)−axis to -4 on the \(x\)−axis. This is a total of 5 units along the \(x\)−axis. When you rotate a figure \(90^{\circ}\), the distance on the \(x\)−axis becomes the distance on the \(y\)-axis. Look at the rectangle. The long sides are horizontal at first, but after you rotate it, they become the vertical sides. This means that the x−distance of 5 will become a y−distance of 5.
Now, remember the point \((1, -3)\) stays the same, so it is one corner of the rotated figure. You add 5 to the \(y\)−coordinate to find the next vertex of the rectangle. \(−3+5=2\). This puts a vertex at (1, 2)\).
To find the other points of the rotated rectangle, you need to think about its width. Find the width, or short side, of the original rectangle by counting the units between vertices along the \(y\)-axis. The rectangle covers 2 units on the \(y\)-axis. As you might guess, this becomes the \(x\)−distance in the rotated figure. In other words, you add 2 to the \(x\)−coordinate of the point that stays the same. \(1+2=3\), so another vertex of the rectangle will be \((3, -3)\). To find the fourth and final vertex, add 2 to the \(x\)−coordinate of the other ordered pair, \((1, 2)\). This puts the last vertex at \((3, 2)\).
Write each set of coordinates to show a reflection in the \(y\)-axis.
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Tyler and his picture.
If the original coordinates of the image are \((3, 0)\), \((4, 6)\) and \((5, 1)\), what are the coordinates of the reflection?
Solution
First, remember how to reflect across the \(x\)−axis.
Flip the shape across the \(x\)−axis.
Next, remember the rules.
The \(y\)−coordinates will change to their integer opposites.
Then, write the new points.
\((3, 0)\), \((4, -6)\), \((5, -1)\)
The answer is that the coordinates of the reflection are \((3, 0)\), \((4, -6)\), \((5, -1)\).
Example \(\PageIndex{2}\)
The figure below is reflected across the \(x\)−axis. What are the coordinates of the reflection?
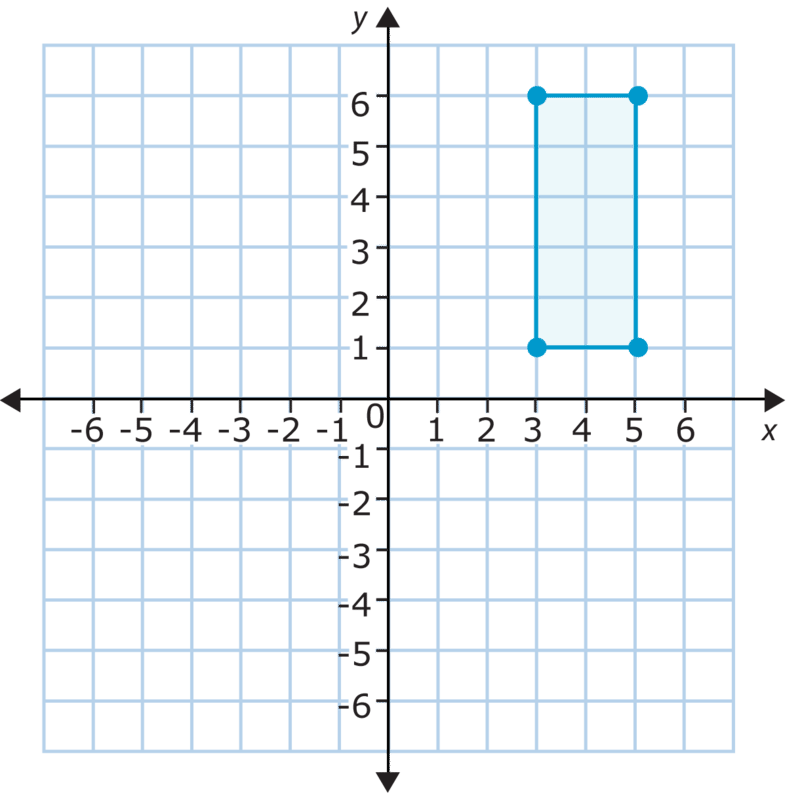
Solution
First, remember how to reflect across the \(x\)−axis.
Flip the shape across the \(x\)−axis.
Next, remember the rules.
The \(y\)−coordinates will change to their integer opposites.
Then, write the new points.
\((3, -6)\), \((3, -1)\), \((5, -6)\), \((5, -1)\)
The answer is that the coordinates of the reflection are \((3, -6)\), \((3, -1)\), \((5, -6)\), \((5, -1)\).
Example \(\PageIndex{3}\)
Determine if the change is the result of a translation, reflection or rotation.
After a transformation, the vertices \((3, 1)\), \((0, 3)\), \((1, 2)\) become \((3, -1)\), \((0, -3)\), \((1, -2)\).
Solution
First, look at the coordinates to see which coordinate changes.
The \(x\)−coordinates stay the same and the \(y\)−coordinates change for each of the points.
Next, determine the type of change for the coordinates.
The new \(y\)−coordinates are opposites of the original coordinates.
Then, state the type of transformation.
Reflection
The answer is that the change is the result of a reflection.
Example \(\PageIndex{4}\)
Determine if the change is the result of a translation, reflection or rotation.
After a transformation, the vertices \((-3, 6)\), \((-2, 3)\), \((2, 3)\), \((3, 6)\) become \((-3, -1)\), \((-2, 8)\), \((2, 8)\), \((3, 11)\).
Solution
First, look at the coordinates to see which coordinate changes.
The \(x\)−coordinates stay the same and the \(y\)−coordinates change for each of the points.
Next, determine the type of change for the coordinates.
The new \(y\)−coordinates are each 5 more than the original coordinates.
Then, state the type of transformation.
Translation
The answer is that the change is the result of a translation.
Example \(\PageIndex{5}\)
The points \((1, 2)\), \((3, 7)\), \((3, 4)\), \((5, 6)\) are reflected over the \(y\)-axis. What are the new coordinates?
Solution
First, remember the changes that occur with a reflection over the \(y\)-axis.
The \(x\)−coordinates become the opposite and the \(y\)−coordinates stay the same.
Then, write the new coordinates.
\((-1, 2)\), \((-3, 7)\), \((-3, 4)\), \((-5, 6)\)
The answer is that the new coordinates are \((-1, 2)\), \((-3, 7)\), \((-3, 4)\), \((-5, 6)\).
True or false. When there is a reflection in the \(y\)-axis, both coordinates change to opposites.
Review
Use this figure to answer each question. Be sure to write everything in coordinate notation when possible.
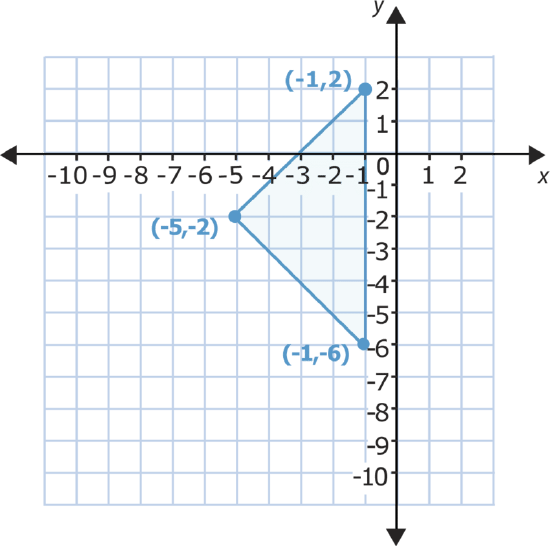
- Translate this figure three units up.
- Translate this figure four units to the right.
- Translate this figure five units down.
- Translate this figure six units to the left.
- Translate this figure one unit down and two units to the right.
- Translate this figure two units up and one unit to the left.
- Translate this figure three units up and one unit to the right.
- Rotate this figure 180 degrees.
- Rotate this figure 90 degrees.
- Reflect this figure over the x axis.
- Reflect this figure over the y axis.
- Translate this figure five units up and three units to the right.
- Translate this figure six units down and four units to the left.
- True or false. The figure below is an image of a reflection.
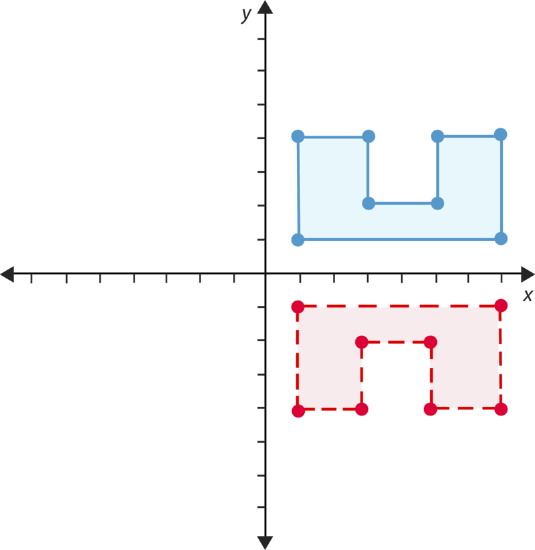
- True or false. This figure has been rotated \(180^{\circ}\).
Review (Answers)
To see the Review answers, open this PDF file and look for section 8.19.
Resources
Vocabulary
| Term | Definition |
|---|---|
| \(x\)−axis | The \(x\)−axis is the horizontal axis in the coordinate plane, commonly representing the value of the input or independent variable. |
| \(y\)-axis | The \(y\)-axis is the vertical number line of the Cartesian plane. |
| Coordinate Notation | A coordinate point is the description of a location on the coordinate plane. Coordinate points are commonly written in the form \((x, y)\) where \(x\) is the horizontal distance from the origin, and y is the vertical distance from the origin. |
| Coordinate Plane | The coordinate plane is a grid formed by a horizontal number line and a vertical number line that cross at the \((0, 0)\) point, called the origin. The coordinate plane is also called a Cartesian Plane. |
| Reflection | A reflection is a transformation that flips a figure on the coordinate plane across a given line without changing the shape or size of the figure. |
| Rotation | A rotation is a transformation that turns a figure on the coordinate plane a certain number of degrees about a given point without changing the shape or size of the figure. |
| Transformation | A transformation moves a figure in some way on the coordinate plane. |
| Translation | A translation is a transformation that slides a figure on the coordinate plane without changing its shape, size, or orientation. |
Additional Resources
Interactive Element
Practice: Reflecting Figures
Real World: Mirror, Mirror

