8.17: Composite Transformations
- Page ID
- 6154
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learn how to compose transformations of a figure on a coordinate plane, and understand the order in which to apply them.
Transformations Summary
A transformation is an operation that moves, flips, or otherwise changes a figure to create a new figure. A rigid transformation (also known as an isometry or congruence transformation) is a transformation that does not change the size or shape of a figure. The new figure created by a transformation is called the image. The original figure is called the preimage.
There are three rigid transformations: translations, rotations and reflections. A translation is a transformation that moves every point in a figure the same distance in the same direction. A rotation is a transformation where a figure is turned around a fixed point to create an image. A reflection is a transformation that turns a figure into its mirror image by flipping it over a line.
Composition of Transformations
A composition (of transformations) is when more than one transformation is performed on a figure. Compositions can always be written as one rule. You can compose any transformations, but here are some of the most common compositions:
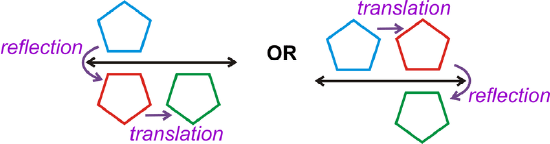
- A glide reflection is a composition of a reflection and a translation. The translation is in a direction parallel to the line of reflection.
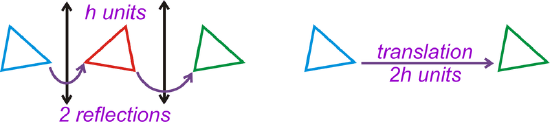
- The composition of two reflections over parallel lines that are \(h\) units apart is the same as a translation of \(2h\) units (Reflections over Parallel Lines Theorem).
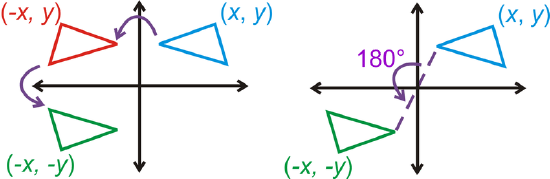
If you compose two reflections over each axis, then the final image is a rotation of \(180^{\circ}\) around the origin of the original (Reflection over the Axes Theorem).
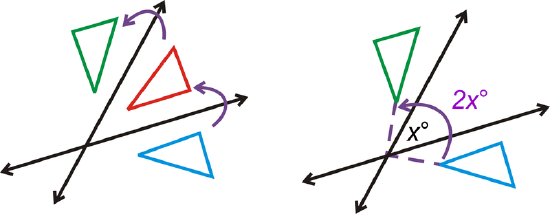
A composition of two reflections over lines that intersect at \(x^{\circ}\) is the same as a rotation of \(2x^{\circ}\). The center of rotation is the point of intersection of the two lines of reflection (Reflection over Intersecting Lines Theorem).
What if you were given the coordinates of a quadrilateral and you were asked to reflect the quadrilateral and then translate it? What would its new coordinates be?
Example \(\PageIndex{1}\)
Reflect \(\Delta ABC\) over the \(y\)-axis and then translate the image 8 units down.
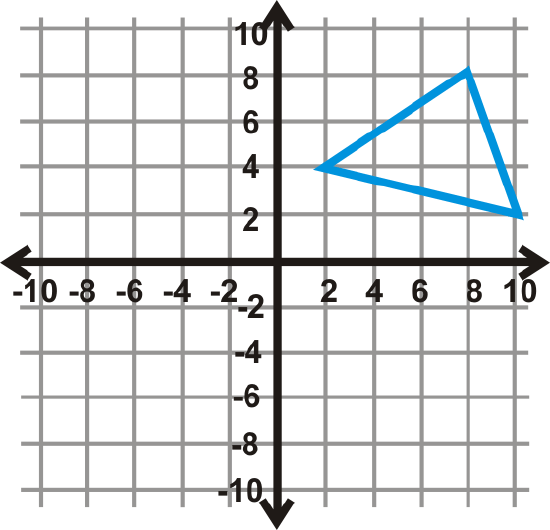
Solution
The green image to the left is the final answer.
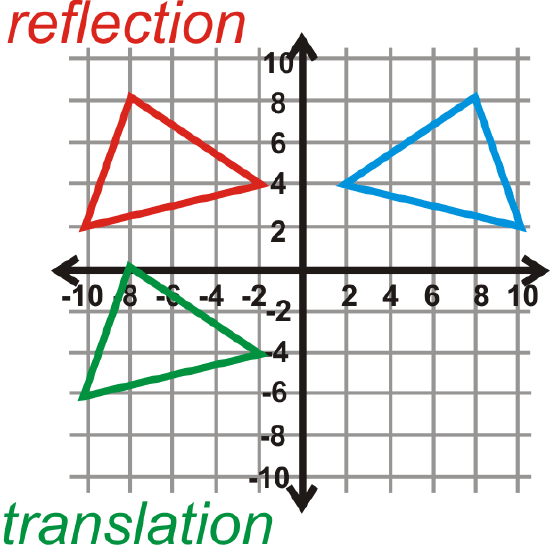
\(\begin{aligned} A(8,8)&\rightarrow A′′(−8,0) \\ B(2,4)&\rightarrow B′′(−2,−4) \\ C(10,2)&\rightarrow C′′(−10,−6) \end{aligned}\)
Example \(\PageIndex{2}\)
Write a single rule for \(\Delta ABC\) to \(\Delta A′′B′′C′′\) from Example 1.
Solution
Looking at the coordinates of \(A\) to \(A′′\), the \(x\)−value is the opposite sign and the \(y\)−value is \(y−8\). Therefore the rule would be \((x,y)\rightarrow (−x,y−8)\).
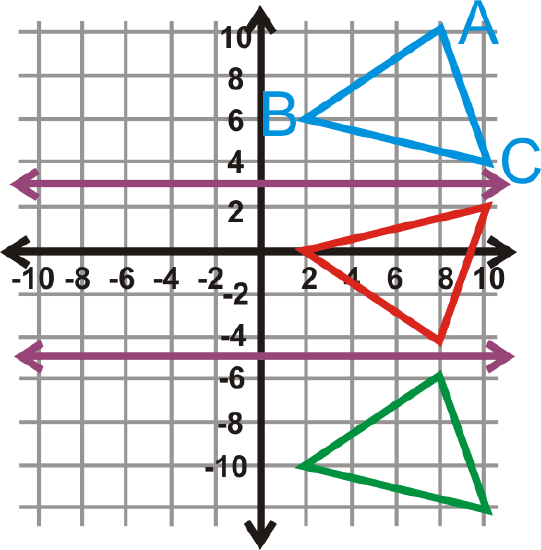
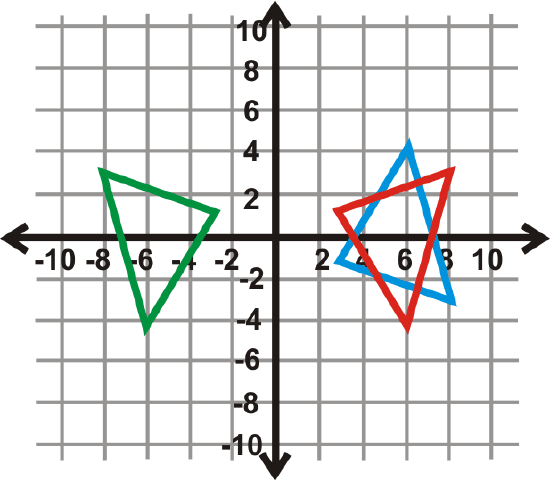
Example \(\PageIndex{3}\)
Reflect \(\Delta ABC\) over \(y=3\) and then reflect the image over \(y=−5\).
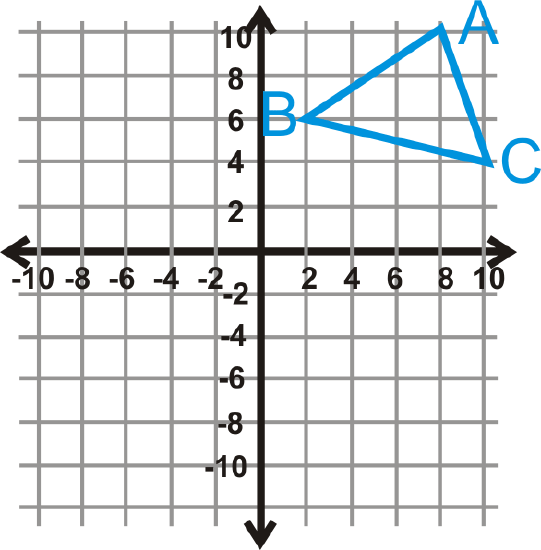
Solution
Order matters, so you would reflect over \(y=3\) first, (red triangle) then reflect it over \(y=−5\) (green triangle).
Example \(\PageIndex{4}\)
A square is reflected over two lines that intersect at a \(79^{\circ}\) angle. What one transformation will this be the same as?
Solution
From the Reflection over Intersecting Lines Theorem, this is the same as a rotation of \(2\cdot 79^{\circ}\)=178^{\circ}\).
Example \(\PageIndex{5}\)
\(\Delta DEF\) has vertices \(D(3,−1)\), \(E(8,−3)\), and \(F(6,4)\). Reflect \(\Delta DEF\) over \(x=−5\) and then \(x=1\). Determine which one translation this double reflection would be the same as.
Solution
From the Reflections over Parallel Lines Theorem, we know that this double reflection is going to be the same as a single translation of \(2(1−(−5))\) or 12 units.
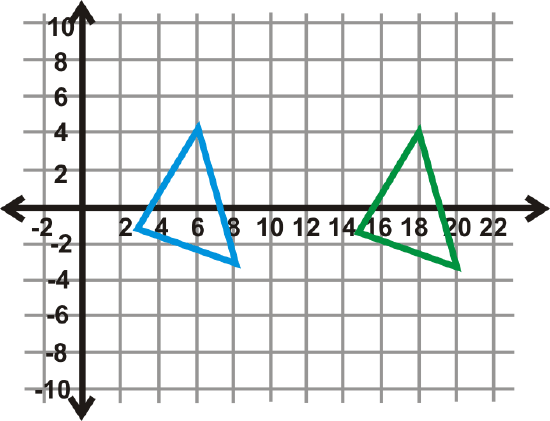
Example \(\PageIndex{6}\)
Reflect \(\Delta DEF\) from Question 2 over the \(x\)-axis, followed by the \(y\)-axis. Find the coordinates of \(\Delta D′′E′′F′′\) and the one transformation this double reflection is the same as.
Solution
\(\Delta D′′E′′F′′\) is the green triangle in the graph to the left. If we compare the coordinates of it to \(\Delta DEF\), we have:
\(\begin{aligned}D(3,−1)&\rightarrow D′′(−3,1) \\ E(8,−3)&\rightarrow E′′(−8,3) \\ F(6,4)&\rightarrow F′′(−6,−4)\end{aligned}\)
Review
- Explain why the composition of two or more isometries must also be an isometry.
- What one transformation is the same as a reflection over two parallel lines?
- What one transformation is the same as a reflection over two intersecting lines?
Use the graph of the square to the left to answer questions 4-6.
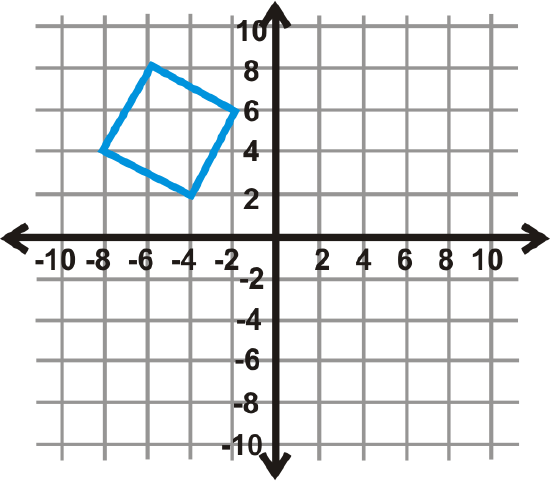
- Perform a glide reflection over the \(x\)-axis and to the right 6 units. Write the new coordinates.
- What is the rule for this glide reflection?
- What glide reflection would move the image back to the preimage?
Use the graph of the square to the left to answer questions 7-9.

- Perform a glide reflection to the right 6 units, then over the \(x\)-axis. Write the new coordinates.
- What is the rule for this glide reflection?
- Is the rule in #8 different than the rule in #5? Why or why not?
Use the graph of the triangle to the left to answer questions 10-12.
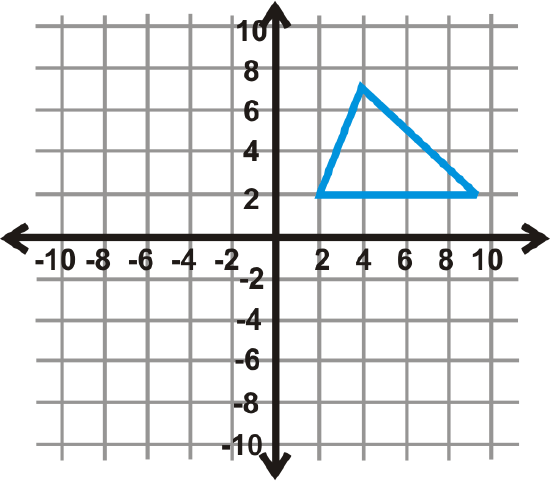
- Perform a glide reflection over the \(y\)-axis and down 5 units. Write the new coordinates.
- What is the rule for this glide reflection?
- What glide reflection would move the image back to the preimage?
Use the graph of the triangle to the left to answer questions 13-15.
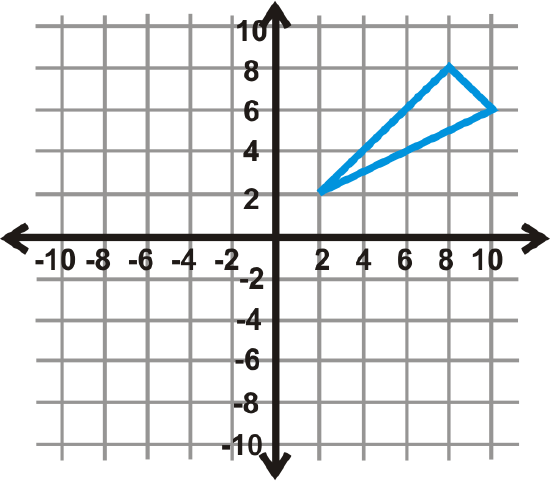
- Reflect the preimage over \(y=−1\) followed by \(y=−7\). Draw the new triangle.
- What one transformation is this double reflection the same as?
- Write the rule.
Use the graph of the triangle to the left to answer questions 16-18.

- Reflect the preimage over \(y=−7\) followed by \(y=−1\). Draw the new triangle.
- What one transformation is this double reflection the same as?
- Write the rule.
- How do the final triangles in #13 and #16 differ?
Use the trapezoid in the graph to the left to answer questions 20-22.
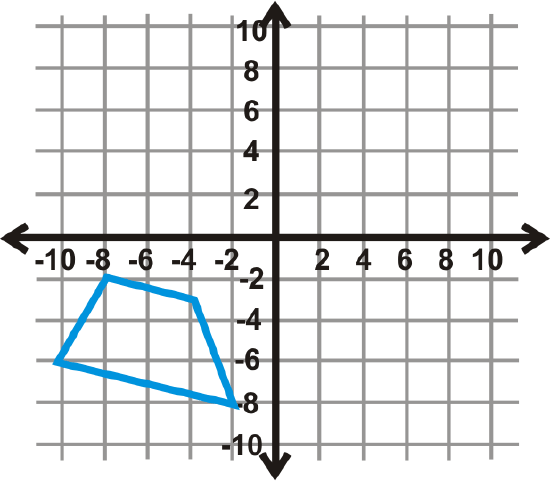
- Reflect the preimage over the \(x\)-axis then the \(y\)-axis. Draw the new trapezoid.
- Now, start over. Reflect the trapezoid over the \(y\)-axis then the \(x\)-axis. Draw this trapezoid.
- Are the final trapezoids from #20 and #21 different? Why do you think that is?
Answer the questions below. Be as specific as you can.
- Two parallel lines are 7 units apart. If you reflect a figure over both how far apart with the preimage and final image be?
- After a double reflection over parallel lines, a preimage and its image are 28 units apart. How far apart are the parallel lines?
- Two lines intersect at a \(165^{\circ}\) angle. If a figure is reflected over both lines, how far apart will the preimage and image be?
- What is the center of rotation for #25?
- Two lines intersect at an \(83^{\circ}\) angle. If a figure is reflected over both lines, how far apart will the preimage and image be?
- A preimage and its image are \(244^{\circ}\) apart. If the preimage was reflected over two intersecting lines, at what angle did they intersect?
- A preimage and its image are \(98^{\circ}\) apart. If the preimage was reflected over two intersecting lines, at what angle did they intersect?
- After a double reflection over parallel lines, a preimage and its image are 62 units apart. How far apart are the parallel lines?
Review (Answers)
To see the Review answers, open this PDF file and look for section 12.6.
Vocabulary
| Term | Definition |
|---|---|
| composition (of transformations) | When more than one transformation is performed on a figure. |
| Rotation | A rotation is a transformation that turns a figure on the coordinate plane a certain number of degrees about a given point without changing the shape or size of the figure. |
| Reflection | A reflection is a transformation that flips a figure on the coordinate plane across a given line without changing the shape or size of the figure. |
| Glide Reflection | A reflection followed by a translation where the line of reflection is parallel to the direction of translation is called a glide reflection or a walk. |
| Composite Transformation | A composite transformation, also known as composition of transformation, is a series of multiple transformations performed one after the other. |
Additional Resources
Interactive Element
Video: Composing Transformations Principles - Basic
Activities: Composition of Transformations Discussion Questions
Study Aids: Composition of Transformations Study Guide
Practice: Composite Transformations

