8.18: Notation for Composite Transformations

Interpret and use notation for combined transformations

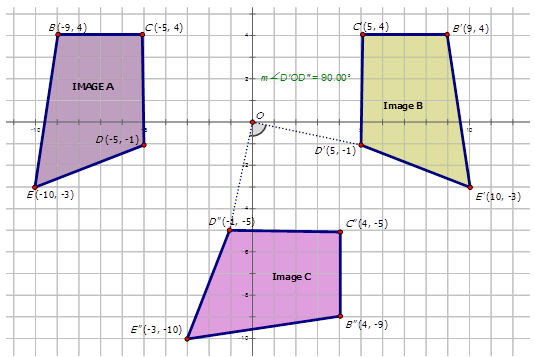
The figure below shows a composite transformation of a trapezoid. Write the mapping rule for the composite transformation.

Figure $\PageIndex{1}$

In geometry, a transformation is an operation that moves, flips, or changes a shape to create a new shape. A composite transformation is when two or more transformations are performed on a figure (called the preimage) to produce a new figure (called the image). The order of transformations performed in a composite transformation matters.

To describe a composite transformation using notation, state each of the transformations that make up the composite transformation and link them with the symbol $\circ$. The transformations are performed in order from right to left. Recall the following notation for translations, reflections, and rotations:

• Translation: $T_{a,b}: (x,y)\rightarrow (x+a,y+b)$ is a translation of $a$ units to the right and $b$ units up.
• Reflection: $r_{y−axis}(x,y)\rightarrow (−x,y)$.
• Rotation: $R_{90^{\circ}}(x,y)=(−y,x)$

Let's graph the line described below and the composite image defined by $r_{y−axis} \circ R_{90^{\circ}}$:

The first translation is a $90^{\circ}$ CCW turn about the origin to produce $X′Y′$. The second translation is a reflection about the $y$-axis to produce $X′′Y′′$.

Figure $\PageIndex{2}$

Now, let's graph the composite images described in the following problems:

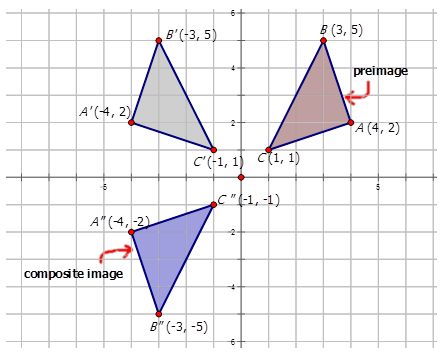
1. Image A with vertices $A(3,5)$, $B(4,2)$ and $C(1,1)$ undergoes a composite transformation with mapping rule $r_{x−axis} \circ r_{y−axis}$.

Figure $\PageIndex{3}$

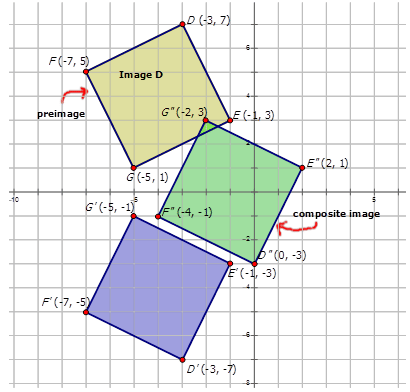
2. Image $D$ with vertices $D(−3,7)$, $E(−1,3)$, $F(−7,5)$ and $G(−5,1)$ undergoes a composite transformation with mapping rule $T_{3,4} \circ r_{x−axis}$.

Figure $\PageIndex{4}$

Example $\PageIndex{1}$

Earlier, you were asked to write the mapping rule for the following composite transformation:

Figure $\PageIndex{5}$

Solution

The transformation from Image $A$ to Image $B$ is a reflection across the $y$-axis. The notation for this is $r_{y−axis}$. The transformation for image B to form image $C$ is a rotation about the origin of $90^{\circ}CW$. The notation for this transformation is $R_{270^{\circ}}$. Therefore, the notation to describe the transformation of Image $A$ to Image $C$ is $R_{270^{\circ}} \circ r_{y−axis}$

Example $\PageIndex{2}$

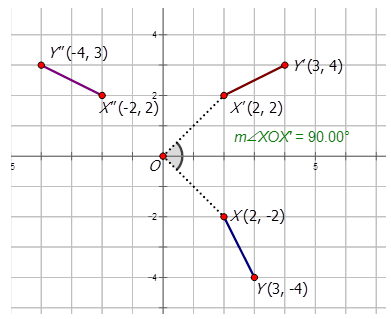
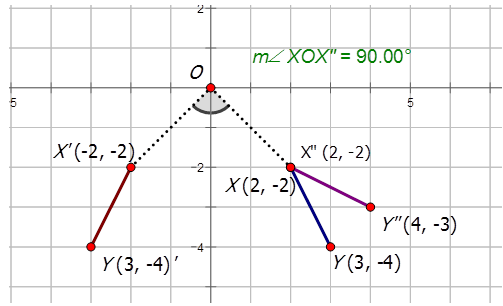
Graph the line $XY$ given that $X(2,−2)$ and $Y(3,−4)$. Also graph the composite image that satisfies the rule $R_{90^{\circ}} \circ r_{y−axis}$

Solution

The first transformation is a reflection about the $y$-axis to produce $X′Y′$. The second transformation is a $90^{\circ}CCW$ turn about the origin to produce $X′′Y′′$.

Figure $\PageIndex{6}$

Example $\PageIndex{3}$

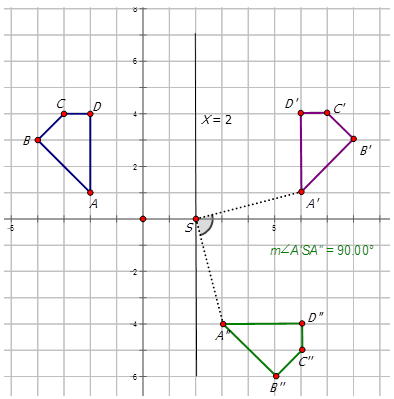
Describe the composite transformations in the diagram below and write the notation to represent the transformation of figure $ABCD$ to $A′′B′′C′′D′′$.

Figure $\PageIndex{7}$

Solution

There are two transformations shown in the diagram. The first transformation is a reflection about the line X=2\) to produce $A′B′C′D′$. The second transformation is a $90^{\circ}$CW (or $270^{\circ}CCW$) rotation about the point $(2, 0)$ to produce the figure $A′′B′′C′′D′′$. Notation for this composite transformation is:

$R_{270^{\circ}} \circ r_{x=2}$

Example $\PageIndex{4}$

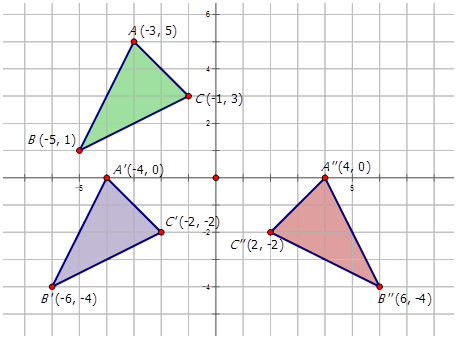
Describe the composite transformations in the diagram below and write the notation to represent the transformation of figure $ABC$ to $A′′B′′C′′$.

Figure $\PageIndex{8}$

Solution

There are two transformations shown in the diagram. The first transformation is a translation of 1 unit to the left and 5 units down to produce $A′B′C′$. The second reflection in the $y$-axis to produce the figure $A′′B′′C′′$. Notation for this composite transformation is:

$r_{y−axis} \circ T_{−1,−5}$

Review

Complete the following table:

Starting Point	$T_{3,−4} \circ R_{90^{\circ}}$	$r_{x−axis} \circ r_{y−axis}$	$T_{1,6} \circ r_{x-axis}$	$r_{y−axis} \circ R_{180^{\circ}}$
1. $(1, 4)$
2. $(4, 2)$
3. $(2, 0)$
4. $(-1, 2)$
5. $(-2, -3)$
6. $(4, -1)$
7. $(3, -2)$
8. $(5, 4)$
9. $(-3, 7)$
10. $(0, 0)$

Write the notation that represents the composite transformation of the preimage $A$ to the composite images in the diagrams below.

11. 

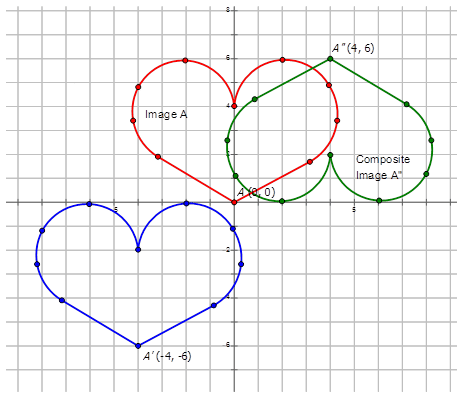
    Figure $\PageIndex{9}$

12. 

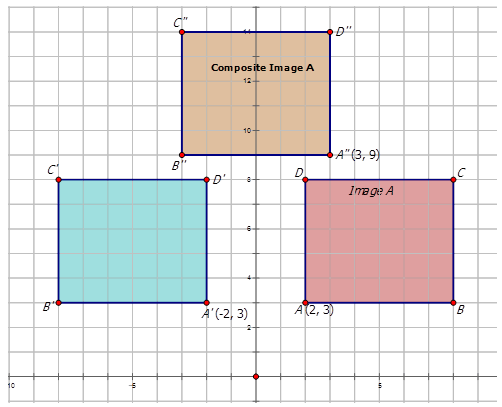
    Figure $\PageIndex{10}$

13. 

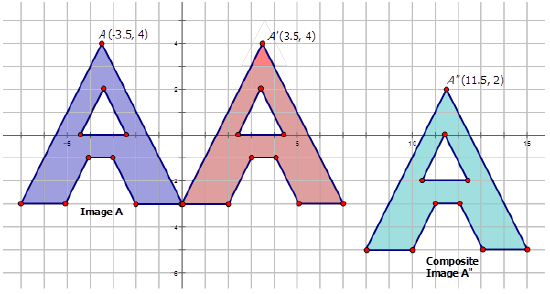
    Figure $\PageIndex{11}$

14. 

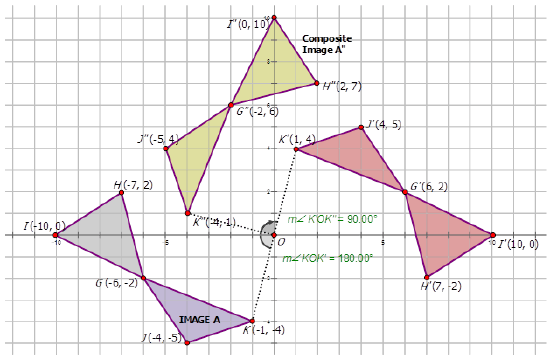
    Figure $\PageIndex{12}$

15. 

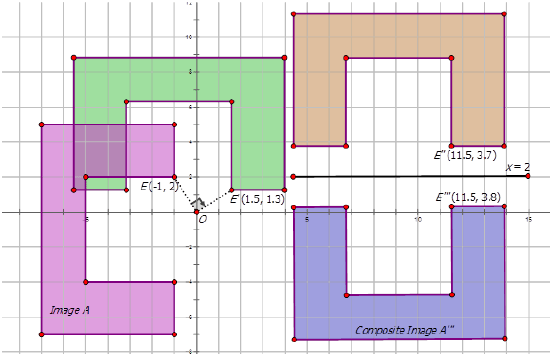
    Figure $\PageIndex{13}$

Review (Answers)

To see the Review answers, open this PDF file and look for section 10.15.

Vocabulary

Term	Definition
Reflections	Reflections are transformations that result in a "mirror image" of a parent function. They are caused by differing signs between parent and child functions.
Rotation	A rotation is a transformation that turns a figure on the coordinate plane a certain number of degrees about a given point without changing the shape or size of the figure.
Transformation	A transformation moves a figure in some way on the coordinate plane.

Additional Resources

Practice: Notation for Composite Transformations