8.19: Tessellations
- Page ID
- 6156
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Tiling over a plane such that the figures fill the plane with no overlaps or gaps.
A tessellation is a tiling over a plane with one or more figures such that the figures fill the plane with no overlaps and no gaps. You have probably seen tessellations before. Examples of a tessellation are: a tile floor, a brick or block wall, a checker or chess board, and a fabric pattern. The following pictures are also examples of tessellations.
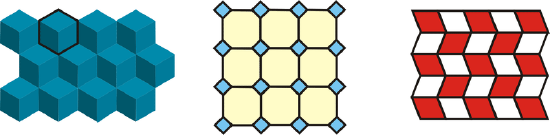
Notice the hexagon (cubes, first tessellation) and the quadrilaterals fit together perfectly. If we keep adding more, they will entirely cover the plane with no gaps or overlaps.
We are only going to worry about tessellating regular polygons. To tessellate a shape, it must be able to exactly surround a point, or the sum of the angles around each point in a tessellation must be \(360^{\circ}\). The only regular polygons with this feature are equilateral triangles, squares, and regular hexagons.
What if you were given a hexagon and asked to tile it over a plane such that it would fill the plane with no overlaps and no gaps?
Example \(\PageIndex{1}\)
How many regular hexagons will fit around one point?
Solution
First, recall how many degrees are in a circle, and then figure out how many degrees are in each angle of a regular hexagon. There are \(360^{\circ}\) in a circle and \(120^{\circ}\) in each interior angle of a hexagon, so \(\dfrac{360}{120}=3\) hexagons will fit around one point.
Example \(\PageIndex{2}\)
Does a regular octagon tessellate?
Solution
First, recall that there are \(1080^{\circ}\) in a pentagon. Each angle in a regular pentagon is \(1080^{\circ}\divide 8=135^{\circ}\). From this, we know that a regular octagon will not tessellate by itself because \(135^{\circ}\) does not go evenly into \(360^{\circ}\).
Example \(\PageIndex{3}\)
Draw a tessellation of equilateral triangles.
Solution
In an equilateral triangle each angle is \(60^{\circ}\). Therefore, six triangles will perfectly fit around each point.
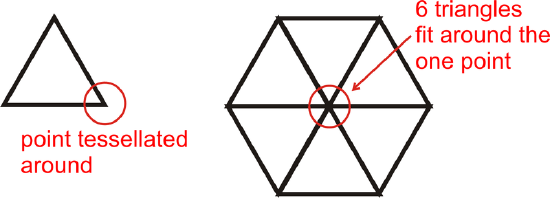
Extending the pattern, we have:
Example \(\PageIndex{4}\)
Does a regular pentagon tessellate?
Solution
First, recall that there are \(540^{\circ}\) in a pentagon. Each angle in a regular pentagon is \(540^{\circ}\divide 5=108^{\circ}\). From this, we know that a regular pentagon will not tessellate by itself because \(108^{\circ}\) times 2 or 3 does not equal \(360^{\circ}\).
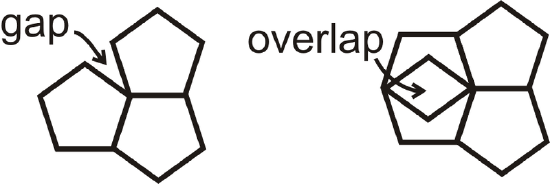
Example \(\PageIndex{5}\)
How many squares will fit around one point?
Solution
First, recall how many degrees are in a circle, and then figure out how many degrees are in each angle of a square. There are \(360^{\circ}\) in a circle and \(90^{\circ}\) in each interior angle of a square, so \(\dfrac{360}{90}=4\) squares will fit around one point.
Review
- Tessellate a square. Add color to your design.
- What is an example of a tessellated square in real life?
- Tessellate a regular hexagon. Add color to your design.
- You can also tessellate two regular polygons together. Try tessellating a regular hexagon and an equilateral triangle. First, determine how many of each fit around a point and then repeat the pattern. Add color to your design.
- Does a regular dodecagon (12-sided shape) tessellate? Why of why not?
- Does a kite tessellate? Why or why not?
Do the following figures tessellate?
-
Figure \(\PageIndex{5}\) -
Figure \(\PageIndex{6}\) -
Figure \(\PageIndex{7}\) -
Figure \(\PageIndex{8}\) -
Figure \(\PageIndex{9}\)\ -
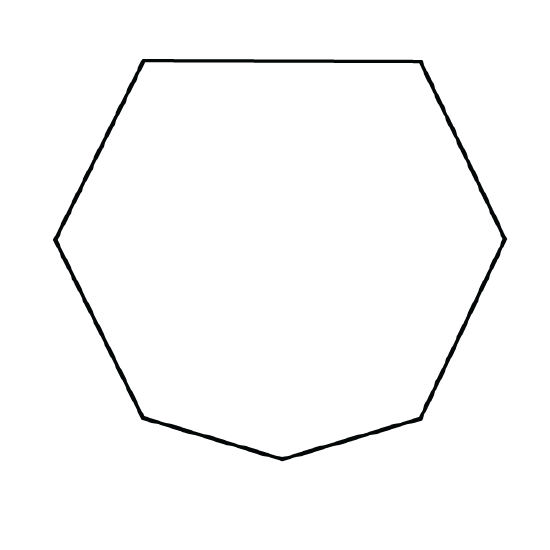
Figure \(\PageIndex{10}\) -
Figure \(\PageIndex{11}\) -
Figure \(\PageIndex{12}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 12.7.
Vocabulary
| Term | Definition |
|---|---|
| tessellation | A tiling over a plane with one or more figures such that the figures fill the plane with no overlaps and no gaps. |
| line segment | A line segment is a part of a line that has two endpoints. |
Additional Resources
Interactive Element
Video: Tessellations Principles - Basic
Activities: Symmetry and Tessellations Study Guide
Practice: Tessellations
Real World: The Master of Tessellations