9.9: Surface Area and Volume Applications
- Page ID
- 6197
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Use geometric solids to model real world objects and solve problems. Find density by the ratio of mass, people, or things to volume or area.
Modeling in Three Dimensions
Mark wants to make an open box from an 8.5 inch by 11 inch piece of paper by cutting squares out of each corner, folding up the sides, and securing with tape. How does the volume of his box relate to the size of the squares he cuts out?
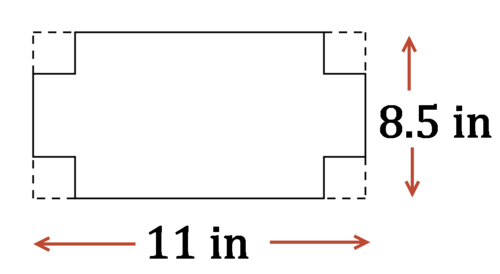
Modeling in Three Dimensions
You live in a three dimensional world. Look around and observe what you see over the course of your day. Can you find examples of prisms? Cylinders? Pyramids? Cones? Spheres?
While most objects in your daily life are not perfect prisms, pyramids, cylinders, cones, or spheres, most are close to one of these five solids or a combination of these solids. Modeling in three dimensions is about being able to choose the best solid to help analyze a real world three dimensional situation, and then using your geometry knowledge to make decisions about the real life situation. You should ask yourself:
- What solid or solids are the best model of this real life object?
- What problems am I trying to solve or decisions am I trying to make about the real life object?
- What information about the real life object am I given and where does it fit in my model?
Real-World Application: Chopping Trees
A big storm causes a large tree to fall in your yard. The main portion of the tree trunk measures about 9 feet around and is 40 feet long. You plan to chop up the tree to use and sell as fire wood. Approximately what volume of wood will you get from the tree?
A tree trunk is best modeled by a cylinder. Here, you are looking for the approximate volume of the cylinder. Two pieces of information are given.
1. “The main portion of the tree trunk measures about 9 feet around” --- This is the circumference of the base of the cylinder. You can use this measurement to find the radius of the cylinder.
\(2\pi r=9\rightarrow r=\dfrac{9}{2\pi} \rightarrow r\approx 1.43\text{ ft}\)
2. “40 feet long” --- This is the height of the cylinder.
\(h=40\text{ ft}\)
The volume of the wood from the tree is approximately:
\(V=\pi r^{2}h=\pi (1.43^{2})(40)\approx 257\text{ ft}^{3}\)
Real-World Application: Buying Wood
Wood is commonly sold in cords. A cord of wood is a stack of tightly packed wood that measures 4 feet by 4 feet by 8 feet. Approximately how many cords of wood will the chopped tree from the first problem produce?
A cord of wood is best modeled by a rectangular prism. \(V=A_{Base}\cdot h\), so \(V=(4\cdot 4)\cdot 8=128 ft^{3}\). Each cord of wood is approximately 128 cubic feet of wood. Since the tree from the first problem produced 257 cubic feet of wood, this is \(\dfrac{257}{128}\approx 2\) cords of wood.
Now, let's come up with an equation that relates the length around a tree in feet, the height of a tree in feet, and the approximate number of cords of wood that a tree will produce.
You want to come up with an equation that takes an input of circumference and height and produces an output of cords of wood. Think back to the steps taken in Examples A and B and repeat these steps with variables for circumference and height instead of specific values.
- Let \(C= \text{ distance around the tree}\)
- Let \(h= \text{ height of tree}\)
Use the distance around the tree to find the radius:
\(C=2\pi r\rightarrow r=C^2\pi\)
The volume of the wood from the tree is:
\(\begin{aligned} V&=\pi r^{2}h \\ &=\pi (\dfrac{C}{2\pi})^{2}h \\ &=\dfrac{C^{2}h}{4\pi}\end{aligned}\)
Once you have the volume of the wood from a given tree, to find the number of cords of wood divide the volume by 128 ft3, which is the number of cubic feet in a cord of wood.
\(\text{Number of Cords}=\dfrac{V}{128}=\dfrac{\dfrac{C^{2}h}{4\pi }}{128}=\dfrac{C^{2}h}{512\pi}\)
Test this formula using the original information from the first problem about chopping trees to see if you get the correct answer to the second problem. In this first problem, C=9 ft and h=40 ft.
\(\text{Number of Cords}=\dfrac{C^{2}h}{512\pi }=\dfrac{(9^{2})(40)}{512\pi }\approx 2.01\)
This matches the answer to , so you can feel confident that your equation is correct.
Example \(\PageIndex{1}\)
Earlier, you were asked how the volume of Mark's box relate to the size of the squares he cut out.
Solution
Let the length of the side of the square that Mark cuts out of each corner be x. The portion of the paper that will become the base of the box once it is made is shaded below in red.
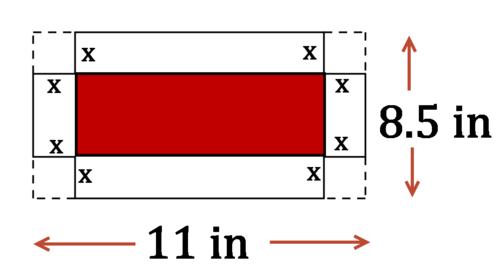
The box is a rectangular prism. The volume of the box is therefore \(V=A_{Base}\cdot h.
- \(A_{Base}=(11−2x)(8.5−2x)=4x^{2}−39x+93.5\)
- \(h=x\)
Therefore, the volume of the box in terms of the size of the square is:
\(V=x(4x2−39x+93.5)=4x^{3}−39x^{2}+93.5x.\)
Mark can use this formula to determine the volume of the box given the length of the side of the squares he cuts out. For example, if he cuts out squares that are 2 inch by 2 inch, then x=2. The volume of the box would be:
\(V=4(2^{3})−39(2^{2})+93.5(2)=63 in^{3}\)
Example \(\PageIndex{2}\)
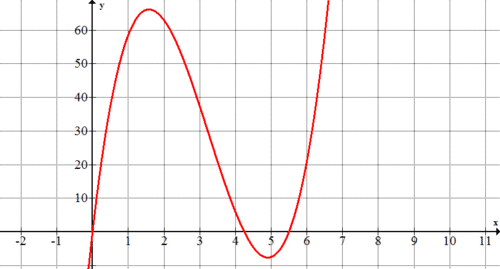
Graph the equation \(y=4x^{3}−39x^{2}+93.5x\) with a graphing calculator. What do the points on this graph represent? What portion of this graph is relevant to this problem?
Solution
The points on the graph represent the volume of the box given the length of the side of each square cut out.
Because Mark can't cut out a square with a negative side length or a square with a side length greater than 4.25 in (because the paper is only 8.5 inches wide), the portion of the graph that is relevant is the portion with \(x\) values between 0 and 4.25.
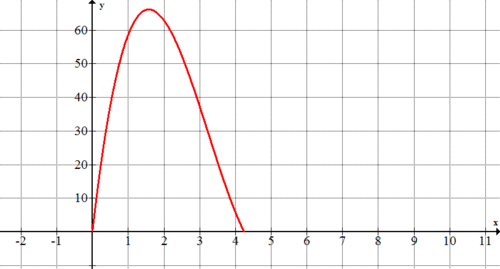
Example \(\PageIndex{3}\)
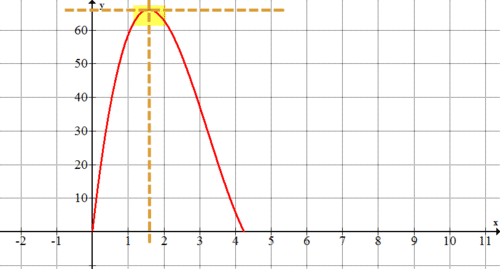
Approximately what size squares will maximize the volume of the box (cause the box to have the greatest possible volume)? How does the graph from #1 help you to answer this question?
Solution
The maximum volume looks to occur with squares that are approximately 1.6 inches by 1.6 inches. The volume at that point looks to be around \(66 in^{3}\). The graph helps to answer this question because the peak on the graph is where the maximum volume occurs.
Example \(\PageIndex{4}\)
Does the size of square that maximizes volume also maximize surface area of the box? Explain.
Solution
The surface area of the open box will be the area of the unfolded box (the net). The more you cut out of the paper, the smaller the surface area. Therefore, the size of square that maximizes volume does not also maximize surface area of the box.
Review
An 11 inch tall roll of paper towels has an inner cardboard tube with a diameter of 1.5 inches. The width of the paper towel on the roll is 2 inches and each paper towel is 0.015 inches thick.
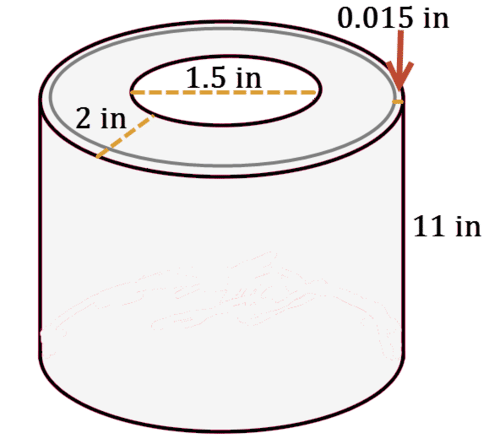
1. What is the volume of paper towels? Will the volume change if the roll of paper towels is unrolled?
2. If the whole roll of paper towels is unrolled, how long will the chain of unrolled paper towels be? [Hint: Use your answer to #1 to help]
3. Come up with an equation that generalizes the relationship between the variables: diameter of tube, width of paper towel on roll, thickness of paper towel, and length of unrolled paper towels. Why does the height of the paper towel roll not matter in this relationship?
In order to decorate a cake with purple frosting, Sam plans to fill a zipper sandwich bag with frosting, cut off one of the tips of the bag, and squeeze the frosting out of the corner (see picture below).
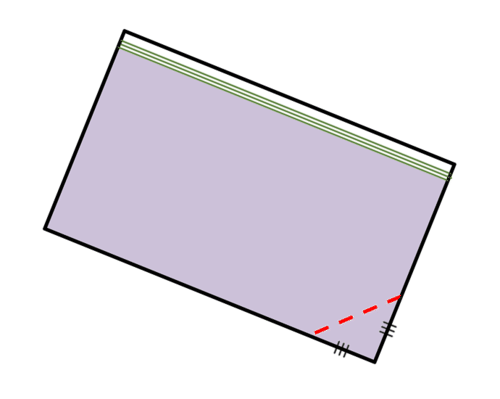
4. Assuming he cuts an isosceles triangle out of the corner, what length of cut should he make to pipe frosting with a 1 centimeter diameter. In other words, what should the length of the red dotted line be?
5. Give an equation that shows the relationship between the length of the cut made and the diameter of the frosting as it comes out of the bag.
6. You are packing up yearbooks that measure 11 inches by 14 inches by 1.5 inches. You have boxes that measure 12 inches by 30 inches by 10 inches. How many books can you fit in each box?
A certain burning candle loses \(7 in^{3} of volume each hour.

7. If the original candle was 10 inches tall with a diameter of 3 inches, what is the volume of the candle after 3 hours?
8. Create an equation that relates the original height of the candle, the diameter of the candle, the time burned, and the current volume of the candle for all candles that lose \(7 in^{3}\) of volume per hour.
9. Mike and his friends are having a water balloon fight. Each approximately spherical balloon can hold one cup of water. If one cup of water has a volume of approximately \(14.44 in^{3}\), what is the radius of each filled balloon?
Marissa works at an ice cream shop. The sugar cones have a diameter of 2 inches and a height of 4 inches. For a single scoop cone, she packs the cone with ice cream and then puts a scoop on top. For a double scoop cone, she packs the cone with ice cream and then puts two scoops on top (see sketch below). For a triple scoop cone, she packs the cone with ice cream and then puts three scoops on top. One cup of ice cream has a volume of \(14.44 in^{3}\).

10. Approximately how much ice cream (in cups) does a single scoop cone get?
11. Approximately how much ice cream (in cups) does a double scoop cone get?
12. Approximately how much ice cream (in cups) does a triple scoop cone get?
13. Describe at least two reasons why your answers to the previous three questions are only approximate.
14. If a single scoop cone costs $2.50 and a double scoop cone costs $3.50. Which type of cone is a better deal considering cost per cup of ice cream?
15. If a single scoop cone costs $2.50, what should a triple scoop cone cost if it is fairly priced?
Review (Answers)
To see the Review answers, open this PDF file and look for section 9.5.
Vocabulary
| Term | Definition |
|---|---|
| Circumference | The circumference of a circle is the measure of the distance around the outside edge of a circle. |
Additional Resources
Practice: Surface Area and Volume Applications

