9.10: Surface Area and Volume of Prisms
- Page ID
- 6205
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)3-D figures with 2 congruent bases in parallel planes and rectangles for their other faces.
Prisms
A prism is a 3-dimensional figure with 2 congruent bases, in parallel planes, in which the other faces are rectangles.
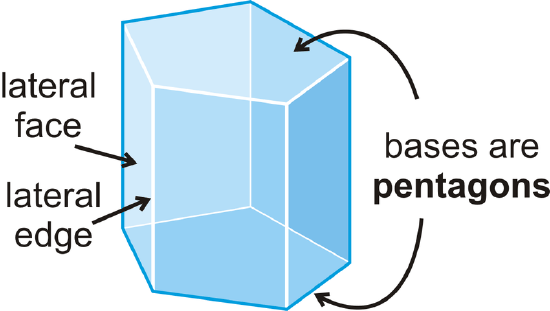
The non-base faces are lateral faces. The edges between the lateral faces are lateral edges.
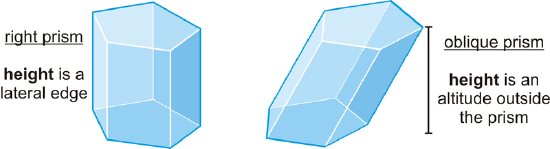
This particular example is a pentagonal prism because its base is a pentagon. Prisms are named by the shape of their base. Prisms are classified as either right prisms (prisms where all the lateral faces are perpendicular to the bases) or oblique prisms (prisms that lean to one side, whose base is a parallelogram rather than a rectangle, and whose height is perpendicular to the base's plane), as shown below.
Surface Area
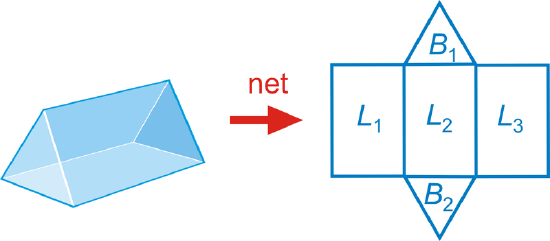
To find the surface area of a prism, find the sum of the areas of its faces. The lateral area is the sum of the areas of the lateral faces. The basic unit of area is the square unit.
\(Surface Area=B_{1}+B_{2}+L_{1}+L_{2}+L_{3}\)
\(Lateral Area=L_{1}+L_{2}+L_{3}\)
Volume
To find the volume of any solid you must figure out how much space it occupies. The basic unit of volume is the cubic unit.
For prisms in particular, to find the volume you must find the area of the base and multiply it by the height.
Volume of a Prism: \(V=B\cdot h\), where \(B= area\: of\: base\).

If an oblique prism and a right prism have the same base area and height, then they will have the same volume. This is due to Cavalieri’s Principle, which states that if two solids have the same height and the same cross-sectional area at every level, then they will have the same volume.
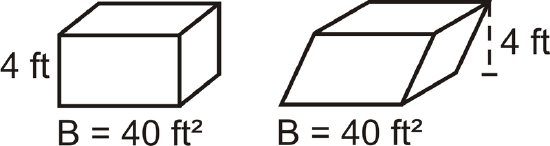
What if you were given a solid three-dimensional figure with two congruent bases in which the other faces were rectangles? How could you determine how much two-dimensional and three-dimensional space that figure occupies?
Example \(\PageIndex{1}\)
The total surface area of the triangular prism is \(540\text{ units}^{2}\). What is \(x\)?
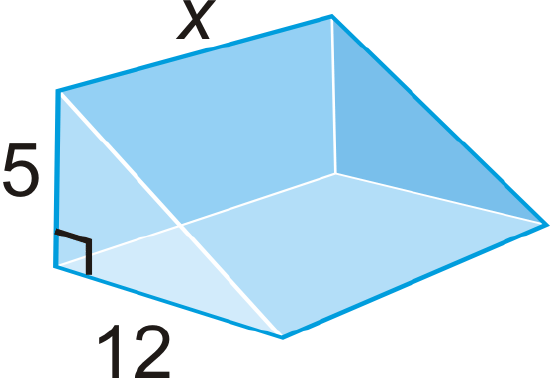
Solution
The total surface area is equal to:
\(A_{2\: triangles}+A_{3\: rectangles}=540\)
The hypotenuse of the triangle bases is 13, \(5^{2}+12^{2}\). Let’s fill in what we know.

\(\begin{aligned} A_{2\: triangles}=2(\dfrac{1}{2}\cdot 5\cdot 12)=60 \\ A_{3\: rectangles}&=5x+12x+13x=30x \\ 60+30x &=540 \\ 30x&=480 \\ x&=16\text{ units }\qquad \text{ The height is 16 units.}\end{aligned}\)
Example \(\PageIndex{2}\)
Find the volume of the right rectangular prism below.
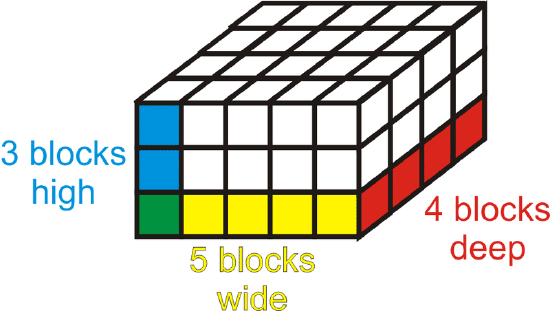
Solution
The area of the base is \((5)(4)=20\) and the height is 3. So the total volume is \((20)(3)=60\text{ unit}^{3}\)
Example \(\PageIndex{3}\)
Find the surface area of the prism below.
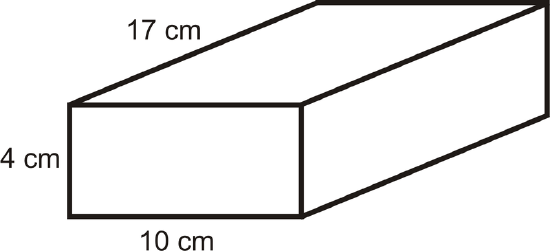
Solution
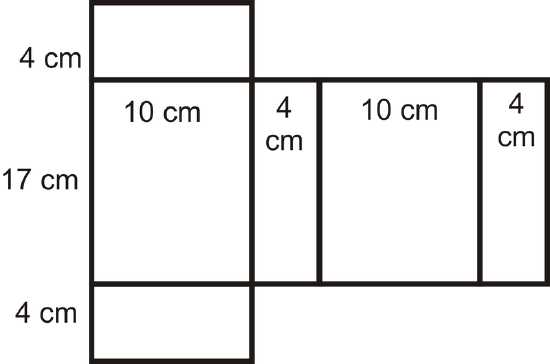
To solve, draw the net of the prism so that we can make sure we find the area of ALL faces.
Using the net, we have:
\(\begin{aligned} SA_{prism}&=2(4)(10)+2(10)(17)+2(17)(4)\\ &=80+340+136 \\ &=556 \text{ cm}^{2}\end{aligned}\)
Example \(\PageIndex{4}\)
Find the surface area of the prism below.
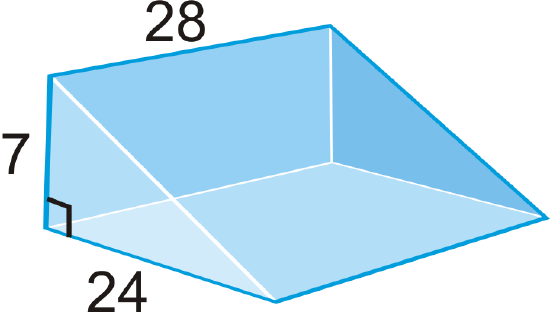
Solution
This is a right triangular prism. To find the surface area, we need to find the length of the hypotenuse of the base because it is the width of one of the lateral faces. We can use the Pythagorean Theorem to find this length.
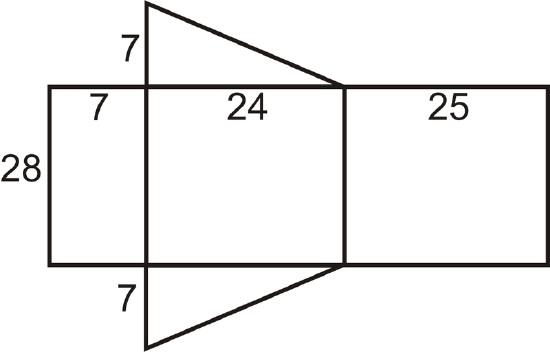
\(\begin{aligned} 7^{2}+24^{2}&=c^{2} \\ 49+576&=c^{2} \\ 625&=c^{2} \qquad c=25\end{aligned}\)
Looking at the net, the surface area is:
\(\begin{aligned} SA&=28(7)+28(24)+28(25)+2(\dfrac{1}{2}\cdot 7\cdot 24) \\ SA&=196+672+700+168=1736 units^{2}\end{aligned}\)
Example \(\PageIndex{5}\)
You have a small, triangular prism-shaped tent. How much volume does it have once it is set up?
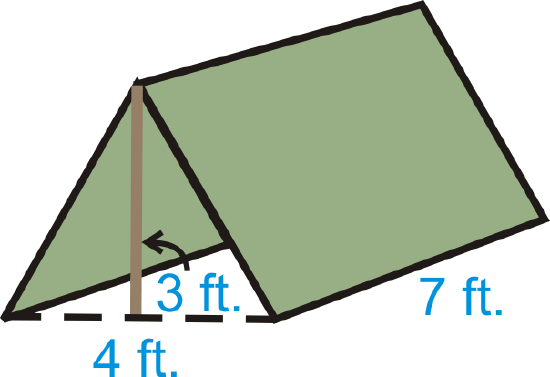
Solution
First, we need to find the area of the base.
\(\begin{aligned} B&=\dfrac{1}{2}(3)(4)=6 \text{ ft}^{2} \\ V&=Bh=6(7)=42 \text{ ft}^{3}\end{aligned}\)
Even though the height in this problem does not look like a “height,” it is because it is the perpendicular segment connecting the two bases.
Review
- What type of prism is this?
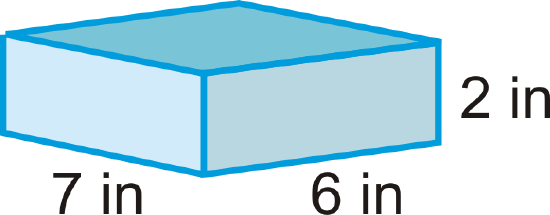
Figure \(\PageIndex{14}\) - Draw the net of this prism.
- Find the area of the bases.
- Find the area of lateral faces, or the lateral surface area.
- Find the total surface area of the prism.
- How many one-inch cubes can fit into a box that is 8 inches wide, 10 inches long, and 12 inches tall? Is this the same as the volume of the box?
- A cereal box in 2 inches wide, 10 inches long and 14 inches tall. How much cereal does the box hold?
- A can of soda is 4 inches tall and has a diameter of 2 inches. How much soda does the can hold? Round your answer to the nearest hundredth.
- A cube holds \(216\text{ in}^{3}\). What is the length of each edge?
- A cube has sides that are 8 inches. What is the volume?
Use the right triangular prism to answer questions 11-15.
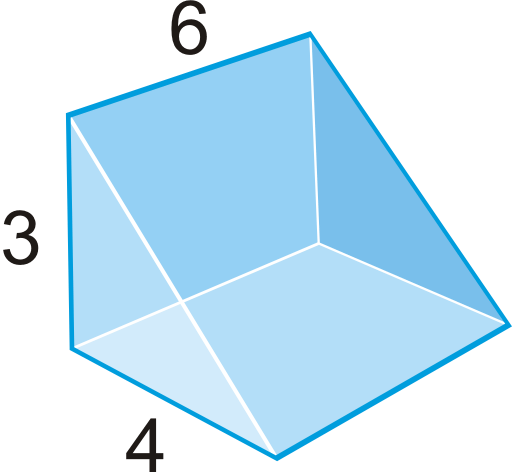
- Find the volume of the prism.
- What shape are the bases of this prism? What are their areas?
- What are the dimensions of each of the lateral faces? What are their areas?
- Find the lateral surface area of the prism.
- Find the total surface area of the prism.
- Describe the difference between lateral surface area and total surface area.
- Fuzzy dice are cubes with 4 inch sides.

Figure \(\PageIndex{16}\) - What is the volume and surface area of one die?
- What is the volume and surface area of both dice?
Find the volume of the following solids. Round your answers to the nearest hundredth.
- bases are isosceles trapezoids
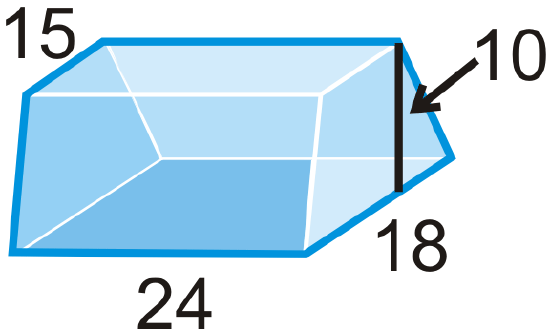
Figure \(\PageIndex{17}\) -
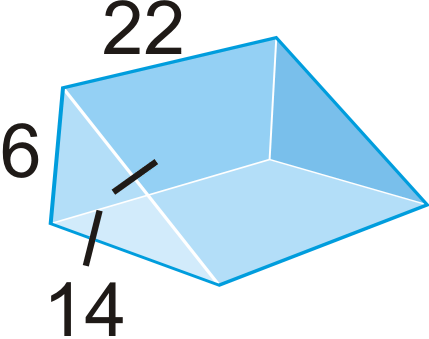
Figure \(\PageIndex{18}\) -
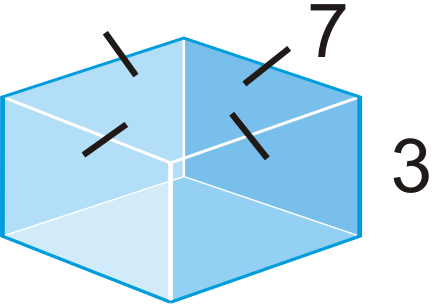
Figure \(\PageIndex{19}\) -
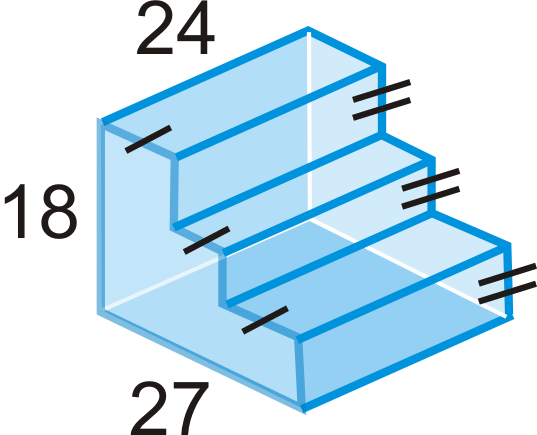
Figure \(\PageIndex{20}\)
Find the value of \(x\), given the surface area.
- \(V=504 \text{ unit}^{3} \)
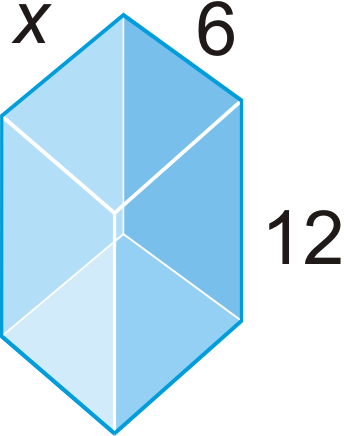
Figure \(\PageIndex{21}\) - \(V=2688\text{ unit}^{3} \)
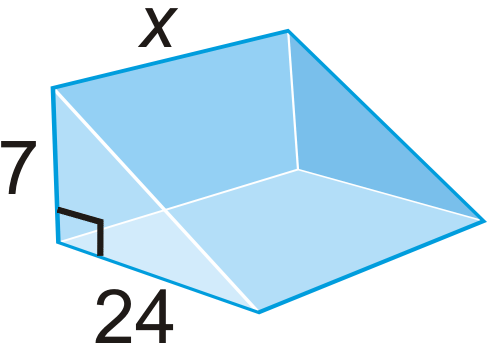
Figure \(\PageIndex{22}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 11.3.
Vocabulary
| Term | Definition |
|---|---|
| lateral edges | Edges between the lateral faces of a prism. |
| oblique prism | A prism that leans to one side and whose height is perpendicular to the base’s plane. |
| prism | is a 3-dimensional figure with 2 congruent bases, in parallel planes, and in which the other faces are rectangles. |
| right prism | A prism where all the lateral faces are perpendicular to the bases. |
| Surface Area | Surface area is the total area of all of the surfaces of a three-dimensional object. |
| Volume | Volume is the amount of space inside the bounds of a three-dimensional object. |
| Lateral Faces | All faces of a prism aside from the base are known as lateral faces. |
Additional Resources
Interactive Element
Video: Prisms Principles - Basic
Activities: Prisms Discussion Questions
Study Aids: Prisms and Cylinders Study Guide
Practice: Surface Area and Volume of Prism

