9.11: Surface Area of Prisms
- Page ID
- 6211
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Use formulas to find the surface area of a rectangular prisms and triangular prisms.
Surface Area of Triangular Prisms

Max bought a light prism for his mom for Mother's Day. He wants to figure out how much wrapping paper is needed to wrap it. To do this, he needs to figure out the surface area of the gift. The triangular end has a base of 3 cm and height of 4 cm. The length of each side is 6 cm and the height of the prism (length of the rectangular side) is 8 cm. What is the surface area of the gift that Max bought for his mom?
In this concept, you will learn how to calculate the surface area of a triangular prism.
Finding the Surface Area of a Triangular Prism
Area is the space that is contained in a two-dimensional figure. Surface area is the total area of all of the sides and faces of a three-dimensional figure. To find the surface area, the area of each face is calculated and then add these areas together.
One way to do this is to use a net, since a net is a two-dimensional representation of a three-dimensional solid, or an unfolded picture of a solid.
What is the surface area of the figure below?
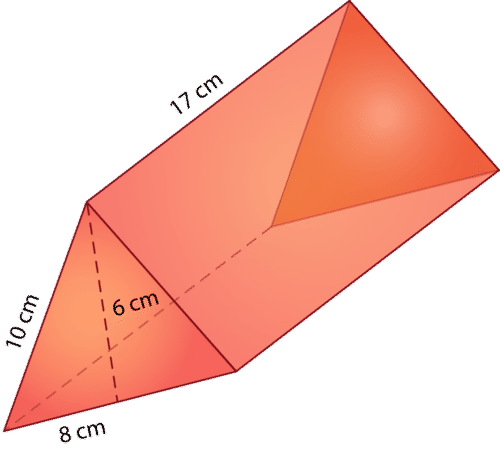
The net for this triangular prism is as follows:
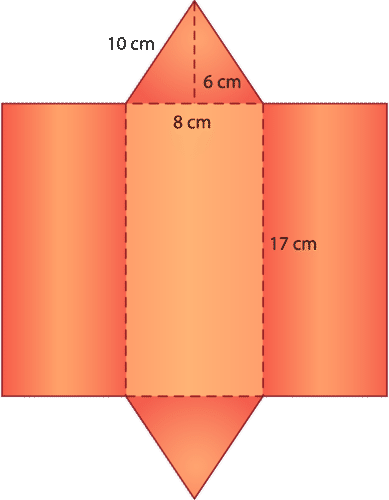
Now, let's fill in the measurements for the sides of each face in order to calculate their area. Triangular prisms have their own formula for finding surface area because they have two triangular faces opposite each other.
The formula \( A=\dfrac{1}{2}bh\) is used to find the area of the top and bases triangular faces, where A = area, b = base, and h = height. The formula \(A=lw\) is used to find the area of the three rectangular side faces, where A = area, l = length, and w = width.
Plugging in the measurements that are given in the net, calculate the area of each face. Remember to use the correct area formula for the triangles and rectangles.
\(\begin{array}{llllll}
\text { Bottom face } & \text { Top face } & \text { side } & \text { side } & \text { side } \\
A=\frac{1}{2} b h & A=\frac{1}{2} b h & A=l w & A=l w & A=l w \\
\frac{1}{2}(8)(6)+ & \frac{1}{2}(8)(6)+ & 17 \times 10+ & 17 \times 10+ & 17 \times 8 \\
24 & + & 24 & + & 170 & + & 170 & + & 136 \\
=524 \mathrm{~cm}^{2} & & & &
\end{array}\)
When you add these values together, you get a surface area of 524 square centimeters for this triangular prism.
\(SA=bh+(s_{1}+s_{2}+s_{3})H\)
You can also use one formula to calculate the surface area of a triangular prism which can save time over the process of using a net to derive the areas:
where b = base; h = height of the triangle; s_{1}\), s_{2}\), and s_{3}\) = the length of each side of the triangle base, and H = the height of the prism (which is the length of the rectangles).
First, find the area of the two triangular faces. Each face will have an area of 12bh. Remember, you can use a formula to calculate the area of a pair of faces. Therefore, you can double this formula to find the area of both triangular faces at once which results in the formula 2(12bh). The 2 multiplied by the 12 equals 1, or cancels each other out, and you're left with bh.
Next, you need to calculate the area of each of the rectangular side faces. The length of each rectangle is the same as the height of the prism, so call this H. The width of each rectangle is actually the same as the sides of the triangular base. Instead of multiplying the length and width for each rectangle, you can combine this information. Since there are 3 rectangular widths (all equal to the sides of the triangles), multiply the perimeter of the triangular base by the height of the rectangles, H, which will give the area of all three rectangles.
If you put these pieces together—the area of the bases and the area of the side faces—you get this formula:
\(SA=bh+(s_{1}+s_{2}+s_{3})H\)
where bh = the area of the triangle top and base, and (\(s_{1}+s_{2}+s_{3})H\) = the area of the rectangular side faces.
Remember that the height of the triangular base (\(h\)) is not necessarily the same as the height of the prism (H).
Example \(\PageIndex{1}\)
Earlier, you were given a problem about the gift Max bought for his mom.
The triangular end has a base of 3 cm and height of 4 cm. The length of each side is 6 cm and the height of the prism (length of the rectangle) is 8 cm. What is the surface area of this triangular prism?
Solution
First, substitute the given values into the formula.
\(\begin{aligned} SA&=bh+(s_{1}+s_{2}+s_{3})H \\ SA&=3(4)+(3+6+6)(8)\end{aligned}\)
Next, multiply the base times height for the area of the triangles (bh), and add their three sides (\(s_{1} + s_{2} + s_{3}\)).
\(SA=12+15(8)\)
Then, multiply the sum of the triangle sides by the height of the prism (H\)) and add the values together for the answer, remembering to include the appropriate unit of measurement.
\(\begin{aligned} SA&=12+120 \\ SA&=132\text{ cm}^{2}\end{aligned}\)
The answer is the surface area of the gift Max bought for his mom is 132 square centimeters.
Example \(\PageIndex{1}\)
Calculate the surface area of the following triangular prism:
Solution
First, substitute the given values into the formula.
\(\begin{aligned} SA&=bh+(s_{1}+s_{2}+s_{3})H \\ SA&=4(6)+(4+7+7)(12)\end{aligned}\)
Next, multiply the base times height for the area of the triangles (bh) and add the three sides of the triangle (\(s_{1} + s_{2} + s_{3}\)).
\(SA=24+18(12)\)
Then, multiply the sum of the triangle sides by the height of the prism (H) and add the values together for the answer, making sure to include the appropriate unit of measurement.
\(\begin{aligned} SA&=24+216 \\ SA&=240 cm^{2}\end{aligned}\)
The answer is the surface area of the above triangular prism is 240 square centimeters.
Example \(\PageIndex{1}\)
A triangular prism has a triangular end with a base of 5 inches and a height of 4 inches. The length of each side is 8 inches and the width of each side is 6 inches. What is the surface area of the prism?
Solution
First, substitute the given values into the formula.
\(\begin{aligned} SA&=bh+(s_{1}+s_{2}+s_{3})H \\ SA&=5(4)+(5+6+6)(8)\end{aligned}\)
Next, multiply the base times height for the area of the triangles (bh), and add their three sides (s_{1} + s_{2} + s_{3}\)).
\(SA=20+17(8)\)
Then, multiply the sum of the triangle sides by the height of the prism (H) and add the values together for the answer, remembering to include the appropriate unit of measurement.
\(\begin{aligned} SA&=20+136 \\ SA&=156\text{ in}^{2}\end{aligned}\)
The answer is the surface area of the above triangular prism is 156 square inches.
Example \(\PageIndex{1}\)
A triangular prism has a triangular end with a base of 8 feet and a height of 6 feet. The length of each side is 10 feet and the width of each side is 6 feet. What is the surface area of the prism?
Solution
First, substitute the given values into the formula.
\(\begin{aligned} SA&=bh+(s_{1}+s_{2}+s_{3})H \\ SA&=8(6)+(8+6+6)(10)\end{aligned}\)
Next, multiple the base times height for the area of the triangles (bh), and add the three sides of the triangle (s_{1} + s_{2} + s_{3}\)).
\(SA=48+20(10)\)
Then, multiply the sum of the triangle sides by the height of the prism (H) and add the values together for the answer, making sure to include the appropriate unit of measurement.
\(\begin{aligned} SA&=48+200 \\ SA&=248\text{ ft}^{2}\end{aligned}\)
The answer is the surface area of the above triangular prism is 248 square feet.
Example \(\PageIndex{1}\)
A triangular prism has a triangular end with a base of 12 inches and a height of 9 inches. The length of each side is 14 inches and the width of each side is 9 inches. What is the surface area of the prism?
Solution
First, substitute the given values into the formula.
\(\begin{aligned} SA&=bh+(s_{1}+s_{2}+s_{3})H \\ SA&=12(9)+(9+9+9)(14)\end{aligned}\)
Next, multiply the base times height for the area of the triangles (bh\)), and add the three sides of the triangle (\(s_{1} + s_{2} + s_{3}\)).
\(SA=108+27(14)\)
Then, multiply the sum of the triangle sides by the height of the prism (H\)) and add the values together for the answer, making sure to include the appropriate unit of measurement.
\(\begin{aligned} SA&=108+378 \\ SA&=486\text{ in}^{2}\end{aligned}\)
The answer is the surface area of the above triangular prism is 486 square inches.
Review
Use the following figure to answer each question.
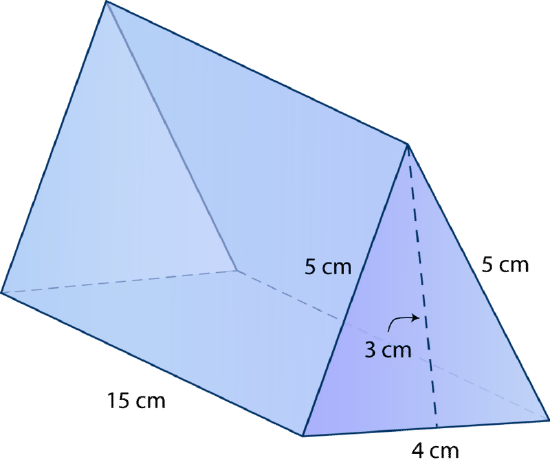
- What unit are the measurements of this figure?
- What is the length of the base?
- What is the width of the base?
- What is the shape of the sides?
- What is the measure of the triangular side?
- What is the formula for finding the surface area of a triangular prism?
- What is the surface area of this figure?
Find the surface area of each triangular prism.
- A triangular prism has a triangular end with a base of 4 inches and a height of 3 inches. The length of each side is 5 inches and the width of each side is 3 inches. What is the surface area of the prism?
- A triangular prism has a triangular end with a base of 4 feet and a height of 5 feet. The length of each side is 6 feet and the width of each side is 5 feet. What is the surface area of the prism?
- A triangular prism has a triangular end with a base of 3 inches and a height of 3 inches. The length of each side is 4 inches and the width of each side is 3 inches. What is the surface area of the prism?
- A triangular prism has a triangular end with a base of 6 meters and a height of 5 meters. The length of each side is 8 meters and the width of each side is 5 meters. What is the surface area of the prism?
- A triangular prism has a triangular end with a base of 15 feet and a height of 10 feet. The length of each side is 12 feet and the width of each side is 10 feet. What is the surface area of the prism?
- A triangular prism has a triangular end with a base of 9 inches and a height of 7 inches. The length of each side is 9 inches and the width of each side is 7 inches. What is the surface area of the prism?
- A triangular prism has a triangular end with a base of 8 inches and a height of 6 inches. The length of each side is 15 inches and the width of each side is 6 inches. What is the surface area of the prism?
- A triangular prism has a triangular end with a base of 5.5 feet and a height of 4 feet. The length of each side is 9 feet and the width of each side is 5 feet. What is the surface area of the prism?
Review (Answers)
To see the Review answers, open this PDF file and look for section 10.5.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Area | Area is the space within the perimeter of a two-dimensional figure. |
| Prism | A prism is a three-dimensional object with two congruent parallel bases that are polygons. |
| Surface Area | Surface area is the total area of all of the surfaces of a three-dimensional object. |
| Triangular Prism | A triangular prism is a prism made up of two triangular bases and three rectangular faces. |
Additional Resources
Interactive Element
Video: Find the Surface Area of an Open Top Box
Practice: Surface Area of Prisms

