9.12: Volume of Prisms
- Page ID
- 6221
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Use the formula \(V = Bh\)

Karen and Lance are building a backyard playground for their two children. They have a swing set, a merry-go-round, and a sandbox already set up. Lance is going to the store to buy sand for the sandbox and needs to know how much sand it can hold. The sandbox is 6 feet wide, 8 feet long, and 1 feet deep. How can Lance use a formula to calculate the total volume of this sandbox?
In this concept, you will learn to find volumes of rectangular and triangular prisms using formulas.
Finding Volume of Prisms
Volume is the amount of space inside a solid figure.
Filling solid figures with cubes is a simple, easy way to understand volume. If you can count the cubes, you can figure out the volume. However, sometimes you will have to figure out the volume of a prism when there aren’t any cubes drawn inside it.
Take a look at the prism below.
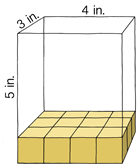
This rectangular prism has a height of 5 inches, a width of 3 inches, and a length of 4 inches.
Here is a formula for finding the volume of this type prism.
\(V=Bh\)
B means the area of the base, which is the length times the width, and h means the height.
So, first figure out the area of the base.
\(A=3\times 4=12\)
Next, multiply \(B\) by \(h\).
\(\begin{aligned} h&=5\\ V&=12\times 5=60\end{aligned}\)
The volume is 60 cubic inches or \(in^{3}\). Remember, volume is in cubic units.
Let’s look at another example. Find the volume using the volume formula.
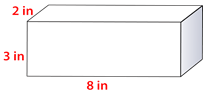
\(V=Bh\)
First, figure the area of the base.
The area of the base is \(2\times 8=16\)
Next, multiply the B by h. The height is 3 inches.
\(\begin{aligned} V&=16\times 3 \\ V&=48\: \text{ in}^{3}\end{aligned}\)
The volume of this rectangular prism is \(48\:\text{ in}^{3}\).
You can use the same formula for finding the volume of the triangular prism. Except this time, the area of the base is a triangle and not a rectangle.
Take a look at the triangular prism below.
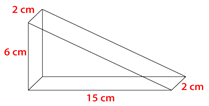
To find the volume of a triangular prism, multiply the area of the base (\(B\)) with the height of the prism.
\(V=Bh\)
First, find the area of the triangular base using the formula for area of a triangle.
\(\begin{aligned} A&=\dfrac{1}{2}bh \\ A&=\dfrac{1}{2}(15\times 6) \\ A&=\dfrac{1}{2}(90) \\ A&=45\:\text{ sq. units}\end{aligned}\)
Next, multiply this by the height.
\(\begin{aligned} V&=Bh \\ V&=(45)h \\ V&=45(2) \\ V&=90\text{ cubic centimeters} or \text{ cm}^{3}\end{aligned}\)
The volume of the prism is \(90\text{ cm}^{3}\).
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Lance and Karen’s sandbox.
The sandbox is 6 feet wide, 8 feet long, and 1 feet deep. Lance needs to know the volume.
Solution
To find the volume of the sandbox, which is a prism with one of its bases removed, use the following formula.
\(V=Bh\)
First, substitute in the given values. Remember, B is length times width.
\(\begin{aligned} V&=(8\times 6)(1)\\ V&=48\text{ ft}^{3}\end{aligned}\)
This is the total volume.
Next, to find out how much sand he needs to fill the sandbox halfway, divide the total volume by 2.
\(48\divide 2=24\)
Lance needs 24 cubic feet of sand to fill the sandbox halfway.
Example \(\PageIndex{2}\)
Find the volume of the prism.
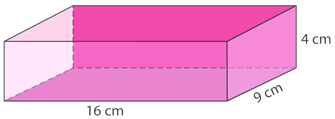
Solution
To find the volume of a prism, use the following formula.
\(V=Bh\)
First, substitute in the given values. Remember B is length times width.
\(\begin{aligned} V&=(16\times 9)(4) \\ V&=576\text{ cm}^{3}\end{aligned}\)
The answer is \(576\text{ cm}^{3}\).
Example \(\PageIndex{3}\)
Find the volume of the prism.
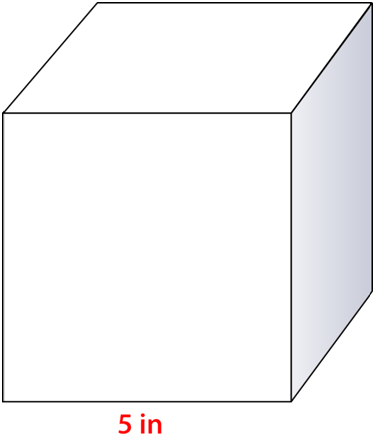
Solution
First, to find the volume of a prism, use the following formula.
\(V=Bh\)
Next, substitute in the given values. Remember B is length times width. This is a square cube, so the length, width, and height are the same.
\(\begin{aligned} V&=(5\times 5)(5) \\V&=125\text{ in}^{3}\end{aligned}\)
The answer is \(125\text{ in}^{3}\).
Example \(\PageIndex{4}\)
Find the volume of the prism.
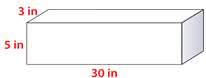
Solution
First, to find the volume of a prism, use the following formula.
\(V=Bh\)
First, substitute in the given values. Remember, B is length times width.
\(\begin{aligned} V&=(30\times 5)(3) \\ V&=450\text{ in}^{3}\end{aligned}\)
The answer is \(450\text{ in}^{3}\).
Example \(\PageIndex{5}\)
Find the volume of the prism.
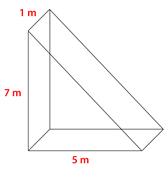
Solution
To find the volume of a triangular prism, multiply the area of the base (B) with the height of the prism.
\(V=Bh\)
First, find the area of the triangular base using the formula for area of a triangle.
\(\begin{aligned} A&=\dfrac{1}{2}bh \\ A&=\dfrac{1}{2}(5\times 7) \\ A&=\dfrac{1}{2}(35) \\ A&=17.5 \text{ sq. m} \end{aligned}\)
Next, multiply this by the height.
\(\begin{aligned} V&=Bh \\ V&=(17.5)1 \\ V&=17.5\text{ cm}^{3}\end{aligned}\)
The volume of the prism is \(17.5\text{ cm}^{3}\).
Review
Find the volume of each rectangular prism. Remember to label your answer in cubic units.
- Length = 5 in, width = 3 in, height = 4 in
- Length = 7 m, width = 6 m, height = 5 m
- Length = 8 cm, width = 4 cm, height = 9 cm
- Length = 8 cm, width = 4 cm, height = 12 cm
- Length = 10 ft, width = 5 ft, height = 6 ft
- Length = 9 m, width = 8 m, height = 11 m
- Length = 5.5 in, width = 3 in, height = 5 in
- Length = 6.6 cm, width = 5 cm, height = 7 cm
- Length = 7 ft, width = 4 ft, height = 6 ft
- Length = 15 m, width = 8 m, height = 10 m
Find the volume of each triangular prism. Remember that h\) means the height of the triangular base and H\) means the height of the whole prism.
- \(b=6\text{ in}\), \(h=4\text{ in}\), \(H=5\text{ in}\)
- \(b=7\text{ in}\), \(h=5\text{ in}\), \(H=9\text{ in}\)
- \(b=10\text{ m}\), \(h=8\text{ m}\), \(H=9\text{ m}\)
- \(b=12\text{ m}\), \(h=10\text{ m}\), \(H=13\text{ m}\)
- \(b=8\text{ cm}\), \(h=6\text{ cm}\), \(H=9\text{ cm}\)
Answer true or false for each of the following questions.
- Volume is the amount of space that a figure can hold inside it.
- The volume of a rectangular prism is always greater than the volume of a cube.
- The volume of a triangular prism is less than a rectangular prism with the same size base.
- A painter would need to know the surface area of a house to do his/her job correctly.
- If Marcus is covering his book with a book cover, Marcus is covering the surface area of the book.
Vocabulary
| Term | Definition |
|---|---|
| Net | A net is a diagram that shows a “flattened” view of a solid. In a net, each face and base is shown with all of its dimensions. A net can also serve as a pattern to build a three-dimensional solid. |
| Rectangular Prism | A rectangular prism is a prism made up of two rectangular bases and four rectangular faces. |
| Surface Area | Surface area is the total area of all of the surfaces of a three-dimensional object. |
| Triangular Prism | A triangular prism is a prism made up of two triangular bases and three rectangular faces. |
Additional Resources
Interactive Element
Video: Solid Geometry Volume
Practice: Volume of Prisms

