9.13: Volume of Prisms Using Unit Cubes
- Page ID
- 6222
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Use cubes to find the volume of a prism.

Jerry’s assignment in his carpentry class is to build a wooden storage container that will hold at least 48 cubic units of material. Jerry has already started on the rectangular container, which is 4 units wide and 2 units long. Jerry isn’t sure what height the container should be in order to hold a volume of 48 cubic units. How can Jerry use this information to determine the height of the container?
In this concept, you will learn to identify the volume of prisms using unit cubes.
Finding Volume of Prisms Using Unit Cubes
Volume is the amount of space inside a solid figure.
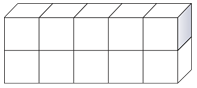
These cubes make up a rectangular prism. The cubes represent the volume of the prism. This prism is five cubes by two cubes by one cube. In other words, it is five cubes long, by two cubes high by one cube wide. You can multiply each of these values together to get the volume of the rectangular prism.
\(5\times 2\times 1=10\text{ cubic units }\)
The volume of the rectangular prism is 10 cubic units or \(\text{ units}^{3}\). The units are cubic units because you multiplied the units 3 times when you multiplied the height, length, and width.
Here is another prism.
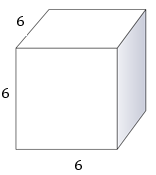
First, to figure out the volume of this prism, identify the measurements.
Length - 6
Width - 6
Height - 6
Next, substitute these values in the formula for volume then solve.
\(\text{Length }\times \text{ Width }\times \text{ Height}=\text{ Volume in cubic units}\)
\(6\times 6\times 6=216\text{ cubic units}\)
The volume of the cube is \(216\text{ cubic units}\).
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Jerry and the storage container he is building.
The container is 4 units wide and 2 units long when he learned about the volume requirement. The container needs to have a volume of 48 cubic units. How can Jerry use this information to determine the height the container should be?
Solution
First, to figure the height the container should be, identify the given measurements.
Length - 2 units
Width - 4 units
Height - ?
Volume - 48 cubic units
Next, substitute these values into the formula for volume.
\(\begin{aligned} \text{ Length }\times \text{ Width} \times \text{ Height}&=Volume in cubic units \\ 2\times 4\times H&=48 \text{ cubic units}\end{aligned}\)
Then, multiply.
\(8(H)=48\)
Then, divide both sides by 8.
\(H=6\text{ units}\)
The container should have a height of 6 units.
Example \(\PageIndex{2}\)
What is the volume of this figure?

Solution
First, to figure out the volume of this prism, identify the measurements.
Length - 4 units
Width - 4 units
Height - 3 units
Next, substitute these values into the formula for volume then solve.
\(\begin{aligned} \text{ Length}\times \text{ Width}\times \text{ Height}=\text{ Volume in cubic units} \\ 4\times 4\times 3=216 \text{ cubic units}\end{aligned}\)
The volume of the prism is \(48\text{ cubic units}\), or \(48 \text{ units}^{3}\).
Example \(\PageIndex{3}\)
Find the volume of the prism.
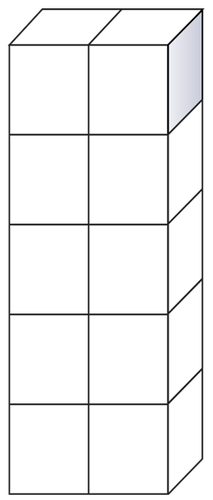
Solution
First, to figure out the volume of this prism, identify the measurements.
Length - 1
Width - 2
Height - 5
Next, substitute these values into the formula for volume then solve.
\(\begin{aligned} \text{Length}\times \text{ Width}\times \text{Height}&=\text{Volume in cubic units} \\ 1\times 2\times 5&=10 \text{ cubic units}\end{aligned}\)
The volume of the prism is 10 cubic units.
Example \(\PageIndex{4}\)
Find the volume of the prism.
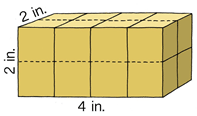
Solution
First, to figure out the volume of this prism, identify the measurements.
Length - 2 inches
Width - 4 inches
Height - 2 inches
Next, substitute these values into the formula for volume then solve.
\(\begin{aligned} \text{Length}\times \text{Width}\times \text{Height}&=\text{ Volume in cubic units}\\ 2\times 4\times 2&=16 \text{ cubic inches}\end{aligned}\)
The volume of the cube is 16 cubic inches.
Example \(\PageIndex{5}\)
Find the volume of the prism.
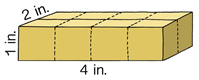
Solution
First, to figure out the volume of this prism, identify the measurements.
Length - 2 inches
Width - 4 inches
Height - 1 inch
Next, substitute these values into the formula for volume then solve.
\(\begin{aligned} \text{Length}\times \text{Width}\times \text{Height}&=\text{ Volume in cubic units}\\ 2\times 4\times 1&=8 \text{ cubic units}\end{aligned}\)
The volume of the prism is 8 cubic inches.
Review
Find the volume of each prism.
-
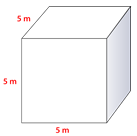
Figure \(\PageIndex{8}\) -
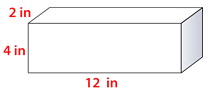
Figure \(\PageIndex{9}\) -
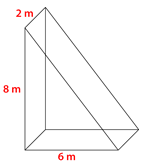
Figure \(\PageIndex{10}\) -
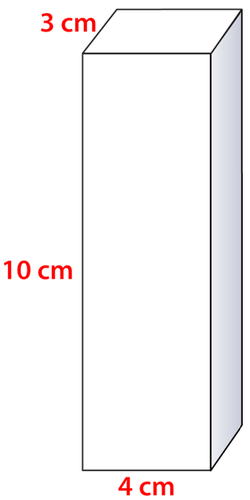
Figure \(\PageIndex{11}\) -
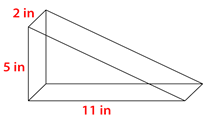
Figure \(\PageIndex{12}\) -
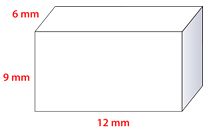
Figure \(\PageIndex{13}\) -
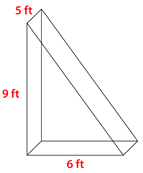
Figure \(\PageIndex{14}\) -
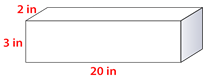
Figure \(\PageIndex{15}\) -
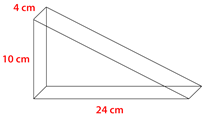
Figure \(\PageIndex{16}\) -
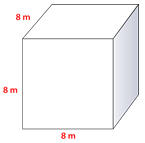
Figure \(\PageIndex{17}\)
Identify each type of prism.
-

Figure \(\PageIndex{18}\) -

Figure \(\PageIndex{19}\) -

Figure \(\PageIndex{20}\) -

Figure \(\PageIndex{21}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 10.15.
Vocabulary
| Term | Definition |
|---|---|
| Net | A net is a diagram that shows a “flattened” view of a solid. In a net, each face and base is shown with all of its dimensions. A net can also serve as a pattern to build a three-dimensional solid. |
| Rectangular Prism | A rectangular prism is a prism made up of two rectangular bases and four rectangular faces. |
| Surface Area | Surface area is the total area of all of the surfaces of a three-dimensional object. |
| Triangular Prism | A triangular prism is a prism made up of two triangular bases and three rectangular faces. |
| Volume | Volume is the amount of space inside the bounds of a three-dimensional object. |
Additional Resources
Video: Solid Geometry Volume
Practice: Volume of Prisms Using Unit Cubes

