9.14: Volume of Rectangular Prisms
- Page ID
- 6223
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Volume equals length times width times height

Ben's mom has grown frustrated with Ben's extensive Lego collection thrown all over his bedroom floor. She gives him a choice of three different boxes in which to store them. Ben wants to choose the box that will hold the most Legos. While the boxes are different in dimensions, Ben cannot figure out which will hold the most. The box measurements are as follows:
Box A: height = 5 inches, length = 18 inches, width = 10
Box B: height = 8 inches, length = 10 inches, width = 12 inches
Box C: height = 6 inches, length = 14 inches, width = 10 inches.
Which box has the greatest volume?
In this concept, you will learn how to figure out the volume of rectanglar prisms.
Finding the Volume of a Rectangular Prism
Volume is the measure of how much three-dimensional space an object takes up or holds.
Imagine a fish aquarium. Its length, width, and height determine how much water the tank will hold. If you fill it with water, the amount of water is the volume that the tank will hold. You measure volume in cubic units, because you are multiplying three dimensions: length, width, and height.
One way to find the volume of a prism is to consider how many unit cubes it can contain. A unit cube is simply a cube measuring one inch, one centimeter, one foot, or whatever unit of measurement you are using, on all sides. Here are some unit cubes.
To use unit cubes to calculate volume, simply count the number of unit cubes that fit into the prism. Begin by counting the number of cubes that cover the bottom of the prism, and then count each layer. Let’s see how this works.
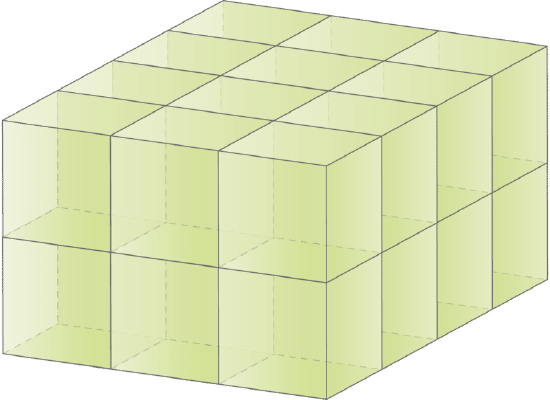
How many cubes do you see here? If you count all of the cubes, you will see that there are 24 cubes in this prism.
The volume of this prism is \(24 \text{ units}^{3}\) or cubic units.
Find the volume of the following figure using unit cubes.
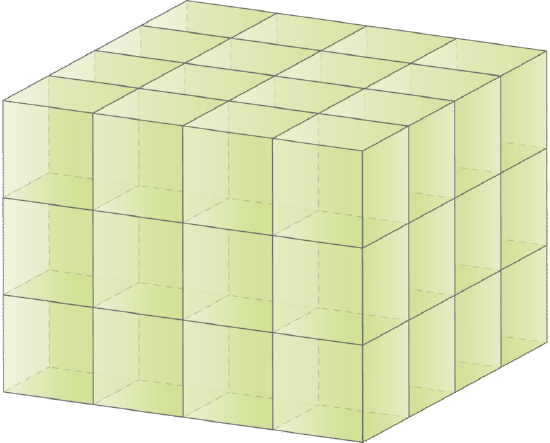
How many cubes are in this figure? If you count the cubes, you will get a total of 48 cubes. The volume of this prism is 48 cubic units or \(\text{ units}^{3}\).
If you look carefully, you will see that the volume of the rectangular prism is a function of multiplying the length \times the width \times the height. You just discovered the formula for finding the volume of a rectangular prism. Now let’s refine that formula a little further. Here is the formula.
\(V=Bh\)
The volume is equal to the B, base area of the prism, times the height of the prism.
Let's look at an example.
Find the volume of the prism below.

Simply put the values for the length, width, and height in for the appropriate variables in the formula, then solve for V, volume.
First find the area of the base. This is the rectangular side on the bottom. Remember, to find the area of a rectangle, multiply the length times the width.
\(\begin{aligned} B&=lw \\ B&=16\times 9 \\ B&=144\text{ cm}^{2}\end{aligned}\)
The base area is 144 square centimeters. Now multiply this by the height.
\(\begin{aligned}V&=Bh \\ V&=144\times 4 \\ V&=576 \text{ cm}^{3}\end{aligned} \)
You can use the following formula for volume of a rectangular prism. This combines the two steps that you completed above:
\(\begin{aligned} V&=lwh \\ V&=(16)(9)(4) \\V&=576\text{ cm}^{3}\end{aligned}\)
The volume of this rectangular prism is 576 cubic centimeters.
You can work with the same rectangular prism, but fill it with unit cubes.

You can count the unit cubes here to find the volume of the rectangular prism. However, you save time by using the formula for volume.
Let's look at another example.
Find the volume of a container with a length of 15 ft, width of 12 ft, and height of 11 ft.
First, plug the values of the dimensions into the formula for volume of a rectangular prism and multiply the values for length and width:
\(\begin{aligned} V&=lwh \\ V&=(15)(12)(11) \\ V&=(180)(11)\end{aligned}\)
Next, multiply the results by the value for the height:
\(\begin{aligned} V&=(180)(11) \\V&=1,980\end{aligned}\)
Then, record the answer including the appropriate unit of measurement:
\(V=1,980\text{ ft}^{3}\)
The answer is the container has a volume of 1,980 cubic feet.
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Ben, who is searching for the box that will hold the most Legos.
Ben needs to figure out which of the following boxes has the greatest volume.
Box A: height = 5 inches, length = 18 inches, width = 10 inches
Box B: height = 8 inches, length = 10 inches, width = 12 inches
Box C: height = 6 inches, length = 14 inches, width = 10 inches
Solution
First, plug the values of the dimensions into the formula for volume of a rectangular prism and multiply the values for length and width:
Box A: \(V=(5)(18)(10)\)
\(V=(90)(10) \)
Box B: \(V=(8)(10)(12)\)
\(V=(80)(12) \)
Box C: \(V=(6)(14)(10)\)
\(V=(84)(10)\)
Next, multiply the results by the value for the height:
Box A: \(V=(90)(10)\)
\(V=900\)
Box B: \(V=(80)(12)\)
\(V=960\)
Box C: \(V=(84)(10)\)
\(V=840\)
Then, record the answer including the appropriate unit of measurement:
Box A: \(V=900\text{ in}^{2}\)
Box B: \(V=960\text{ in}^{2} \)
Box C: \(V=840\text{ in}^{2}\)
The answer is Box B has the greatest volume and therefore can hold the most Legos.
Example \(\PageIndex{2}\)
Carla is cleaning out her fish tank, so she filled the bathtub to the rim with water for her fish to swim in while she empties their tank. If the bathtub is 5.5 feet long, 3.3 feet wide, and 2.2 feet deep, how much water can it hold?
Solution
First, plug the values of the dimensions into the formula for volume of a rectangular prism and multiply the values for length and width:
\(\begin{aligned} V&=lwh \\ V&=(5.5)(3.3)(2.2) \\ V&=(18.15)(2.2)\end{aligned}\)
Next, multiply the results by the value for the height:
\(\begin{aligned} V&=(18.15)(2.2) \\ V&=39.93\end{aligned}\)
Then, record the answer including the appropriate unit of measurement:
\(V=39.93\text{ ft}^{3}\)
The answer is Carla’s bathtub can hold 39.93 cubic feet of water.
Example \(\PageIndex{3}\)
Find the volume of a container with a length of 10 inches, width of 8 inches, and height of 6 inches.
Solution
First, plug the values of the dimensions into the formula for volume of a rectangular prism and multiply the values for length and width:
\(\begin{aligned} V&=lwh \\ V&=(10)(8)(6) \\ V&=(80)(6)\end{aligned}\)
Next, multiply the results by the value for the height:
\(\begin{aligned} V&=(80)(6) \\ V&=480\end{aligned}\)
Then, record the answer including the appropriate unit of measurement:
\(V=480\text{ in}^{3}\)
The answer is the container has a volume of 480 cubic inches.
Example \(\PageIndex{4}\)
Find the volume of a container with a length of 8 meters, width of 7 meters, and height of 3 meters.
Solution
First, plug the values of the dimensions into the formula for volume of a rectangular prism and multiply the values for length and width:
\(\begin{aligned} V&=lwh \\ V&=(8)(7)(3) \\ V&=(56)(3)\end{aligned}\)
Next, multiply the results by the value for the height:
\(\begin{aligned} V&=(56)(3) \\ V&=168\end{aligned}\)
Then, record the answer including the appropriate unit of measurement:
\(V=168\text{ m}^{3}\)
The answer is the container has a volume of 168 cubic meters.
Review
Find the volume of each rectangular prism. Remember to label your answer in cubic units.
- Length = 5 in, width = 3 in, height = 4 in
- Length = 7 m, width = 6 m, height = 5 m
- Length = 8 cm, width = 4 cm, height = 9 cm
- Length = 8 cm, width = 4 cm, height = 12 cm
- Length = 10 ft, width = 5 ft, height = 6 ft
- Length = 9 m, width = 8 m, height = 11 m
- Length = 5.5 in, width = 3 in, height = 5 in
- Length = 6.6 cm, width = 5 cm, height = 7 cm
- Length = 7 ft, width = 4 ft, height = 6 ft
- Length = 15 m, width = 8 m, height = 10 m
- Length = 10.5 m, width = 11 m, height = 4 m
- Length = 12 ft, width = 12 ft, height = 8 ft
- Length = 16 in, width = 8 in, height = 8 in
- Length = 12 m, width = 12 m, height = 12 m
- Length = 24 in, width = 6 in, height = 6 in
Review (Answers)
To see the Review answers, open this PDF file and look for section 10.10.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Cubic Units | Cubic units are three-dimensional units of measure, as in the volume of a solid figure. |
| Prism | A prism is a three-dimensional object with two congruent parallel bases that are polygons. |
| Volume | Volume is the amount of space inside the bounds of a three-dimensional object. |
Video: Solid Geometry Volume
Practice: Volume of Rectangular Prisms

