9.15: Volume of Triangular Prisms
- Page ID
- 6224
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Volume equals base times height times half of length.

Maggie is enjoying her favorite chocolate. She wonders how much chocolate can fit into the packaging, which is in the shape of a triangular prism. She measures the cardboard prism and finds that the triangle end, or base, is 1.4 inches, and the height of the triangle is 1.25 inches. The height of the bar when stood on its end is 8.25 inches. What is the volume of the chocolate package?
In this concept, you will learn how to calculate the volume of a triangular prism.
Finding the Volume of a Triangular Prism
With a triangular prism, the two parallel faces are triangles and the other faces are rectangles.

You calculate the volume of triangular prisms almost the same way that you find the volume of rectangular prisms. You still use the formula \(V=Bh\). However, this time the base of the prism is a triangle, not a rectangle. Therefore, you need to use the area formula for a triangle to find the area of the base, \(B\). Then you can multiply this amount by the height of the rectangle to find the volume of the triangular prism.
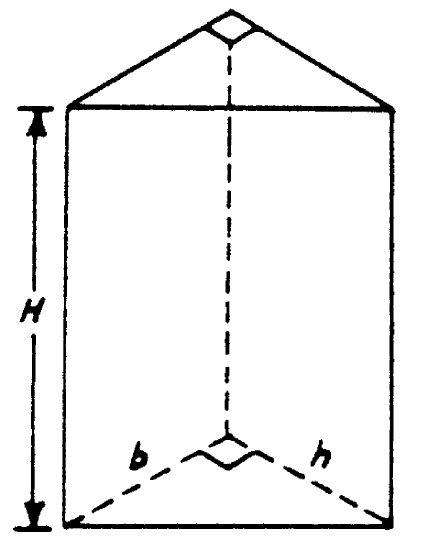
Let’s look at an example.
What is the volume of this triangular prism where the height of the triangular base is 7 cm and the width of the base of the triangle is 5 cm?
First ,you need to find the area of the triangular base. You use the formula for the area of a triangle which is \(\dfrac{1}{2} bh\). Remember, you use the height and base measurements for the triangular face, not the height, H, measurement for the whole prism which is the length of the rectangle.
So there are two things that you need to accomplish: You need to find the area of one of the triangular bases, and then you can take that measurement and multiply it with the height of the entire prism.
\(\begin{aligned} V&=BH \\ b&=\dfrac{1}{2} bh \\ b&=\dfrac{1}{2}(5)(7) \\ b&=35 \\ V&=(35)H \\ V&=(35)(12) \\ V&=420\text{ cm}^{3}\end{aligned}\)
The answer is the volume of this triangular prism is \(420 \text{centimeters}^{3}\).
Example \(\PageIndex{1}\)
Earlier, you were given a problem about how Maggie wants to find the volume of chocolate that will fit inside the packaging.
The triangular base is 1.4 inches; the height of the triangle is 1.25 inches, and the height of the bar when stood on its end is 8.25 inches.
Solution
First, plug in the values for the area formula of a triangle to find the base area, B.
\(\begin{aligned} b&=\dfrac{1}{2} bh \\ b&=\dfrac{1}{2}(1.4)(1.25) \\ b&=0.7(1.25)\\ b&=0.88\text{ in}^{2}\end{aligned} \)
Next, plug the triangle area value, B, and the value for the height of the prism, H, into the volume formula and multiply the values together.
\(\begin{aligned} V&=BH \\ V&=0.88\times 8.25 \\ V&=0.88 \times 8.25 \\ V&=7.26\end{aligned}\)
Then, record the answer, making sure to include the appropriate unit of measurement.
\(V=7.26\text{ in}^{3} \)
The answer is the package has a volume of 7.26 cubic inches.
Example \(\PageIndex{2}\)
Every year Jeanie gets a bottle of her favorite perfume for her birthday. The perfume comes in a bottle shaped like a triangular prism. How much perfume does the bottle hold when it is full?
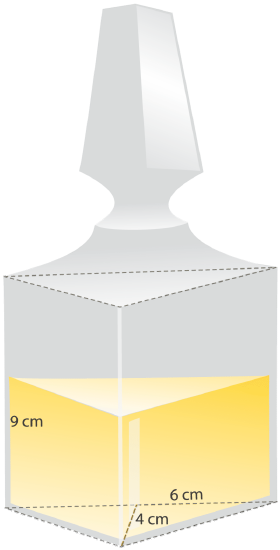
Solution
First, plug in the values for the area formula of a triangle to find the base area, B.
\(\begin{aligned} b&=\dfrac{1}{2} bh \\ b&=\dfrac{1}{2}(6)(4) \\b&=3(4) \\ b&=12\text{ cm}^{2}\end{aligned}\)
Next, plug the triangle area value, B, and the value for the height of the prism, H, into the volume formula and multiply the values together.
\(\begin{aligned} V&=BH \\ V&=12\times 9 \\ V&=12 \times 9 \\ V&=108\end{aligned}\)
Then, record the answer, making sure to include the appropriate unit of measurement.
\(V=108\text{ cm}^{3}\)
The answer is the perfume bottle holds 108 cubic centimeters of perfume when full.
Example \(\PageIndex{3}\)
What is the volume of a triangular prism with the following dimensions: \(b=12\text{ in}\), \(h=10\text{ in}\), \(h=15\text{ in}\)
Solution
First, plug in the values for the area formula of a triangle to find the base area, B\).
\(\begin{aligned} b&=\dfrac{1}{2} bh \\ b&=\dfrac{1}{2}(12)(10) \\ b&=6(10) \\ b&=60\text{ in}^{2}\end{aligned}\)
Next, plug the triangle area value, B, and the value for the height of the prism, H, into the volume formula and multiply the values together.
\(\begin{aligned} V&=BH \\ V&=60\times 15 \\ V&=60 \times 15 \\ V&=900\end{aligned}\)
Then, record the answer, making sure to include the appropriate unit of measurement.
\(V=900\text{ in}^{3}\)
The answer is the volume of this triangular prism is \(900\text{ in}^{3}\).
Example \(\PageIndex{4}\)
What is the volume of a triangular prism with the following dimensions: \(b=7\text{ cm}\), \(h=5\text{ cm}\), \(h=9\text{ cm}\)
Solution
First, plug in the values for the area formula of a triangle to find the base area, B.
\(\begin{aligned}b&=\dfrac{1}{2} bh \\ b&=\dfrac{1}{2}(7)(5) \\ b&=3.5(5) \\ b&=17.5 cm^{2}\end{aligned}\)
Next, plug the triangle area value, B, and the value for the height of the prism, H, into the volume formula and multiply the values together. V\(V=B\(h=17.5\times 9
\(\begin{aligned} V&=17.5 \times 9 \\ V&=157.5 \end{aligned}\)
Then, record the answer, making sure to include the appropriate unit of measurement.
\(V=157.5\text{ cm}^{3}\)
The answer is the volume of this triangular prism is \(157.5\text{ cm}^{3}\).
Example \(\PageIndex{5}\)
What is the volume of a triangular prism with the following dimensions: \(b=4\text{ mm}\), \(h=3\text{ mm}\), \(h=5\text{ mm}\)
Solution
First, plug in the values for the area formula of a triangle to find the base area, B
\(\begin{aligned}b&=\dfrac{1}{2} bh \\ b&=\dfrac{1}{2}(4)(3) \\ b&=2(3) \\ b&=6\text{ mm}^{2}\end{aligned}\)
Next, plug the triangle area value, B, and the value for the height of the prism, H, into the volume formula and multiply the values together.
\(\begin{aligned} V&=BH \\ V&=6\times 5 \\ V&=6 \times 5 \\ V&=30 \end{aligned}\)
Last, record the answer, making sure to include the appropriate unit of measurement.
\(V=30\text{ mm}^{3}\)
The answer is the volume of this triangular prism is \(30\text{ mm}^{3}\).
Review
Find the volume of each triangular prism. Remember that h means the height of the triangular base and H means the height of the whole prism.
- \(b=6\text{ in}\), \(h=4\text{ in}\), \(h=5\text{ in}\)
- \(b=7\text{ in}\), \(h=5\text{ in}\), \(h=9\text{ in}\)
- \(b=10\text{ m}\), \(h=8\text{ m}\), \(h=9\text{ m}\)
- \(b=12\text{ m}\), \(h=10\text{ m}\), \(h=13\text{ m}\)
- \(b=8\text{ cm}\), \(h=6\text{ cm}\), \(h=9\text{ cm}\)
- \(b=9\text{ cm}\), \(h=7\text{ cm}\), \(h=8\text{ cm}\)
- \(b=5.5\text{ m}\), \(h=4\text{ m}\), \(h=4\text{ m}\)
- \(b=11\text{ cm}\), \(h=9\text{ cm}\), \(h=8\text{ cm}\)
- \(b=20\text{ ft}\), \(h=17\text{ ft}\), \(h=19\text{ ft}\)
- \(b=20\text{ ft}\), \(h=18\text{ ft}\), \(h=15\text{ ft}\).
- \(b=18\text{ ft}\), \(h=16\text{ ft}\), \(h=17\text{ ft}\).
- \(b=24\text{ ft}\), \(h=21\text{ ft}\), \(h=19\text{ ft}\).
- \(b=24.5\text{ ft}\), \(h=18\text{ ft}\), \(h=16\text{ ft}\).
- \(b=99\text{ ft}\), \(h=80\text{ ft}\), \(h=75\text{ ft}\).
- \(b=100\text{ ft}\), \(h=80\text{ ft}\), \(h=110\text{ ft}\).
Review (Answers)
To see the Review answers, open this PDF file and look for section 10.11.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Cubic Units | Cubic units are three-dimensional units of measure, as in the volume of a solid figure. |
| Prism | A prism is a three-dimensional object with two congruent parallel bases that are polygons. |
| Volume | Volume is the amount of space inside the bounds of a three-dimensional object. |
Additional Resources
Interactive Element
Video: Solid Geometry Volume
Practice: Volume of Triangular Prisms
Real World: Rainbow Connection

