9.16: Surface Area and Volume of Pyramids
- Page ID
- 6228
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Surface area and volume of solids with a base and lateral faces that meet at a common vertex.
Pyramids
A pyramid is a solid with one base and lateral faces that meet at a common vertex. The edges between the lateral faces are lateral edges. The edges between the base and the lateral faces are base edges.
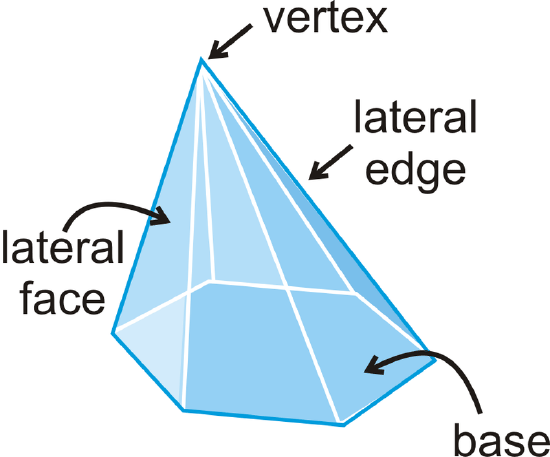
A regular pyramid is a pyramid where the base is a regular polygon. All regular pyramids also have a slant height, which is the height of a lateral face. A non-regular pyramid does not have a slant height.
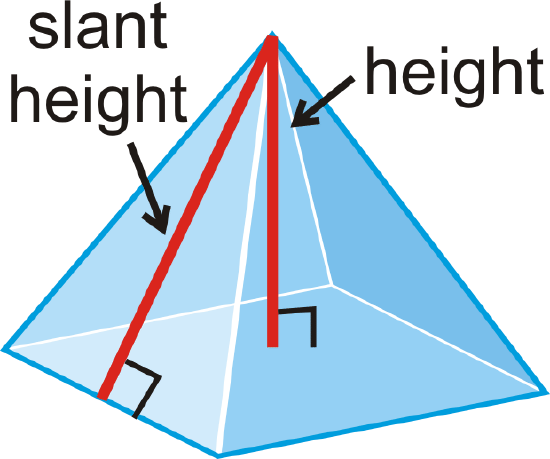
Surface Area
Surface area is a two-dimensional measurement that is the total area of all surfaces that bound a solid. The basic unit of area is the square unit. For pyramids, we will need to use the slant height, which is labeled l, to find the area of each triangular face.
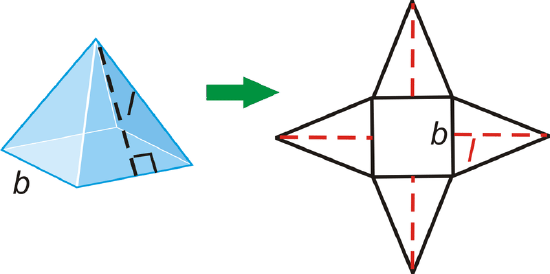
Surface Area of a Regular Pyramid: If B is the area of the base, and n is the number of triangles, then \(SA=B+\dfrac{1}{2}nbl\).
The net shows the surface area of a pyramid. If you ever forget the formula, use the net.
Volume
To find the volume of any solid you must figure out how much space it occupies. The basic unit of volume is the cubic unit.
Volume of a Pyramid: \(V=\dfrac{1}{3}Bh\) where \(B\) is the area of the base.
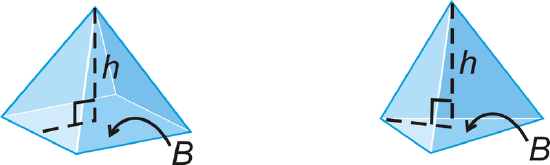
What if you were given a solid three-dimensional figure with one base and lateral faces that meet at a common vertex? How could you determine how much two-dimensional and three-dimensional space that figure occupies?
Example \(\PageIndex{1}\)
Find the slant height of the square pyramid.
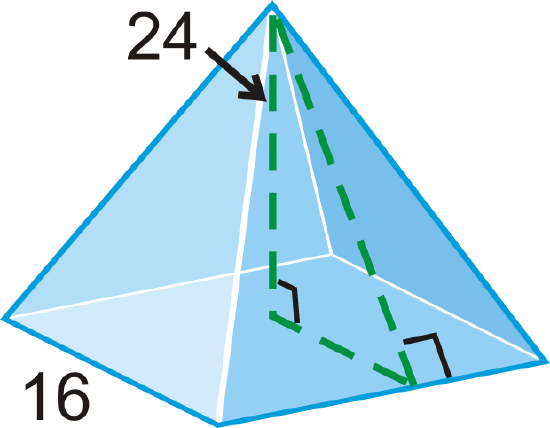
Solution
The slant height is the hypotenuse of the right triangle formed by the height and half the base length. Use the Pythagorean Theorem.
\(\begin{aligned} 8^{2}+24^{2}&=l^{2} \\ 640&=l^{2} \\ l=\sqrt{640}&=8\sqrt{10}\end{aligned}\)
Example \(\PageIndex{2}\)
Find the surface area of the regular triangular pyramid.
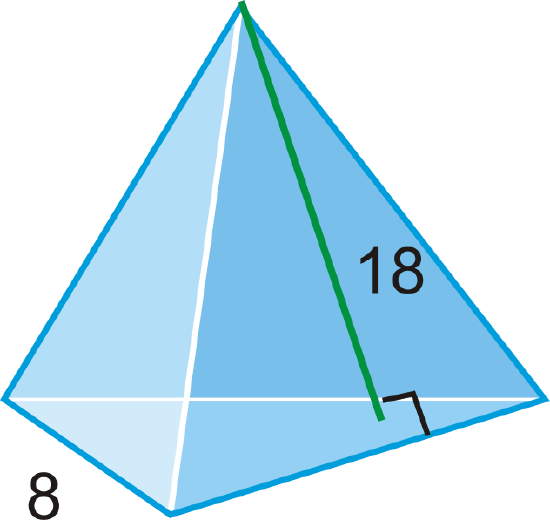
Solution
“Regular” tells us the base is an equilateral triangle. Let’s draw it and find its area.
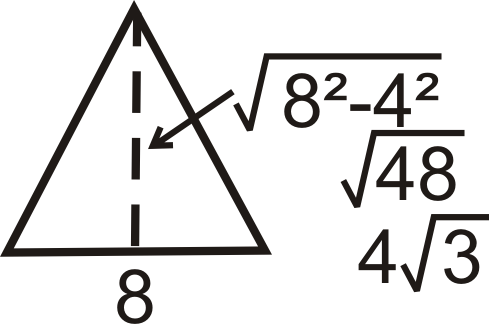
\(B=\dfrac{1}{2}\cdot 8\cdot 4\sqrt{3}=16\sqrt{3}\)
The surface area is:
\(SA=16\sqrt{3}+\dfrac{1}{2}\cdot 3\cdot 8\cdot 18=16\sqrt{3}+216\approx 243.71\)
Example \(\PageIndex{3}\)
If the lateral surface area of a regular square pyramid is \(72\: ft^{2}\) and the base edge is equal to the slant height. What is the length of the base edge?
Solution
In the formula for surface area, the lateral surface area is \(\dfrac{1}{2}nbl\). We know that \(n=4\) and \(b=l\). Let’s solve for \(b\).
\(\begin{aligned} \dfrac{1}{2}nbl&=72\text{ ft}^{2} \\ \dfrac{1}{2}(4)b^{2}&=7^{2} \\ 2b^{2}&=7^{2} \\ b^{2}&=36\\ b&=6 \text{feet}\end{aligned}\)
Example \(\PageIndex{4}\)
Find the height and then volume of the pyramid.
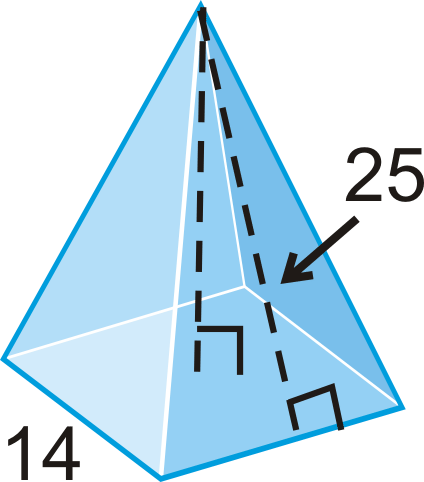
Solution
In this example, we are given the slant height. Use the Pythagorean Theorem.
\(\begin{aligned} 7^{2}+h^{2}&=25^{2} \\ h^{2}&=576 \\ h&=24\end{aligned}\)
\(V=13(142)(24)=1568\text{ units}^{3}\)
Example \(\PageIndex{5}\)
Find the volume of the pyramid with a right triangle as its base.
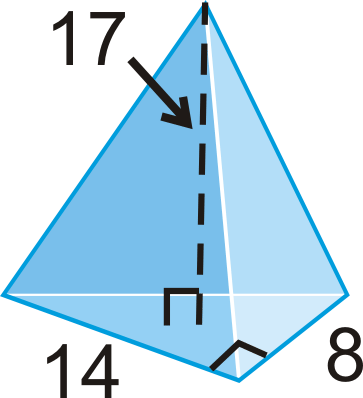
Solution
The base of the pyramid is a right triangle. The area of the base is \(\dfrac{1}{2}(14)(8)=56\text{ units}^{2}\).
\(V=\dfrac{1}{3}(56)(17)\approx 317.33\text{ units}^{3}\)
Example \(\PageIndex{6}\)
A rectangular pyramid has a base area of \(56\: cm^{2}\) and a volume of \(224\: cm^{3}\). What is the height of the pyramid?
Solution
Use the formula for volume and plug in the information we were given. Then solve for the height.
\(\begin{aligned} V&=\dfrac{1}{3}Bh \\ 224&=\dfrac{1}{3}\cdot 56h \\ 12&=h \end{aligned}\)
Review
Fill in the blanks about the diagram to the left.
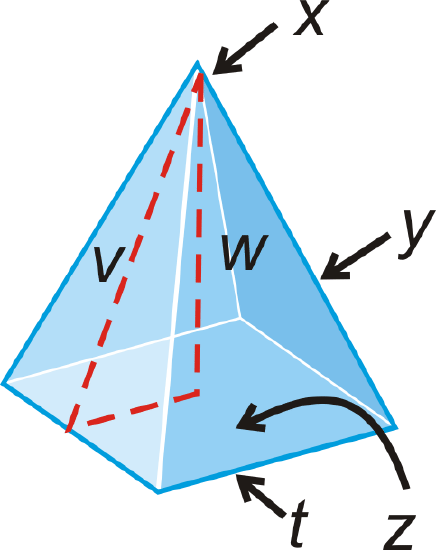
- x is the ___________.
- The slant height is ________.
- y is the ___________.
- The height is ________.
- The base is _______.
- The base edge is ________.
For questions 7-8, sketch each of the following solids and answer the question. Your drawings should be to scale, but not one-to-one. Leave your answer in simplest radical form.
- Draw a square pyramid with an edge length of 9 in and a 12 in height. Find the slant height.
- Draw an equilateral triangle pyramid with an edge length of 6 cm and a height of 6 cm. What is the height of the base?
Find the slant height, l, of one lateral face in each pyramid. Round your answer to the nearest hundredth.
-
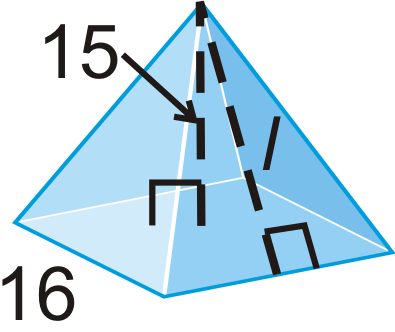
Figure \(\PageIndex{11}\) -
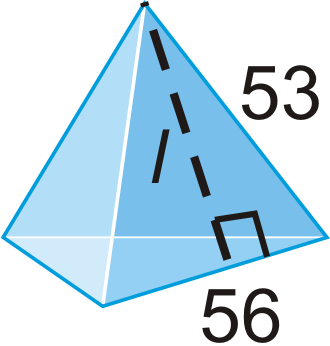
Figure \(\PageIndex{12}\)
Find the surface area and volume of the regular pyramid. Round your answers to the nearest hundredth.
-
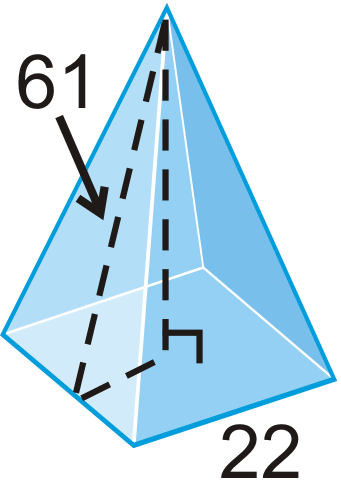
Figure \(\PageIndex{13}\) -
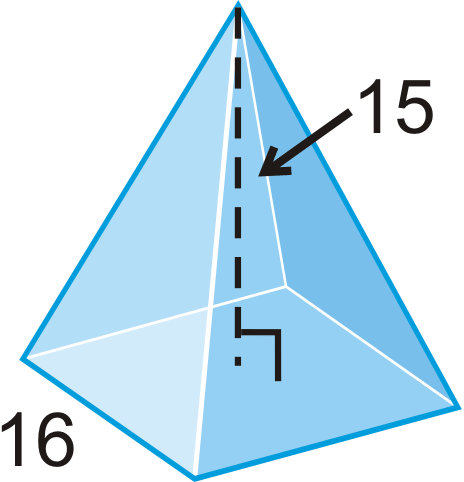
Figure \(\PageIndex{14}\) -
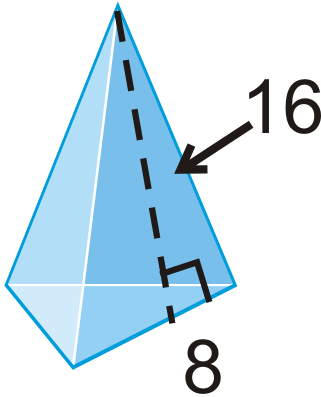
Figure \(\PageIndex{15}\) -
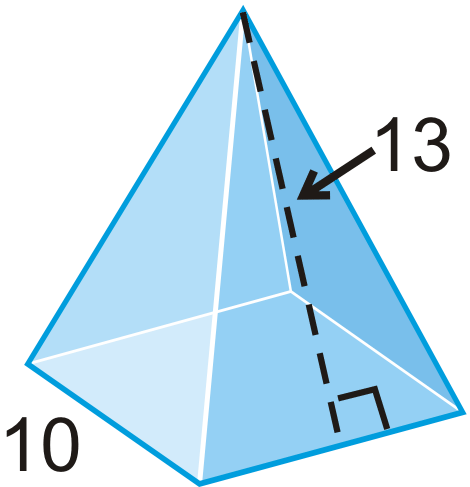
Figure \(\PageIndex{16}\) -
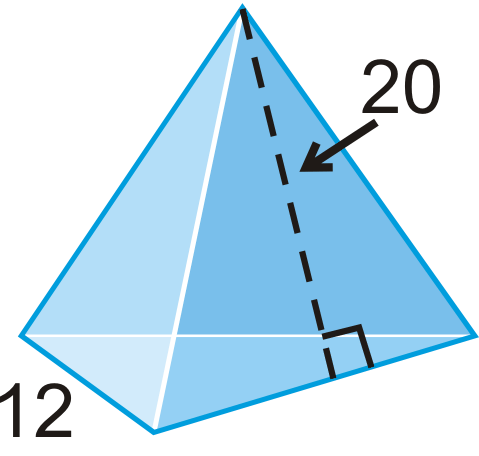
Figure \(\PageIndex{17}\) -
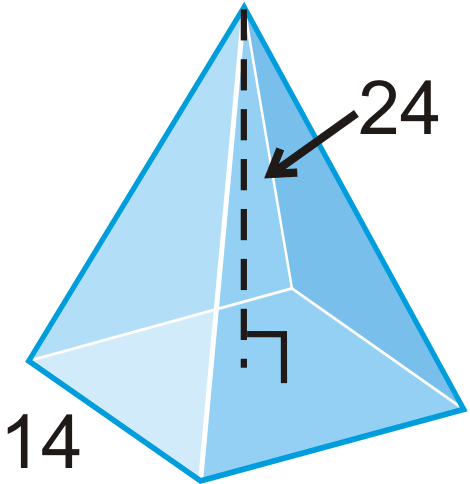
Figure \(\PageIndex{18}\) - A regular tetrahedron has four equilateral triangles as its faces.
- Find the height of one of the faces if the edge length is 6 units.
- Find the area of one face.
- Find the total surface area of the regular tetrahedron.
- If the surface area of a square pyramid is \(40\text{ ft}^{2}\) and the base edge is 4 ft, what is the slant height?
- If the lateral area of a square pyramid is \(800\text{ in}^2\) and the slant height is 16 in, what is the length of the base edge?
- If the lateral area of a regular triangle pyramid is \(252\text{ in}^2\) and the base edge is 8 in, what is the slant height?
- The volume of a square pyramid is 72 square inches and the base edge is 4 inches. What is the height?
- The volume of a triangle pyramid is \(170\text{ in}^3\) and the base area is \(34\text{ in}^2\). What is the height of the pyramid?
Review (Answers)
To see the Review answers, open this PDF file and look for section 11.5.
Vocabulary
| Term | Definition |
|---|---|
| lateral edges | Edges between the lateral faces of a prism. |
| lateral faces | The non-base faces of a prism. |
| Pyramid | A pyramid is a three-dimensional object with a base that is a polygon and triangular faces that meet at one vertex. |
| regular pyramid | is a pyramid where the base is a regular polygon. All regular pyramids also have a slant height, which is the height of a lateral face. |
| Cone | A cone is a solid three-dimensional figure with a circular base and one vertex. |
| Vertex | A vertex is a point of intersection of the lines or rays that form an angle. |
| Volume | Volume is the amount of space inside the bounds of a three-dimensional object. |
| Cavalieri's Principle | States that if two solids have the same height and the same cross-sectional area at every level, then they will have the same volume. |
| Base Edge | The base edge is the edge between the base and the lateral faces of a prism. |
| Slant Height | The slant height is the height of a lateral face of a pyramid. |
| Apothem | The apothem of a regular polygon is a perpendicular segment from the center point of the polygon to the midpoint of one of its sides. |

