9.17: Volume of Pyramids
- Page ID
- 6269
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Volume equals area of the base times \(\dfrac{1}{3}\) of height.

Michael and Juanita are interested in the amount of sand required to build a sand pyramid of the size that they see while at a sand sculpture exhibit. They carefully measure the width of the square base of the sand pyramid which is 4 feet and the height of the pyramid which is 5 feet. How much sand is required to build this sand pyramid?
In this concept, you will learn how to calculate the volume of a pyramid.
Finding the Volume of a Pyramid
Pyramids are solid shapes that exist in three-dimensional space. A pyramid has sides that are triangular faces and a base that can be any shape.

Volume is the measure of how much space a three-dimensional figure takes up or holds. Volume is measured in cubic units, because you are dealing with three dimensions: length, width, and height.
You can start to understand the volume of a pyramid by comparing a pyramid with a figure that is similar to it. You know that a prism has length, width and height. The parallel bases of a prism can be any polygon. This one has a square base; so it is called a cube.
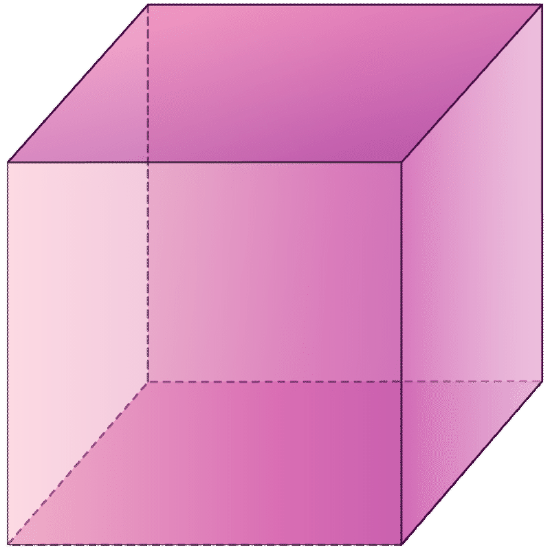
Now think about a pyramid. It has a base that can be any polygon. The base of this pyramid is a square.
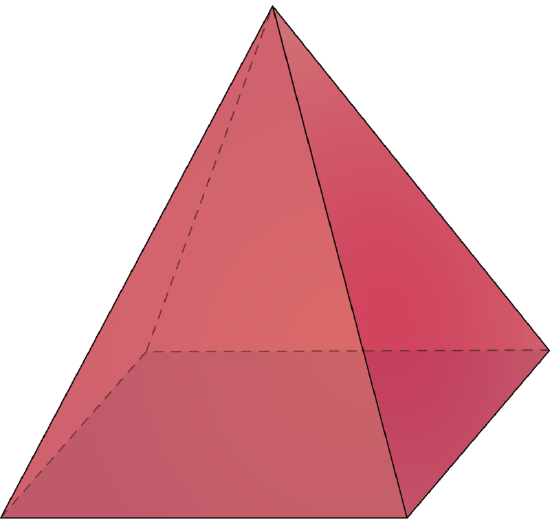
These are both similar given that they have square bases. Think about the volume of a pyramid by looking at the volume of the cube or prism. Look at this picture that demonstrates the relationship of a cube to a square pyramid:

To find the volume of this cube, multiply the base times the width times the height. To find the volume of the pyramid, take the area of the base, \(B\) and multiply it times the height and then multiply it by \(\dfrac{1}{3}\). Here is the formula for finding the volume of a pyramid.
\(\(V=\dfrac{1}{3}Bh\)
One thing to keep in mind is that pyramids can be tricky because they can have many different bases. \(B\) in the formula means that you need to find the area of the base. If the base is a square, you will need to use the formula for area of a square, \(B=s^2\). If the base is a rectangle, the area of the base is \(B=lw\). If the base is a triangle, use the formula \(B=\dfrac{bh}{2}\). Making sure that you have the correct formula is essential in your work with pyramids.
Let's look at an example. What is the volume of the pyramid below?
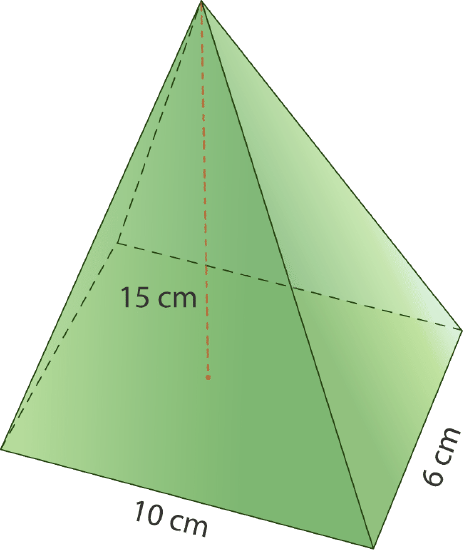
First, decide what shape the base of the pyramid is. One side is 10 centimeters and the other is 6 centimeters, so it must be a rectangle. Use the area formula for rectangles to find B, the base area.
\(\begin{aligned} B&=lw \\ B&=10(6) \\ B&=60\text{ cm}^{2}\end{aligned}\)
The area of this pyramid’s base is 60 square centimeters. Now multiply this by the height and 13 according to the formula.
\(\begin{aligned} V&=\dfrac{1}{3}Bh \\ V&=\dfrac{1}{3}(60)(15) \\ V&=\dfrac{900}{3} \\ V&=300\text{ cm}^{3}\end{aligned}\)
The answer is the volume of the pyramid is 300 cubic centimeters.
Remember, you measure volume in three dimensions, so write the answer in cubic units.
Let's look at another example.
Find the volume of the figure below.
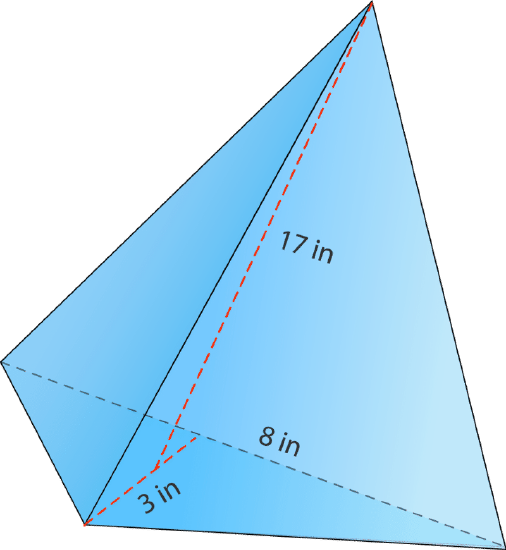
This time the base is a triangle, so you'll need to use the area formula for triangles to find the base area. Be careful not to confuse the height of the base triangle with the height of the whole pyramid.
\(\begin{aligned} B&=\dfrac{1}{2}bh\\ B&=\dfrac{1}{2}(8)(3) \\ B&=\dfrac{24}{2} \\ B&=12 in^{2}\end{aligned}\)
The base area for this triangular pyramid is 12 square inches. Put this into the formula and solve for V, volume.
\(\begin{aligned} V&=\dfrac{1}{3}Bh \\ V&=\dfrac{1}{3}(12)(17) \\ V&=\dfrac{204}{3} \\ V&=68\text{ in}^{3}\end{aligned}\)
The answer is the volume of this pyramid is 68 cubic inches.
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Michael and Juanita's interest in the sand sculpture pyramid.
They want to figure out the volume of sand required to create a sand sculpture pyramid with base 4 feet and height 5 feet:
Solution
First, determine the shape of the base and use the correct formula to find the base area. Since the base is a square, use the area formula for squares to find the base area.
\(\begin{aligned} B&=s^{2} \\ B&=(4)^{2} \\ B&=16\text{ ft}^{2}\end{aligned}\)
The base area of the pyramid is 16 square centimeters.
Next, plug the area of the base, and the height of the pyramid into the formula for volume of a pyramid and multiply the values together.
\(\begin{aligned} V&=\dfrac{1}{3}Bh \\ V&=\dfrac{1}{3}(16)(5) \\ V&=803\end{aligned}\)
Then, divide by 3 for the answer, making sure to include the appropriate unit of measurement.
\(\begin{aligned}V&=803 \\ V&=26.67\text{ ft}^{3}\end{aligned}\)
The answer is the volume of sand required to create the sand sculpture pyramid is 26.67 cubic feet.
Example \(\PageIndex{2}\)
Felice bought the candle below for her friend’s birthday. The package says that the candle burns one hour for every 20 cubic centimeters of wax. What is the volume of the candle so that Felice can figure out how long it will burn?
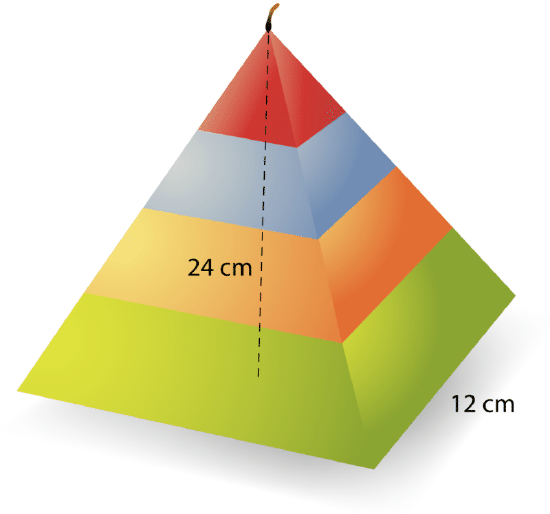
Solution
First, determine the shape of the base and use the correct formula to find the base area. Since the base is a square, you use the area formula for squares to find the base area.
\(\begin{aligned}B&=s^{2} \\ B&=(12)^{2} \\ B&=144\text{ cm}^{2}\end{aligned}\)
The base area of the pyramid is 144 square centimeters.
Next, plug the area of the base, and the height of the pyramid into the formula for volume of a pyramid and multiply the values together.
\(\begin{aligned} V&=\dfrac{1}{3}Bh \\ V&=\dfrac{1}{3}(144)(24) \\ V&=\dfrac{3456}{3}\end{aligned}\)
Then, divide by 3 for the answer, making sure to include the appropriate unit of measurement.
\(\begin{aligned} V&=\dfrac{3456}{3} \\ V&=1,152\text{ cm}^{3}\end{aligned}\)
The answer is the volume of the candle is 1,152 cubic cm.
Example \(\PageIndex{3}\)
Find the volume of a square pyramid with a base of 8 cm and a height of 6 cm.
Solution
First, determine the shape of the base and use the correct formula to find the base area. The base is a square, so use the area formula for squares to find the base area.
\(\begin{aligned} B&=s^{2} \\ B&=(8)^{2} \\ B&=64\text{ cm}^{2}\end{aligned}\)
The base area of the pyramid is 64 square centimeters.
Next, plug the area of the base, and the height of the pyramid into the formula for volume of a pyramid and multiply the values together.
\(\begin{aligned} V&=\dfrac{1}{3}Bh \\ V&=\dfrac{1}{3}(64)(6) \\ V&=\dfrac{384}{3}\end{aligned} \)
Then, divide by 3 for the answer, making sure to include the appropriate unit of measurement.
\(\begin{aligned} V&=\dfrac{384}{3} \\ V&=128\text{ cm}^{3}\end{aligned}\)
The answer is the volume of the pyramid is 128 cubic cm.
Example \(\PageIndex{4}\)
Find the volume of a rectangular pyramid with a length of 10 cm, a width of 8 cm and a height of 9 cm.
Solution
First, determine the shape of the base and use the correct formula to find the base area. Since the base is a rectangle, use the area formula for squares to find the base area.
\(\begin{aligned} B&=lw \\ B&=(10)(8) \\ B&=80\text{ cm}^{2}\end{aligned}\)
The base area of the pyramid is 80 square centimeters.
Next, plug the area of the base, and the height of the pyramid into the formula for volume of a pyramid and multiply the values together.
\(\begin{aligned} V&=\dfrac{1}{3}Bh \\ V&=\dfrac{1}{3}(80)(9) \\ V&=\dfrac{720}{3}\end{aligned}\)
Then, divide by 3 for the answer, making sure to include the appropriate unit of measurement.
\(\begin{aligned} V&=\dfrac{720}{3} \\ V&=240\text{ cm}^{3}\end{aligned}\)
The answer is the volume of the pyramid is 240 cubic cm.
Example \(\PageIndex{5}\)
Find the volume of a square pyramid with a base of 5.5 in and a height of 4 in.
Solution
First, determine the shape of the base and use the correct formula to find the base area. The base is a square, so use the area formula for squares to find the base area.
\(\begin{aligned} B&=s^{2} \\ B&=(5.5)^{2} \\ B&=30.25 in^{2}\end{aligned} \)
The base area of the pyramid is 30.25 square centimeters.
Next, plug the area of the base, and the height of the pyramid into the formula for volume of a pyramid and multiply the values together.
\(\begin{aligned} V&=\dfrac{1}{3}Bh \\ V&=\dfrac{1}{3}(30.25)(4) \\ V&=\dfrac{121}{3}\end{aligned}\)
Then, divide by 3 for the answer, making sure to include the appropriate unit of measurement.
\(\begin{aligned} V&=\dfrac{121}{3} \\ V&=40.33\text{ in}^{3}\end{aligned}\)
The answer is the volume of the pyramid is 40.33 cubic inches.
Review
Find the volume of each of the following pyramids.
- A square pyramid with a base of 6 ft and a height of 9 ft.
- A square pyramid with a base of 8 m and a height of 10 m.
- A square pyramid with a base of 11 in and a height of 13 in.
- A square pyramid with a base of 9 ft and a height of 14 ft.
- A square pyramid with a base of 4.5 in and a height of 5 inches.
- A rectangular pyramid with a base length of 4 in, a base width of 3 in and a height of 5 in.
- A rectangular pyramid with a base length of 5 ft, a base width of 4 ft and a height of 6 ft.
- A rectangular pyramid with a base length of 7 m, a base width of 4 m and a height of 9 m.
- A triangular pyramid with a base length of 5 in and a base height of 4 inches with a pyramid height of 6 inches.
- A triangular pyramid with a base length of 8 ft and a base height of 7 ft with a pyramid height of 9 ft.
- A square pyramid with a base of 8 feet and height of 4 feet.
- A rectangular pyramid with a length of 5 inches, a width of 4 inches and a height of 6 inches.
- A square pyramid with a base of 3.5 feet and a height of 6.5 feet.
- A square pyramid with a base of 6.5 feet and a height of 8.5 feet.
- A rectangular pyramid with a width of 4 feet, a length of 6 feet and a height of 7.5 feet.
Review (Answers)
To see the Review answers, open this PDF file and look for section 10.14.
Vocabulary
| Term | Definition |
|---|---|
| Cone | A cone is a solid three-dimensional figure with a circular base and one vertex. |
| Pyramid | A pyramid is a three-dimensional object with a base that is a polygon and triangular faces that meet at one vertex. |
| Volume | Volume is the amount of space inside the bounds of a three-dimensional object. |
Additional Resources
Interactive Element
Video: Volume of a Pyramid - Overview
Practice: Volume of Pyramids

