9.18: Surface Area and Volume of Cylinders
- Page ID
- 6288
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Surface area and volume of solids with congruent circular bases in parallel planes.
Cylinders
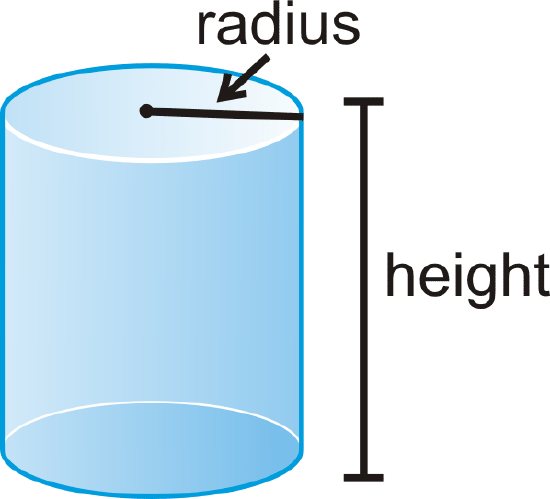
A cylinder is a solid with congruent circular bases that are in parallel planes. The space between the circles is enclosed.
A cylinder has a radius and a height.
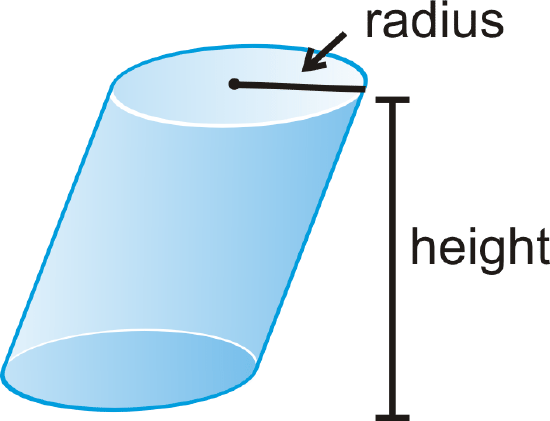
A cylinder can also be oblique (slanted) like the one below.
Surface Area
Surface area is the sum of the area of the faces of a solid. The basic unit of area is the square unit.
Surface Area of a Right Cylinder: \(SA=2 \pi r^{2}+2 \pi r h\).
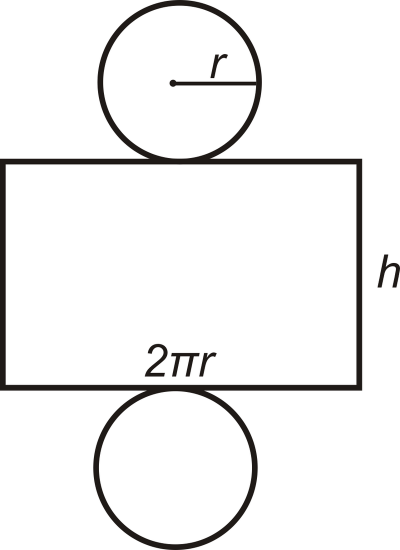
\(\underbrace{2 \pi r^{2}}_\text{area of both circles}+ \underbrace{2 \pi r h}_\text{length of rectangle}\)
Volume
To find the volume of any solid you must figure out how much space it occupies. The basic unit of volume is the cubic unit. For cylinders, volume is the area of the circular base times the height.
Volume of a Cylinder: \(V= \pi r^{2}h\)
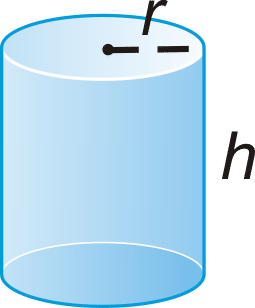
If an oblique cylinder has the same base area and height as another cylinder, then it will have the same volume. This is due to Cavalieri’s Principle, which states that if two solids have the same height and the same cross-sectional area at every level, then they will have the same volume.
What if you were given a solid three-dimensional figure with congruent enclosed circular bases that are in parallel planes? How could you determine how much two-dimensional and three-dimensional space that figure occupies?
Example \(\PageIndex{1}\)
If the volume of a cylinder is \(484 \pi in^{3}\) and the height is 4 in, what is the radius?
Solution
Solve for \(r\).
\(\begin{aligned} 484 \pi&= \pi r^{2}(4) \\ 121&=r^{2} \\ 11\text{ in}&=r\end{aligned}\)
Example \(\PageIndex{2}\)
The circumference of the base of a cylinder is \(80 \pi\) cm and the height is 36 cm. Find the total surface area.
Solution
We need to solve for the radius, using the circumference.
\(\begin{aligned} 2 \pi r&=80 \pi \\ r&=40\end{aligned}\)
Now, we can find the surface area.
\(\begin{aligned} SA&=2 \pi(40)^{2}+(80 \pi)(36) \\ &=3200 \pi+2880 \pi \\ &=6080 \pi \text{ units}^{2}\end{aligned}\)
Example \(\PageIndex{3}\)
Find the surface area of the cylinder.
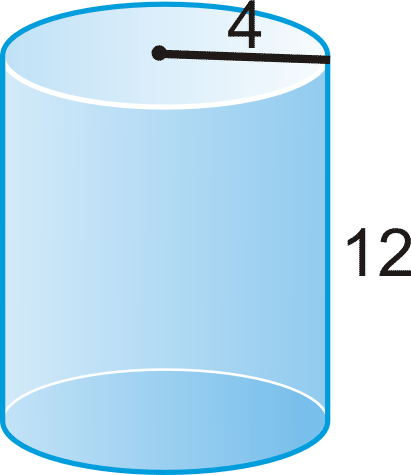
Solution
\(r=4\) and \(h=12\).
\(\begin{aligned} SA&=2 \pi(4)^{2}+2 \pi(4)(12) \\ &=32 \pi+96 \pi \\ &=128 \pi \text{ units}^{2}\end{aligned} \)
Example \(\PageIndex{4}\)
The circumference of the base of a cylinder is \(16 \pi\) and the height is 21. Find the surface area of the cylinder.
Solution
We need to solve for the radius, using the circumference.
\(\begin{aligned} 2 \pi r&=16 \pi \\ r&=8\end{aligned}\)
Now, we can find the surface area.
\(\begin{aligned} SA&=2 \pi(8)2+(16 \pi)(21) \\ &=128 \pi+336 \pi \\ &=464 \pi \text{ units}^{2}\end{aligned}\)
Example \(\PageIndex{5}\)
Find the volume of the cylinder.
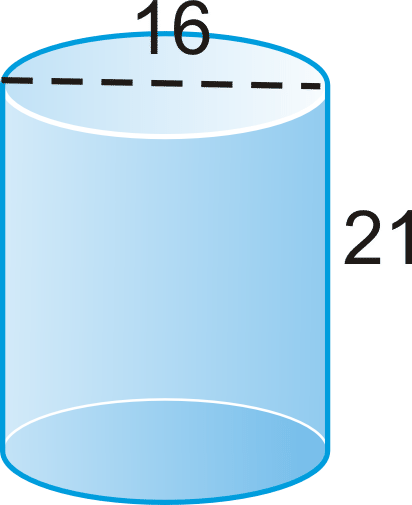
Solution
If the diameter is 16, then the radius is 8.
\(\begin{aligned} V&= \pi 8^{2}(21) \\ &=1344 \pi \text{ units}^{3}\end{aligned}\)
Review
- Two cylinders have the same surface area. Do they have the same volume? How do you know?
- A cylinder has \(r=h\) and the radius is 4 cm. What is the volume?
- A cylinder has a volume of \(486 \pi \text{ ft}^{3}\). If the height is 6 ft., what is the diameter?
- A right cylinder has a 7 cm radius and a height of 18 cm. Find the volume.
Find the volume of the following solids. Round your answers to the nearest hundredth.
-
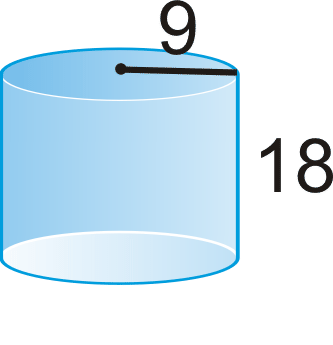
Figure \(\PageIndex{7}\) -

Figure \(\PageIndex{8}\)
Find the value of x, given the volume.
- \(V=6144 \pi \text{ units}^{3}\)
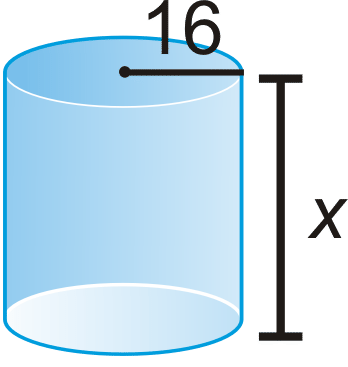
Figure \(\PageIndex{9}\) - The area of the base of a cylinder is \(49 \pi \text{ in}^{2}\) and the height is 6 in. Find the volume.
- The circumference of the base of a cylinder is \(34 \pi \text{ cm}\) and the height is 20 cm. Find the total surface area.
- The lateral surface area of a cylinder is \(30 \pi \text{ m}^{2}\) and the height is 5 m. What is the radius?
Review (Answers)
To see the Review answers, open this PDF file and look for section 11.4.
Vocabulary
| Term | Definition |
|---|---|
| cylinder | A solid with congruent circular bases that are in parallel planes. The space between the circles is enclosed. A cylinder has a radius and a height and can also be oblique (slanted). |
| Surface Area | Surface area is the total area of all of the surfaces of a three-dimensional object. |
| Volume | Volume is the amount of space inside the bounds of a three-dimensional object. |
| Cavalieri's Principle | States that if two solids have the same height and the same cross-sectional area at every level, then they will have the same volume. |
| Oblique Cylinder | An oblique cylinder is a cylinder with bases that are not directly above one another. |
Additional Resources
Interactive Element
Video: Cylinders Principles - Basic
Activities: Cylinders Discussion Questions
Study Aids: Prisms and Cylinders Study Guide
Practice: Surface Area and Volume of Cylinders
Real World: Drill Teams

