9.19: Surface Area of Cylinders
- Page ID
- 6289
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)\(SA=2 \pi r(h+r)\)
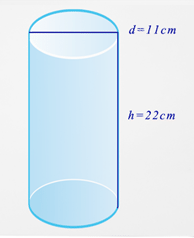
Mrs. Johnson is wrapping a cylindrical package in brown paper so that she can mail it to her son. Based on the dimensions shown, how much paper will she need to cover the package?
In this concept, you will learn to find the surface area of cylinders.
Surface Area
A cylinder has two parallel congruent circular bases with a curved rectangle as its side. One way is to use a net.
A net is a two-dimensional diagram of a three-dimensional figure. If you could unfold a cylinder (like a can) so that it is completely flat, you would have something that looks like this.
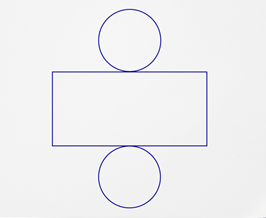
With the net of a cylinder, you would need to calculate the area of each circle and the area of the curved side of the cylinder. Then you could add these values together to find the k.
The formula \(A&= \pi r^{2}\) can be used to find the area of a circle bases. Look closely again at the cylinder above. The two circular faces are congruent, so they must have the same radius and diameter.
Let’s look at an example.
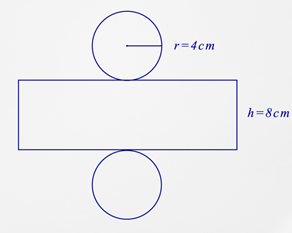
First, calculate the area of the circular bases.
\(\begin{aligned} A&= \pi r^{2}\\ A&= \pi (4)^{2} \\ A&= \pi (16) \\ A&=50.3\end{aligned}\)
Next, find the length of the cylinder’s side. You know the width is 8 cm but the length is not shown. The cylinder was unwrapped to form the net. Therefore, the circumference of the circle would be the length of the side.
\(\begin{aligned}C&=2 \pi r \\ C&=2 \pi \times 4 \\ C&=25.1\end{aligned}\)
Then, calculate the area of the side.
\(\begin{aligned}A&=l\times w \\ A&=25.1\times 8 \\ A&=200.8\end{aligned}\)
Then, find the surface area of the cylinder by adding the side area to the top and bottom area.
\(\begin{aligned}SA&=bottom+top+side \\ SA&=50.3+50.3+200.8 \\ SA&=301.4\end{aligned}\)
The answer is 301.4.
The surface area of the cylinder is \(301.4 \text{ cm}^{2}\).
Putting this all together, you can use the following formula to find the surface area of the cylinder:
\(SA=2 \pi r^{2}+2 \pi rh\)
The formula \(2 \pi r^{2}\) represents the area of the top and bottom circles of the cylinder. The \(2 \pi r h\) represents the perimeter (\(2 \pi r\)) multiplied by the height, \(h\).
Let’s look at an example.
What is the surface area of the figure below?
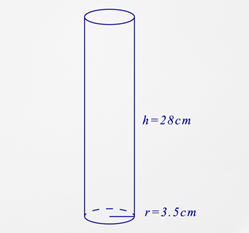
First, substitute what you know into the surface area formula.
\(\begin{aligned}SA&=2 \pi r^{2}+2 \pi r h \\ SA&=2 \pi (3.5)^{2}+2 \pi (3.5)(28)\end{aligned}\)
Next, calculate the surface area.
\(\begin{aligned}SA&=2 \pi (3.5)^{2}+2 \pi (3.5)(28) \\ SA&=2 \pi (12.25)+2 \pi (98) \\ SA&=76.97+615.75 \\ SA&=692.72\end{aligned}\)
The answer is 692.72.
The surface area of the cylinder is \(692.7 \text{ cm}^{2}\).
Sometimes, you can have a cylinder that has been cut. This is called a truncated cylinder. This is where you only see a section of the cylinder and will need to figure out the surface area of what you see.
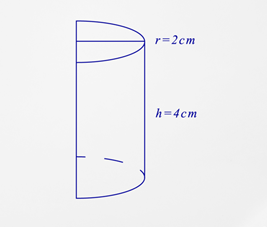
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Mrs. Johnson’s cylindrical wrapping.
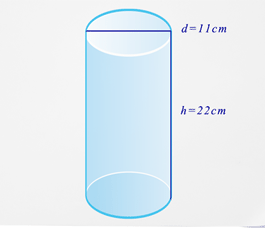
Solution
First, you need to find the radius. Remember, the radius is half the measure of the diameter.
\(\begin{aligned}r&=\dfrac{d}{2} \\ r&=\dfrac{11}{2} \\ r&=5.5v\end{aligned}\)
Next, substitute what you know into the surface area formula.
\(\begin{aligned}SA&=2 \pi r^{2}+2 \pi rh \\ SA&=2 \pi (5.5)^{2}+2 \pi (5.5)(22)\end{aligned}\)
Then, calculate the surface area.
\(\begin{aligned}SA&=2 \pi (5.5)^{2}+2 \pi (5.5)(22) \\ SA&=2 \pi (30.25)+2 \pi (121) \\ SA&=190.1+760.3 \\ SA&=950.4\end{aligned}\)
The answer is 950.4.
Mrs. Johnson needs \(950.4 \: cm^{2}\) of brown paper to wrap her parcel.
Example \(\PageIndex{2}\)
What is the surface area of the figure below?
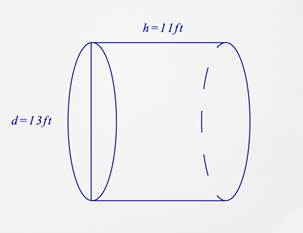
Solution
First, you need to find the radius. Remember that the radius is half the measure of the diameter.
\(\begin{aligned}r&=\dfrac{d}{2} \\ r&=\dfrac{13}{2} \\ r&=6.5\end{aligned}\)
Next, substitute what you know into the surface area formula.
\(\begin{aligned}SA&=2 \pi r^{2}+2 \pi rh \\ SA&=2 \pi (6.5)^{2}+2 \pi (6.5)(11)\end{aligned}\)
Then, calculate the surface area.
\(\begin{aligned}SA&=2 \pi (6.5)^{2}+2 \pi (6.5)(11) \\ SA&=2 \pi (42.25)+2 \pi (71.5) \\ SA&=265.5+449.2 \\ SA&=714.7\end{aligned}\)
The answer is 714.7.
The surface area of the cylinder is \(714.7 \: ft^{2}.
Example \(\PageIndex{3}\)
Find the surface area of a cylinder with a radius of 6 inches and a height of 5 inches.
Solution
First, substitute what you know into the surface area formula.
\(\begin{aligned}SA&=2 \pi r^{2}+2 \pi rh \\ SA&=2 \pi (6)^{2}+2 \pi (6)(5)\end{aligned}\)
Next, calculate the surface area.
\(\begin{aligned} SA&=2 \pi (6)^{2}+2 \pi (6)(5) \ SA&=2 \pi (36)+2 \pi (30) \\ SA&=226.2+188.5 \\ SA&=414.7\end{aligned}\)
The answer is 414.7.
The surface area of the cylinder is \(414.7 \: in^{2}\).
Example \(\PageIndex{4}\)
Find the surface area of a cylinder with a radius of 4 cm and a height of 12 cm.
Solution
First, substitute what you know into the surface area formula.
\(SA&=2 \pi r^{2}+2 \pi rh \\ SA&=2 \pi (4)^{2}+2 \pi (4)(12)\end{aligned}\)
Next, calculate the surface area.
\(\begin{aligned} SA&=2 \pi (4)^{2}+2 \pi (4)(12) \\ SA&=2 \pi (16)+2 \pi (48) \\ SA&=100.5+301.6 \\ SA&=402.1\end{aligned}\)
The answer is 402.1.
The surface area of the cylinder is \(402.1 \: cm^{2}\).
Example \(\PageIndex{5}\)
Find the surface area of a cylinder with a diameter of 10 meters and a height of 15 meters.
Solution
First, you need to find the radius. Remember that the radius is half the measure of the diameter.
\(\begin{aligned} r&=\dfrac{d}{2} \\ r&=\dfrac{10}{2} \\ r&=5\end{aligned}\)
Next, substitute what you know into the surface area formula.
\(\begin{aligned} SA&=2 \pi r^{2}+2 \pi r h \\ SA&=2 \pi (5)^{2}+2 \pi (5)(15)\end{aligned}\)
Then, calculate the surface area.
\(\begin{aligned}SA&=2 \pi (5)^{2}+2 \pi (5)(15) \\ SA&=2 \pi (25)+2 \pi (75) \\ SA&=157.1+471.2 \\ SA&=628.3\end{aligned}\)
The answer is 628.3.
The surface area of the cylinder is \(628.3 \: m^{2}\).
Review
Use the diagrams to answer the questions below each one.
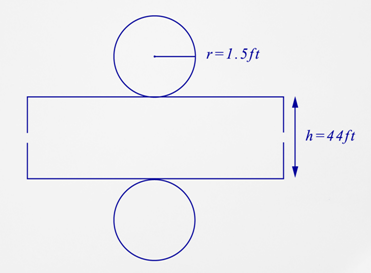
- What is the name of this figure?
- What is the shape of the base of this figure?
- How many bases are there?
- What is the surface area of this figure?
- Which measurement is needed the radius or the diameter?
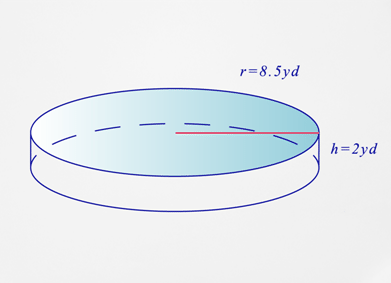
- What is the name of this figure?
- Which measurement is given the radius or the diameter?
- What is the surface area of the figure?
Use what you have learned to answer each question.
- A cylindrical water tank is 35 long and 10 feet across. How much sheet metal is the tank made of?
- Did you use area or surface area to solve this problem?
- True or false. You can only find the surface area if you know the volume.
- True or false. Surface area and volume measure the same thing.
- True or false. Surface area measures the outside of a cylinder.
- True or false. You need the radius to find the surface area of a cylinder.
- True or false. The radius is one-half of the diameter.
Review (Answers)
To see the Review answers, open this PDF file and look for section 8.7.
Vocabulary
| Term | Definition |
|---|---|
| Cylinder | A cylinder is a solid figure with two parallel congruent circular bases. |
| Net | A net is a diagram that shows a “flattened” view of a solid. In a net, each face and base is shown with all of its dimensions. A net can also serve as a pattern to build a three-dimensional solid. |
| Prism | A prism is a three-dimensional object with two congruent parallel bases that are polygons. |
| Surface Area | Surface area is the total area of all of the surfaces of a three-dimensional object. |
| Three – Dimensional | A figure drawn in three dimensions is drawn using length, width and height or depth. |
| Truncated Cylinder | A cylinder that is cut in part from a complete cylinder. |
Additional Resources
Interactive Element
Video: Cylinder Volume and Surface Area
Practice: Surface Area of Cylinders
Real World: Why Do Supertankers Float?

