9.20: Volume of Cylinders
- Page ID
- 6290
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Volume equals the area of top or bottom times height.
Ramona prepared a large pot of fruit preserves, but she ran out of canning jars before she had canned all of the preserves. She took two food storage containers out of the cupboard. The cylindrical containers have the dimensions below. There isn’t enough of the extra preserve for both containers, so she only needs one of the containers and it needs to be the one with the greatest volume.
How can Ramona use these dimensions to figure out which container will hold the most?
In this concept, you will learn to use formulas to find the volume of cylinders.
Finding Volume of Cylinders
Volume is the amount of space contained within a solid figure. In the case of cylinders, you can think of volume as the capacity, or the amount of a liquid or substance, it can hold.
Unlike prisms, unit cubes do not fit nicely into a cylinder.
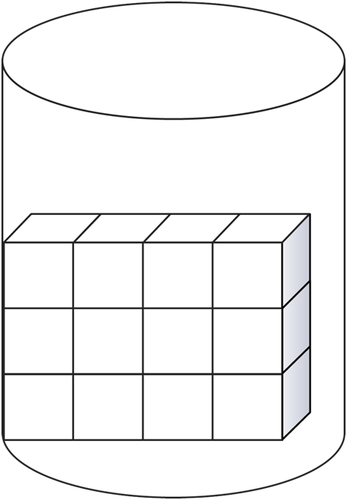
So, to calculate the volume of a cylinder accurately, you need to use a formula instead of unit cubes.
To calculate the volume of a cylinder, start by calculating the area of the circular base. That will give you a measure for the number of unit cubes that can fit across the bottom of the cylinder. The height of the cylinder will show how high cubes can be stacked inside the cylinder.
Here is the formula for finding the volume of a cylinder.
\(V&= \pi r^{2}h\)
Let’s apply this formula.
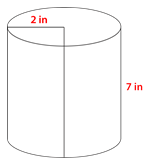
The radius of the circular base is 2 inches. The height of the cylinder is 7 inches. If you take both of these given measures and substitute them into the formula, you can solve for the volume of the cylinder.
\(\begin{aligned} V&= \pi r^{2} h \\ V&= (3.14)(2^{2})(7) \\ V&= (3.14)(4)(7) \\ V&= (3.14)(28) \\ V&= 87.92\text{ in}^{3}\end{aligned}\)
The volume of the cylinder is \(87.92\text{ in}^{3}\).
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Ramona and her extra fruit preserve.
Ramona has two food storage containers, but isn’t sure which will hold the most. How can Raymond use these dimensions to figure out which will hold the most?
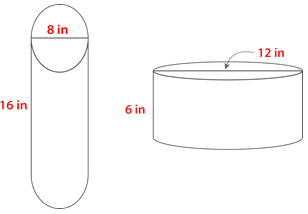
Solution
Start with the container on the left.
First, note that the diameter is twice the radius, so divide the diameter by 2 to get the radius.
8\divide 2=4
Radius is 4.
Next, substitute the given information into the formula then solve.
\(\begin{aligned}V&= \pi r^{2} h \\ V&= \pi (4)^{2} (16) \\ V&= \pi (16)(16) \\ V&= 256 \pi \\ V&= 803.84\text{ in}^{3}\end{aligned}\)
The first container holds 803.84 cubic inches.
Next, consider the other container.
First, note that the diameter is twice the radius, so divide the diameter by 2 to get the radius.
12\divide 2=6
Radius is 6.
Next, substitute the given information into the formula then solve.
\(\begin{aligned}V&= \pi r^{2} h \\ V&= \pi (6)^{2} (6) \\ V&= \pi (36)(6) \\ V&= 216 \pi \\ V&= 678.24\text{ in}^{3}\end{aligned}\)
The second container holds 678.24 cubic inches.
The container on the left has the greatest volume.
Example \(\PageIndex{2}\)
Use the formula for finding the volume of a cylinder to answer the following question.
A water tank has a radius of 50 feet and a height of 400 feet. How many cubic feet of water will the tank hold when it is full?
Solution
First, substitute the given information into the formula and solve.
\(\begin{aligned}V&= \pi r^{2}h \\ V&= \pi (502)(400) \\ V&= \pi (2,500)(400) \\ V&= 1,000,000 \pi \\ V&= 3,140,000\text{ in}^{3}\end{aligned}\)
The water tank will hold more than 3 million cubic feet of water!
Example \(\PageIndex{3}\)
Find the volume of the cylinder.
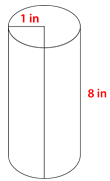
Solution
First, substitute the given information into the formula then solve.
\(\begin{aligned}V&= \pi r^{2} h \\ V&= \pi (1^{2})(8) \\ V&= \pi (1)(8) \\ V&= 8 \pi \\ V&= 25.12\text{ in}^{3}\end{aligned}\)
The answer is 25.12 cubic inches.
Example \(\PageIndex{4}\)
Find the volume of the cylinder.
d=10 \text{ ft}\), \(h=12 \text{ ft}\)
Solution
First, note that the diameter is twice the radius, so divide the diameter by 2 to get the radius.
10\divide 2=5\)
Radius is 5.
Next, substitute the given information into the formula then solve.
\(\begin{aligned}V&= \pi r^{2} h \\ V&= \pi (5)^{2} (12) \\ V&= \pi (25)(12) \\ V&= 300 \pi \\ V&= 942 \text{ ft}^{3}\end{aligned}\)
The answer is 942 cubic feet.
Example \(\PageIndex{5}\)
Find the volume of the cylinder.
\(r=6\text{ in}\), \(h=10\text{ in}\)
Solution
First, substitute the given information into the formula then solve.
\(\begin{aligned}V&= \pi r^{2} h \\ V&= \pi (6)^{2}(10) \\ V&= \pi (36)(10) \\ V&= 360 \pi \\ V&= 1130.4\text{ in}^{3}\end{aligned}\)
The answer is 1130.4 cubic inches.
Review
Find the volume of each of the following cylinders.
- \(r=5\text{ in}\), \(h=8\text{ in}\)
- \(r=4\text{ in}\), \(h=7\text{ in}\)
- \(r=3 \text{ ft}\), \(h=5 \text{ ft}\)
- \(r=3 \text{ ft}\), \(h=8 \text{ ft}\)
- \(r=4 \text{ cm}\), \(h=9 \text{ cm}\)
-
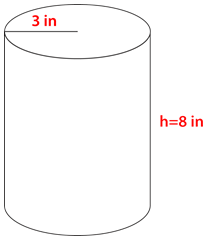
Figure \(\PageIndex{7}\) -
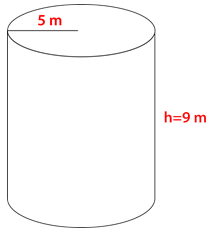
Figure \(\PageIndex{8}\) -
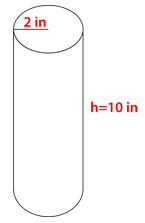
Figure \(\PageIndex{9}\) -
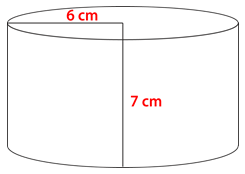
Figure \(\PageIndex{10}\) -
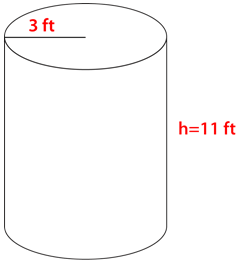
Figure \(\PageIndex{11}\) -
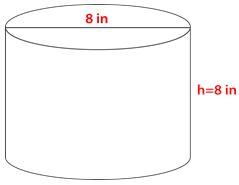
Figure \(\PageIndex{12}\) -
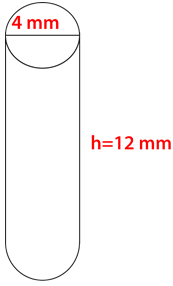
Figure \(\PageIndex{13}\) -
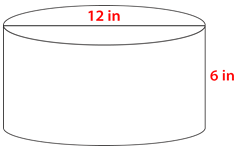
Figure \(\PageIndex{14}\) -
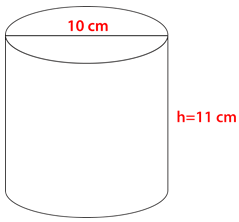
Figure \(\PageIndex{15}\) -
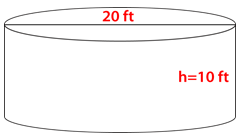
Figure \(\PageIndex{16}\)
Vocabulary
| Term | Definition |
|---|---|
| Cylinder | A cylinder is a solid figure with two parallel congruent circular bases. |
| Radius | The radius of a circle is the distance from the center of the circle to the edge of the circle. |
| Surface Area | Surface area is the total area of all of the surfaces of a three-dimensional object. |
| Volume | Volume is the amount of space inside the bounds of a three-dimensional object. |
Additional Resources
Interactive Element
Video: Solid Geometry Volume
Practice: Volume of Cylinders
Real World: Why Do Supertankers Float?