2.3.4: Coterminal Angles

Last updated
Save as PDF

Page ID: 14353

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Set of angles with the same terminal or end side.

While playing a game with friends, you use a spinner that looks like this:

f-d_f7240c6d67dc4c11a91ef52a9bd37ee4fffeff6e8b3f1b75cad23ab6+IMAGE_TINY+IMAGE_TINY.jpg — Figure \(\PageIndex{1}\)

As you can see, the angle that the spinner makes with the horizontal is \(60^{\circ}\). Is it possible to represent the angle any other way?

Coterminal Angles

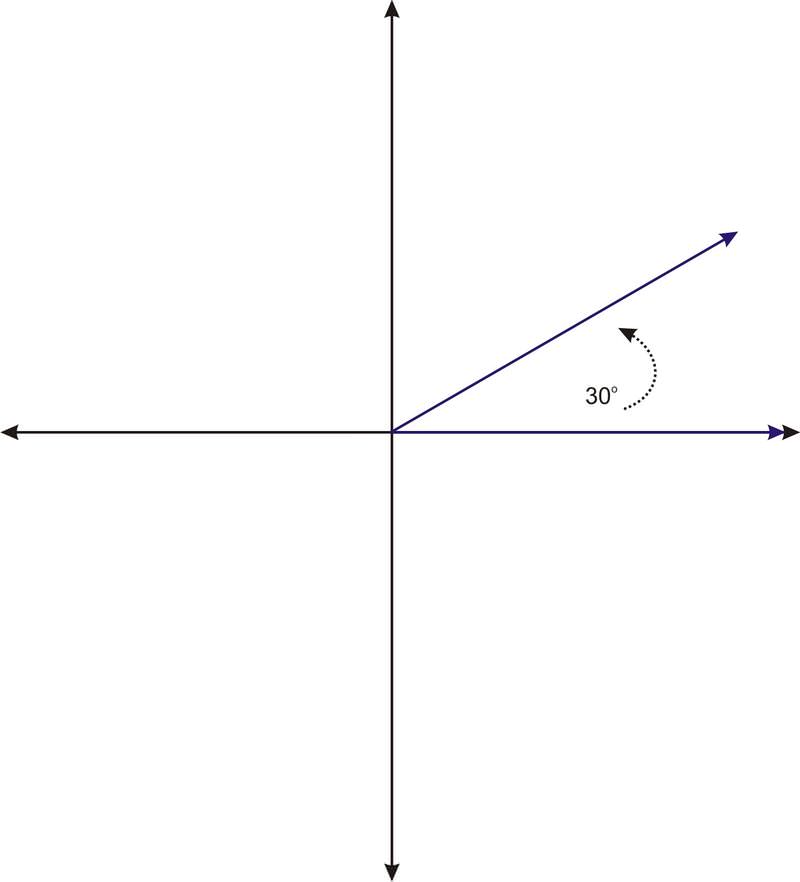
Consider the angle \(30^{\circ}\), in standard position.

f-d_bf84fee1daaa9b351764625d762ccde992c539f0991bc0c27057a764+IMAGE_TINY+IMAGE_TINY.jpg — Figure \(\PageIndex{2}\)

Now consider the angle \(390^{\circ}\). We can think of this angle as a full rotation (\(360^{\circ}\)), plus an additional 30 degrees.

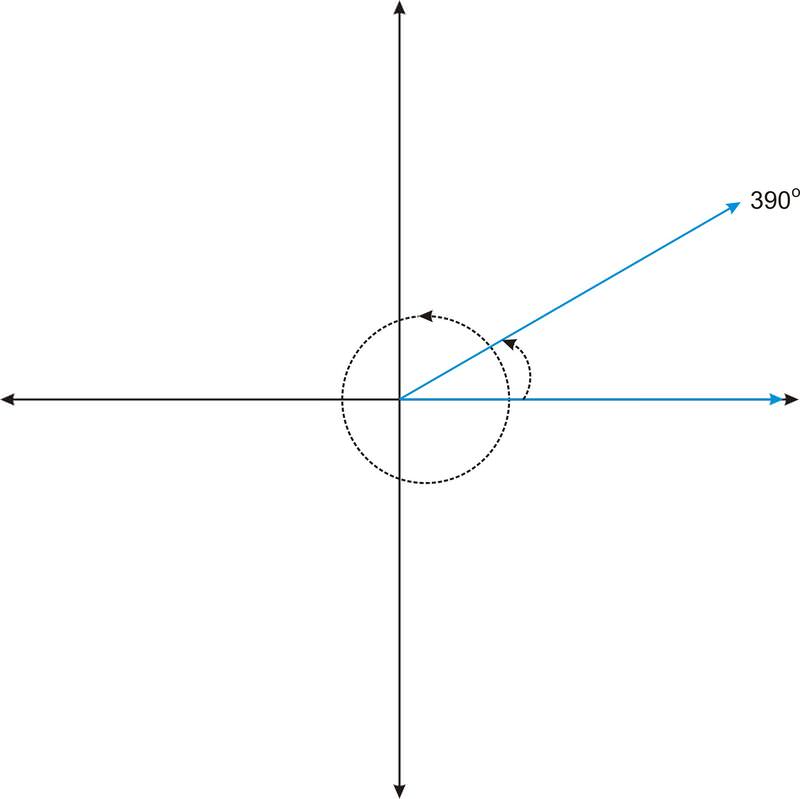
f-d_1d389b6f5ea40c5442bde599b63f42ab1653590f787828e2395c5057+IMAGE_TINY+IMAGE_TINY.jpg — Figure \(\PageIndex{3}\)

Notice that \(390^{\circ}\) looks the same as \(30^{\circ}\). Formally, we say that the angles share the same terminal side. Therefore we call the angles co-terminal. Not only are these two angles co-terminal, but there are infinitely many angles that are co-terminal with these two angles. For example, if we rotate another \(360^{\circ}\), we get the angle \(750^{\circ}\). Or, if we create the angle in the negative direction (clockwise), we get the angle \(−330^{\circ}\). Because we can rotate in either direction, and we can rotate as many times as we want, we can continuously generate angles that are co-terminal with \(30^{\circ}\).

Identifying Co-Terminal Angles

For the following questions, determine if the angle is co-terminal with \(45^{\circ}\).

1. \(−45^{\circ}\)

No, it is not co-terminal with \(45^{\circ}\)

2. \(405^{\circ}\)

Yes, \(405^{\circ}\) is co-terminal with \(45^{\circ}\).

3. \(−315^{\circ}\)

Yes, \(−315^{\circ}\) is co-terminal with \(45^{\circ}\).

Example \(\PageIndex{1}\)

Earlier, you were asked if it is possible to represent the angle any other way.

Solution

You can either think of \(60^{\circ}\) as \(420^{\circ}\) if you rotate all the way around the circle once and continue the rotation to where the spinner has stopped, or as \(−300^{\circ}\) if you rotate clockwise around the circle instead of counterclockwise to where the spinner has stopped.

Example \(\PageIndex{2}\)

Find a coterminal angle to \(23^{\circ}\)

Solution

A coterminal angle would be an angle that is at the same terminal place as \(23^{\circ}\) but has a different value. In this case, \(−337^{\circ}\) is a coterminal angle.

Example \(\PageIndex{3}\)

Find a coterminal angle to \(−90^{\circ}\)

Solution

A coterminal angle would be an angle that is at the same terminal place as −90^{\circ}\) but has a different value. In this case, \(270^{\circ}\) is a coterminal angle.

Example \(\PageIndex{4}\)

Find two coterminal angles to \(70^{\circ}\) by rotating in the positive direction around the circle.

Solution

Rotating once around the circle gives a coterminal angle of \(430^{\circ}\). Rotating again around the circle gives a coterminal angle of \(790^{\circ}\).

Review

Is \(315^{\circ}\) co-terminal with \(−45^{\circ}\)?
Is \(90^{\circ}\) co-terminal with \(−90^{\circ}\)?
Is \(350^{\circ}\) co-terminal with \(−370^{\circ}\)?
Is \(15^{\circ}\) co-terminal with \(1095^{\circ}\)?
Is \(85^{\circ}\) co-terminal with \(1880^{\circ}\)?

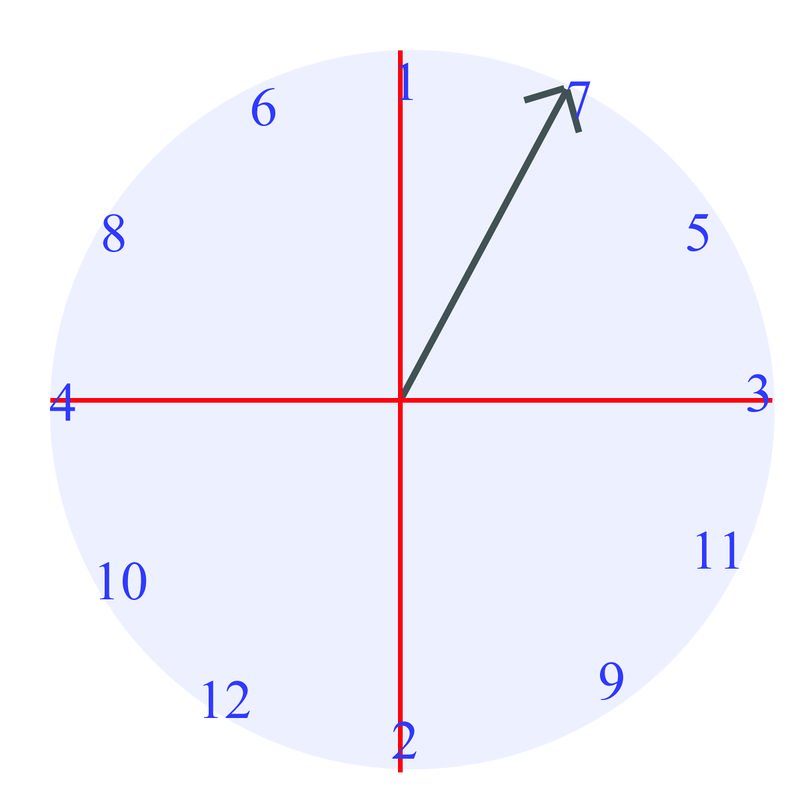
For each diagram, name the angle in 3 ways. At least one way should use negative degrees.

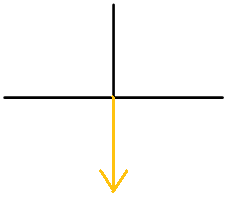
Figure \(\PageIndex{4}\)
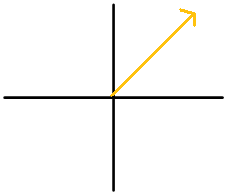
Figure \(\PageIndex{5}\)
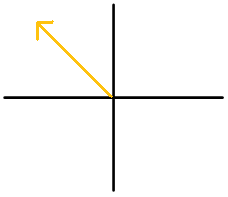
Figure \(\PageIndex{6}\)
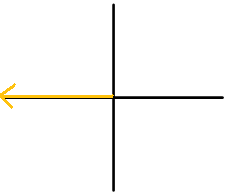
Figure \(\PageIndex{7}\)
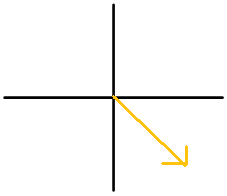
Figure \(\PageIndex{8}\)
Name the angle of the 8 on a standard clock two different ways.
Name the angle of the 11 on a standard clock two different ways.
Name the angle of the 4 on a standard clock two different ways.
Explain how to determine whether or not two angles are co-terminal.
How many rotations is \(4680^{\circ}\)?

Review (Answers)

To see the Review answers, open this PDF file and look for section 1.16.

Vocabulary

Term	Definition
Coterminal Angles	A set of coterminal angles are angles with the same terminal side but expressed differently, such as a different number of complete rotations around the unit circle or angles being expressed as positive versus negative angle measurements.

Additional Resources

Interactive Element

Video: Example: Determine if Two Angles are Coterminal

Practice: Coterminal Angles