2.3.5: Signs of Trigonometric Functions
- Page ID
- 14454
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)\(x\) and \(y\) values of a function; signs of functions based on quadrants.
Domain, Range, and Signs of Trigonometric Functions
You are doodling in art class one day when you draw a circle. Then you draw a few lines extending outward from the center to the edge of the circle. You draw a triangle with the "\(x\)" axis, and realize that you're thinking about your math class again.
You notice that the relationship for the sine function involves the length of the side opposite the angle divided by the length of the hypotenuse. But while the hypotenuse is always a positive number, the sign of the opposite side can be different, depending on what quadrant the angle is drawn in.
Can you determine what the sign of the sine function will be in each of the four quadrants, based on the knowledge of the ratio that defines the sine function?
Domain and Range of Trigonometric Functions
While the trigonometric functions may seem quite different from other functions you have worked with, they are in fact just like any other function. We can think of a trig function in terms of “input” and “output.” The input is always an angle. The output is a ratio of sides of a triangle. If you think about the trig functions in this way, you can define the domain and range of each function.
Let’s first consider the sine and cosine functions. The input of each of these functions is always an angle, and as you learned in the previous sections, these angles can take on any real number value. Therefore the sine and cosine function have the same domain, the set of all real numbers, \(R\). We can determine the range of the functions if we think about the fact that the sine of an angle is the \(y\)−coordinate of the point where the terminal side of the angle intersects the unit circle. The cosine is the \(x\)−coordinate of that point. Now recall that in the unit circle, we defined the trig functions in terms of a triangle with hypotenuse 1.
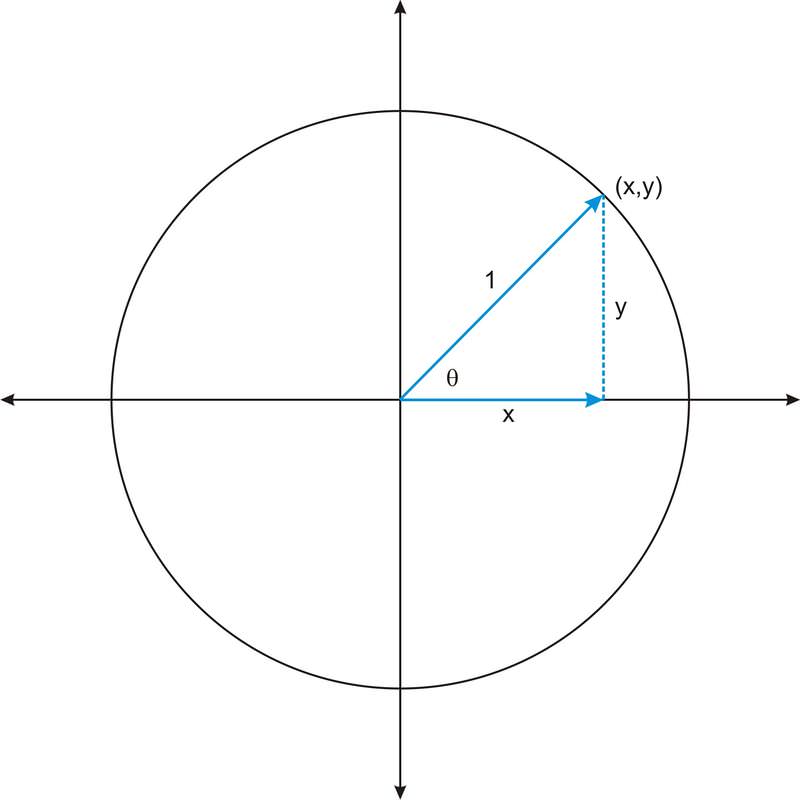
In this right triangle, \(x\) and \(y\) are the lengths of the legs of the triangle, which must have lengths less than 1, the length of the hypotenuse. Therefore the ranges of the sine and cosine function do not include values greater than one. The ranges do, however, contain negative values. Any angle whose terminal side is in the third or fourth quadrant will have a negative \(y\)−coordinate, and any angle whose terminal side is in the second or third quadrant will have a negative \(x\)−coordinate.
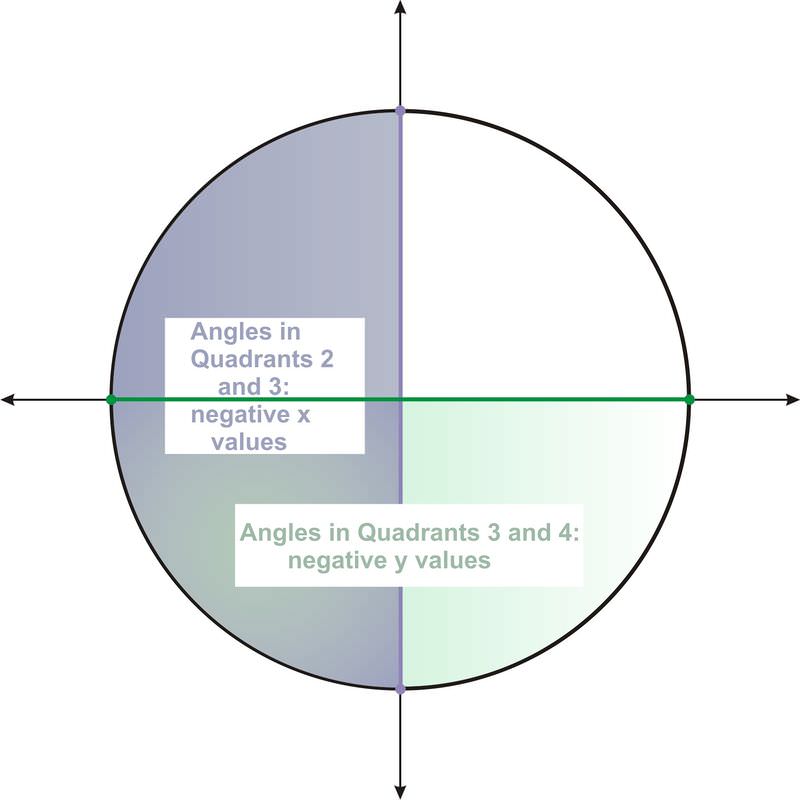
In either case, the minimum value is -1. For example, \(\cos 180^{\circ} =−1\) and \(\sin 270^{\circ} =−1\). Therefore the sine and cosine function both have range from -1 to 1.
The table below summarizes the domains and ranges of these functions:
| Domain | Range | |
|---|---|---|
| Sine | \(\theta =R\) | \(−1\leq y\leq 1\) |
| Cosine | \(\theta =R\) | \(−1\leq y\leq 1\) |
Knowing the domain and range of the cosine and sine function can help us determine the domain and range of the secant and cosecant function. First consider the sine and cosecant functions, which as we showed above, are reciprocals. The cosecant function will be defined as long as the sine value is not 0. Therefore the domain of the cosecant function excludes all angles with sine value 0, which are \(0^{\circ}\), \(180^{\circ}\), \(360^{\circ}\), etc.
In Chapter 2 you will analyze the graphs of these functions, which will help you see why the reciprocal relationship results in a particular range for the cosecant function. Here we will state this range, and in the review questions you will explore values of the sine and cosecant function in order to begin to verify this range, as well as the domain and range of the secant function.
| Function | Domain | Range |
|---|---|---|
| Tangent | \(\theta \in R,\theta \neq 90,270,450 \ldots\) | All reals |
| Cotangent | \(\theta \in R,\theta \neq 0,180,360 \ldots\) | All reals |
Now let’s consider the tangent and cotangent functions. The tangent function is defined as \(\tan \theta =\dfrac{y}{x}\). Therefore the domain of this function excludes angles for which the ordered pair has an \(x\)−coordinate of 0: \(90^{\circ}\), \(270^{\circ}\), etc. The cotangent function is defined as \(\cot \theta =\dfrac{x}{y}\), so this function’s domain will exclude angles for which the ordered pair has a \(y\)−coordinate of 0: \(0^{\circ} \), \(180^{\circ}\), \(360^{\circ}\), etc.
| Function | Domain | Range |
|---|---|---|
| Tangent | \(\theta \in R, \theta \neq 90,270,450\ldots\) | All reals |
| Cotangent | \(\theta \in R,\theta \neq 0 ,180 ,360 \ldots\) | All reals |
Knowing the ranges of these functions tells you the values you should expect when you determine the value of a trig function of an angle. However, for many problems you will need to identify the sign of the function of an angle: Is it positive or negative?
In determining the ranges of the sine and cosine functions above, we began to categorize the signs of these functions in terms of the quadrants in which angles lie. The figure below summarizes the signs for angles in all 4 quadrants.
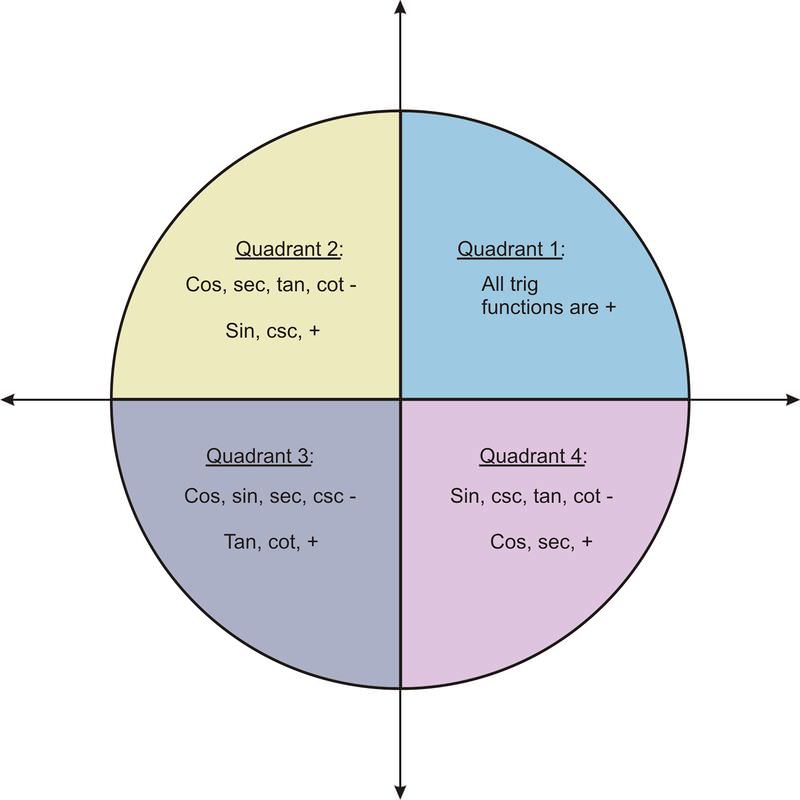
An easy way to remember this is “All Students Take Calculus”. Quadrant I: All values are positive, Quadrant II: Sine is positive, Quadrant III: Tangent is positive, and Quadrant IV: Cosine is positive. This simple memory device will help you remember which trig functions are positive and where.
Stating the Sign
1. State the sign of \(\cos 100^{\circ}\)
The angle \(100^{\circ}\) is in the second quadrant. Therefore the \(x\)−coordinate is negative and so \(\cos 100^{\circ}\) is negative.
2. State the sign of \(\csc 220^{\circ}\)
The angle \(220^{\circ}\) is in the third quadrant. Therefore the \(y\)−coordinate is negative. So the sine, and the cosecant are negative.
3. State the sign of \(\tan 370^{\circ}\)
The angle \(370^{\circ}\) is in the first quadrant. Therefore the tangent value is positive.
Earlier, you were asked to determine what the sign of the sine function will be in each of the four quadrants.
Solution
Since the sine function is defined to be the length of the opposite side divided by the length of the hypotenuse, the sign of the sine function is the sign of the y -coordinate for whatever quadrant is being considered. In quadrants 1 and 2, the "y" coordinate is positive, so the sine function is positive. In quadrants 3 and 4, the y-coordinate is negative, so the sine function is negative as well.
State the sign of \(\cos 70^{\circ}\)
Solution
The angle \(70^{\circ}\) is in the first quadrant. Cosine is defined to be the adjacent side divided by the hypotenuse. Since the hypotenuse of the unit circle is one and the adjacent side is the \(x\)-coordinate, the sign of the cosine function is determined by the sign of the \(x\)-coordinate. Since \(70^{\circ}\) is in the first quadrant, the \(x\) value is positive. Therefore the cosine value is positive.
State the sign of \(\sin 130^{\circ}\)
Solution
The angle \(130^{\circ}\) is in the second quadrant. Sine is defined to be the opposite side divided by the hypotenuse. Since the hypotenuse of the unit circle is one and the opposite side is the y-coordinate, the sign of the sine function is determined by the sign of the \(y\)-coordinate. Since \(130^{\circ}\) is in the second quadrant, the \(y\) value is positive. Therefore the sine value is positive.
State the sign of \(\tan 250^{\circ}\)
Solution
The angle \(250^{\circ}\) is in the third quadrant. Tangent is defined to be the opposite side divided by the adjacent side. In the third quadrant, the \(x\) values are negative, and the y values are negative. A negative divided by a negative equals a positive. Therefore the tangent of \(250^{\circ}\) is positive.
Review
- In what quadrants is the sine function positive?
- In what quadrants is the cotangent function negative?
- In what quadrants is the cosine function negative?
- In what quadrants is the tangent function positive?
- For what angles is the cosecant function undefined?
- State the sign of \(\sin 510^{\circ} \).
- State the sign of \(\cos 315^{\circ} \).
- State the sign of \(\tan 135^{\circ} \).
- State the sign of \(\cot 220^{\circ} \).
- State the sign of \(\csc 40^{\circ} \).
- State the sign of \(\cos 330^{\circ} \).
- State the sign of \(\sin 60^{\circ} \).
- State the sign of \(\sec −45^{\circ} \).
- Explain why the cosecant function is never equal to 0.
- Using your knowledge of domain and range, make a possible sketch for \(y= \sin x\).
Review (Answers)
To see the Review answers, open this PDF file and look for section 1.22.
Vocabulary
| Term | Definition |
|---|---|
| domain | The domain of a function is the set of \(x\)-values for which the function is defined. |
| Range | The range of a function is the set of \(y\)-values for which the function is defined. |
Additional Resources
Video: Domain, Range, and Signs of Trigonometric Functions
Practice: Signs of Trigonometric Functions

