2.3.6: Trigonometric Functions and Angles of Rotation
- Page ID
- 14455
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Based on the unit circle.
You've been working hard in your math class, and are getting to be quite the expert on trig functions. Then one day your friend, who is a year ahead of you in school, approaches you.
"So, you're doing pretty well in math? And you're good with trig functions?" he asks with a smile.
"Yes," you reply confidently. "I am."
"Alright, then what's the sine of \(150^{\circ}\)?" he asks.
"What? That doesn't make sense. No right triangle has an angle like that, so there's no way to define that function!" you say.
Your friend laughs. "As it turns out, it is quite possible to have trig functions of angles greater than \(90^{\circ}\)."
Is your friend just playing a joke on you, or does he mean it? Can you actually calculate \(\sin 150^{\circ}\)?
Angles of Rotation and Trigonometric Functions
Just as it is possible to define the six trigonometric functions for angles in right triangles, we can also define the same functions in terms of angles of rotation.
Consider an angle in standard position, whose terminal side intersects a circle of radius \(r\). We can think of the radius as the hypotenuse of a right triangle:
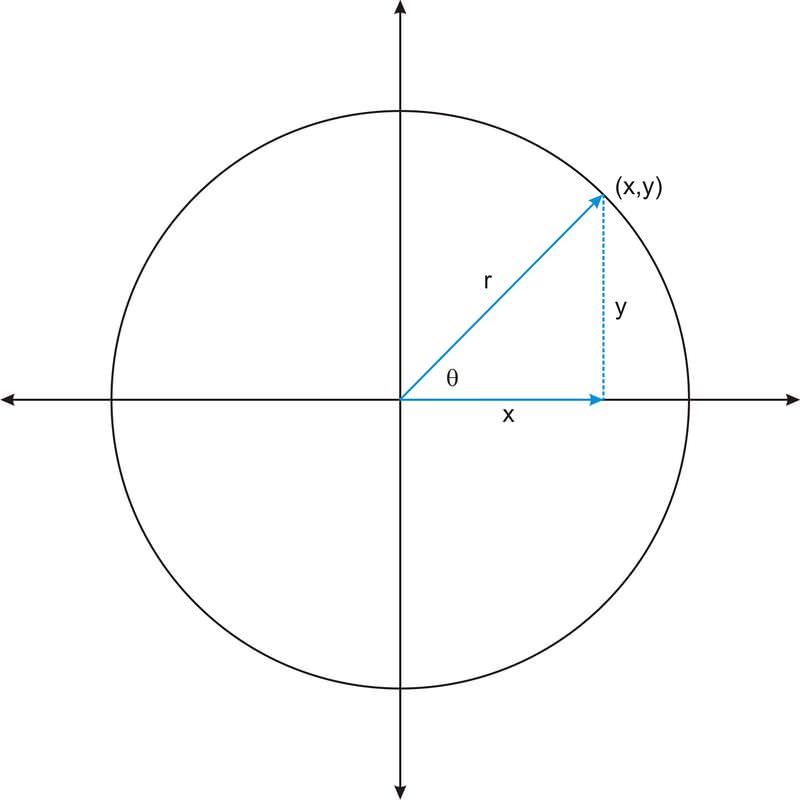
The point \((x,y)\) where the terminal side of the angle intersects the circle tells us the lengths of the two legs of the triangle. Now, we can define the trigonometric functions in terms of \(x\), \(y\), and \(r\):
\(\begin{aligned}
\cos \theta &=\dfrac{x}{r} & & \sec \theta=\dfrac{r}{x} \\
\sin \theta &=\dfrac{y}{r} & & \csc \theta=\dfrac{r}{y} \\
\tan \theta &=\dfrac{y}{x} & & \cot \theta=\dfrac{x}{y}
\end{aligned}\)
And, we can extend these functions to include non-acute angles.
Consider an angle in standard position, such that the point \((x,y)\) on the terminal side of the angle is a point on a circle with radius 1.
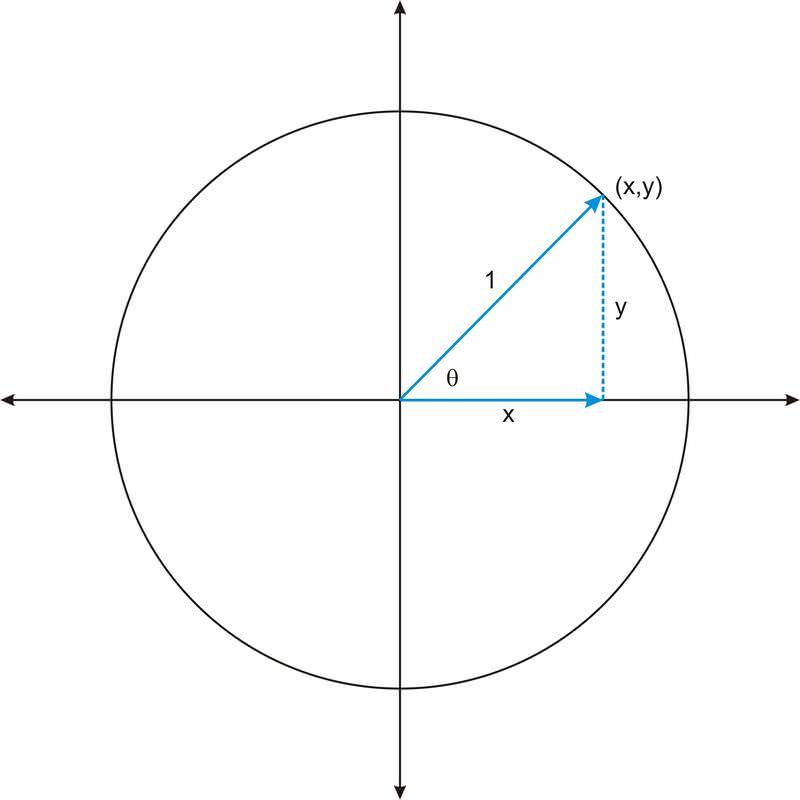
This circle is called the unit circle. With \(r=1\), we can define the trigonometric functions in the unit circle:
\(\begin{array}{lll}
\cos \theta=\dfrac{x}{r}=\dfrac{x}{1}=x & & \sec \theta=\dfrac{r}{x}=\dfrac{1}{x} \\
\sin \theta=\dfrac{y}{r}=\dfrac{y}{1}=y & & \csc \theta=\dfrac{r}{y}=\dfrac{1}{y} \\
\tan \theta=\dfrac{y}{x} & & \cot \theta=\dfrac{x}{y}
\end{array}\)
Notice that in the unit circle, the sine and cosine of an angle are the \(y\) and \(x\) coordinates of the point on the terminal side of the angle. Now we can find the values of the trigonometric functions of any angle of rotation, even the quadrantal angles, which are not angles in triangles.
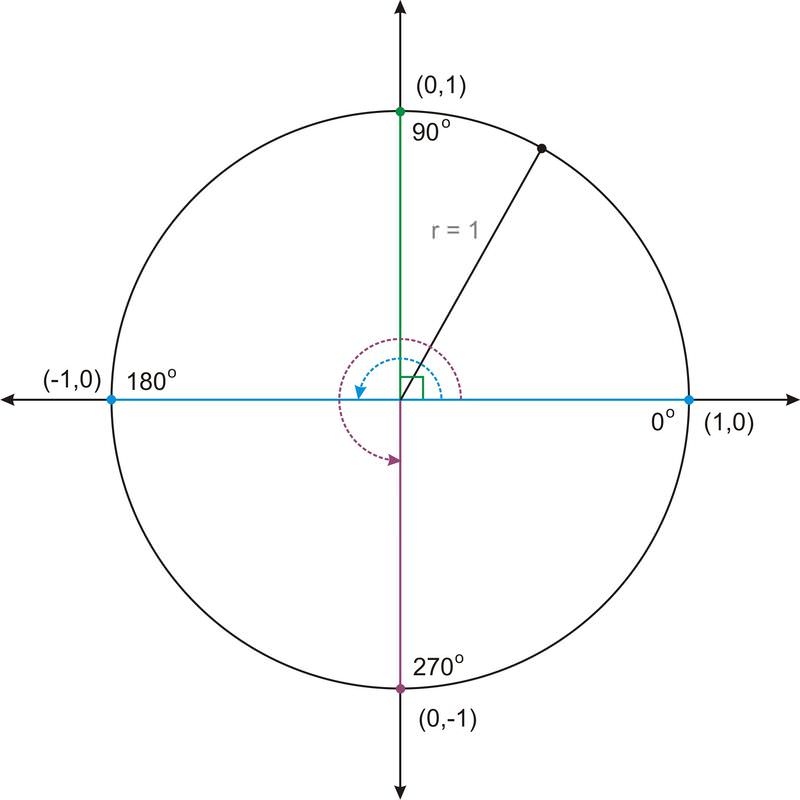
We can use the figure above to determine values of the trig functions for the quadrantal angles. For example, \(\sin 90^{\circ}=y=1\).
Determining the Value of Trigonometric Functions
1. Determine the values of the six trigonometric functions.
The point \((-3, 4)\) is a point on the terminal side of an angle in standard position. Determine the values of the six trigonometric functions of the angle.
Notice that the angle is more than 90 degrees, and that the terminal side of the angle lies in the second quadrant. This will influence the signs of the trigonometric functions.
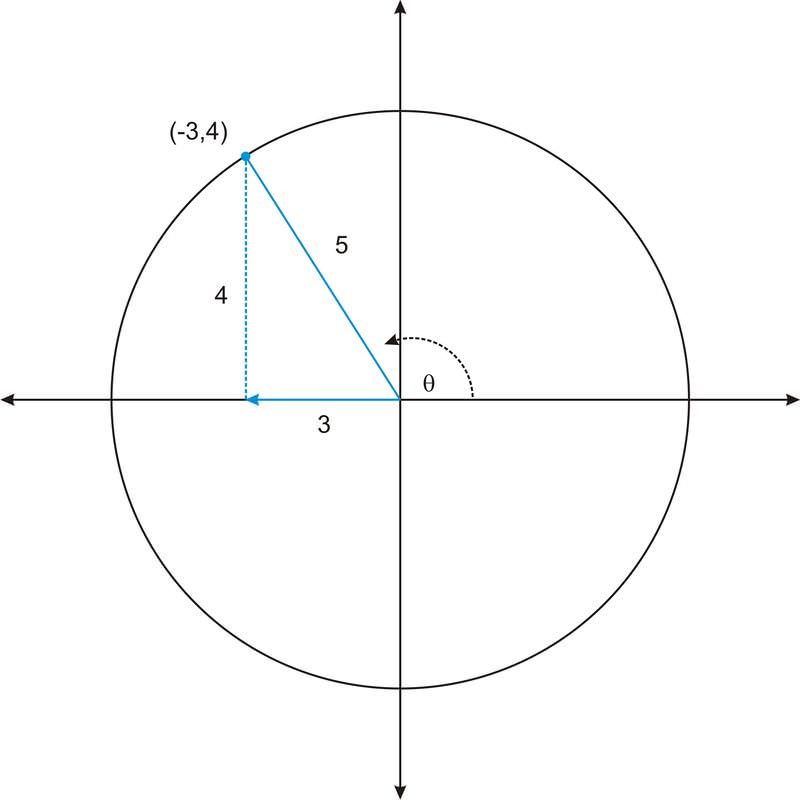
\(\begin{aligned}
\cos \theta &=\dfrac{-3}{5} & & \sec \theta=\dfrac{5}{-3} \\
\sin \theta &=\dfrac{4}{5} & & \csc \theta=\dfrac{5}{4} \\
\tan \theta &=\dfrac{4}{-3} & & \cot \theta=\dfrac{-3}{4}
\end{aligned}\)
Notice that the value of \(r\) depends on the coordinates of the given point. You can always find the value of \(r\) using the Pythagorean Theorem. However, often we look at angles in a circle with radius 1. As you can see, doing this allows us to simplify the definitions of the trig functions.
2. Use the unit circle above to find the value of \(\cos 90^{\circ}\)
\(\cos 90^{\circ}=0\)
The ordered pair for this angle is (0, 1). The cosine value is the \(x\) coordinate, .
3. Use the unit circle above to find the value of \(\cot 180^{\circ}\)
\(\cot 180^{\circ}\) is undefined
The ordered pair for this angle is (-1, 0). The ratio \(\dfrac{x}{y}\) is \(\dfrac{−1}{0}\), which is undefined.
Earlier, you were asked if you can actually calculate \(\sin 150^{\circ}\).
Solution
Since you now know that it is possible to apply trigonometric functions to angles greater than \(90^{\circ}\), you can calculate the \(\sin 150^{\circ}\). The easiest way to do this without difficulty is to consider that an angle of \(150^{\circ}\) is in the same position as \(30^{\circ}\), except it's in the second quadrant. This means that it has the same "\(x\)" and "\(y\)" values as \(30^{\circ}\), except that the "x" value is negative.
Therefore,
\(\sin 150^{\circ}=\dfrac{1}{2}\)
Use this figure:
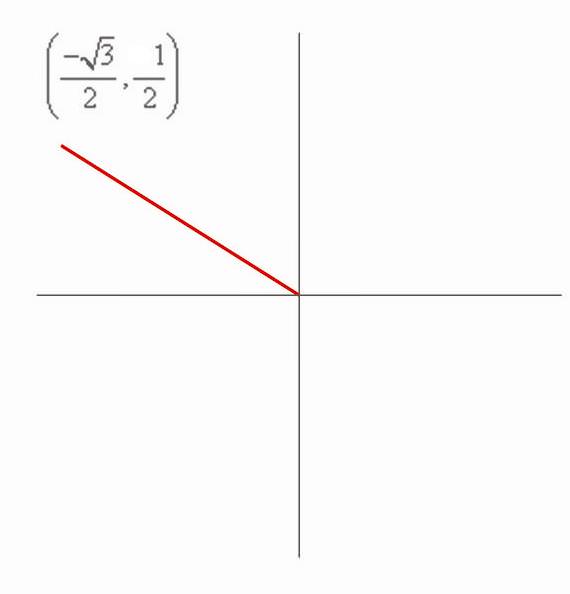
to answer the following examples.
Find \(\cos \theta\) on the circle above.
Solution
We can see from the "\(x\)" and "\(y\)" axes that the "\(x\)" coordinate is \(−\dfrac{\sqrt{3}}{2}\), the "\(y\)" coordinate is \(\dfrac{1}{2}\), and the hypotenuse has a length of 1. This means that the cosine function is:
\(\cos \theta=\dfrac{\text { adjacent }}{\text { hypotenuse }}=\dfrac{\dfrac{-\sqrt{3}}{2}}{1}=\dfrac{-\sqrt{3}}{2}\)
Find \(\cot \theta \) on the circle above.
Solution
We know that \(\cot =\dfrac{1}{\tan }=\dfrac{1}{\dfrac{\text { opposite }}{\text { adjacent }}}=\dfrac{\text { adjacent }}{\text { opposite }}\). The adjacent side to \theta in the circle is \(−\dfrac{\sqrt{3}}{2}\) and the opposite side is \(\dfrac{1}{2}\). Therefore,
\(\cot \theta=\dfrac{\dfrac{-\sqrt{3}}{2}}{\dfrac{1}{2}}=-\sqrt{3}\)
Find \(\csc\theta \) on the circle above.
Solution
We know that \(\csc =\dfrac{1}{\sin }=\dfrac{1}{\dfrac{\text { opposite }}{\text { hypotenuse }}}=\dfrac{\text { hypotenuse }}{\text { opposite }}\). The opposite side to \(\theta\) in the circle is \(\dfrac{1}{2}\) and the hypotenuse is 1. Therefore,
\(\csc \theta=\dfrac{\text { hypotenuse }}{\text { opposite }}=\dfrac{1}{\dfrac{1}{2}}=2\)
Review
Find the values of the six trigonometric functions for each angle below.
- \(0^{\circ}\)
- \(90^{\circ}\)
- \(180^{\circ}\)
- \(270^{\circ}\)
- Find the sine of an angle that goes through the point \(\left (\dfrac{\sqrt{2}}{2},\dfrac{\sqrt{2}}{2}\right)\).
- Find the cosine of an angle that goes through the point \(\left (\dfrac{\sqrt{2}}{2},\dfrac{\sqrt{2}}{2}\right)\).
- Find the tangent of an angle that goes through the point \(\left (\dfrac{\sqrt{2}}{2},\dfrac{\sqrt{2}}{2}\right)\).
- Find the secant of an angle that goes through the point \(\left (−\dfrac{\sqrt{3}}{2},\dfrac{1}{2}\right)\).
- Find the cotangent of an angle that goes through the point \(\left (−\dfrac{\sqrt{3}}{2},−\dfrac{1}{2}\right)\).
- Find the cosecant of an angle that goes through the point \(\left (\dfrac{\sqrt{3}}{2},\dfrac{1}{2}\right)\).
- Find the sine of an angle that goes through the point \(\left (\dfrac{1}{2},−\dfrac{\sqrt{3}}{2}\right)\).
- Find the cosine of an angle that goes through the point \(\left (−\dfrac{\sqrt{3}}{2}, \dfrac{1}{2}\right)\).
- The sine of an angle in the first quadrant is 0.25. What is the cosine of this angle?
- The cosine of an angle in the first quadrant is 0.8. What is the sine of this angle?
- The sine of an angle in the first quadrant is 0.15. What is the cosine of this angle?
Review (Answers)
To see the Review answers, open this PDF file and look for section 1.17.
Vocabulary
| Term | Definition |
|---|---|
| Quadrantal Angle | A quadrantal angle is an angle that has its terminal side on one of the four lines of axis: positive x, negative x, positive y or negative y. |

