2.3.7: Reference Angles and Angles in the Unit Circle
- Page ID
- 14458
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Formed between the terminal side of an angle and the closest part of the \(x\)-axis.
When you walk into math class one day, your teacher has a surprise for the class. You're going to play series of games related to the things you've been learning about in class. For the first game, your teacher hands each group of students a spinner with an "\(x\)" and "\(y\)" axis marked. The game is to see how many angles you identify correctly. However, in this game, you are supposed to give what is called the "reference angle". You spin your spinner three times. Each picture below shows one of the spins:
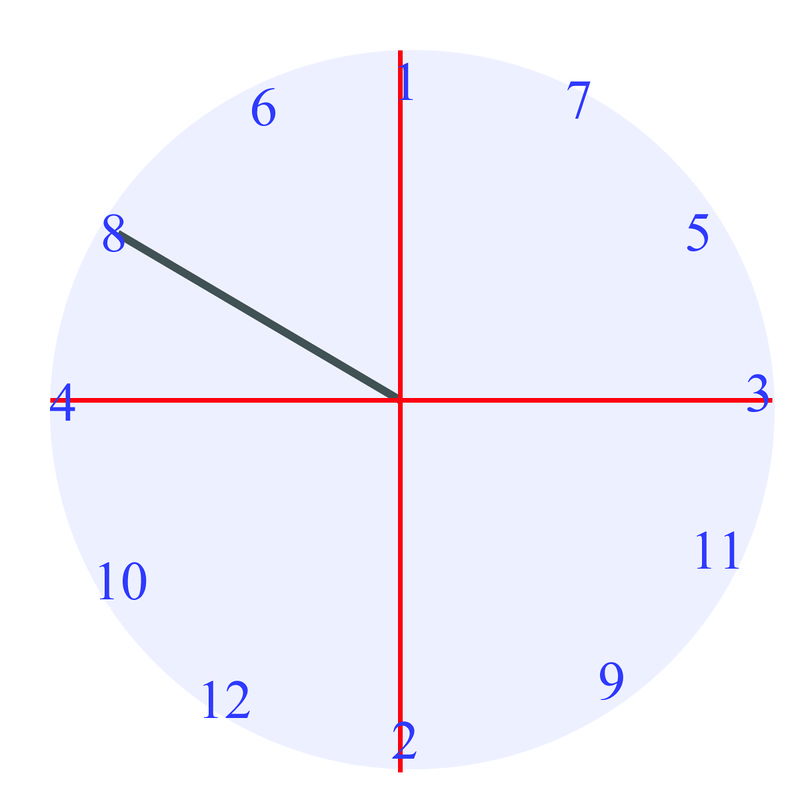
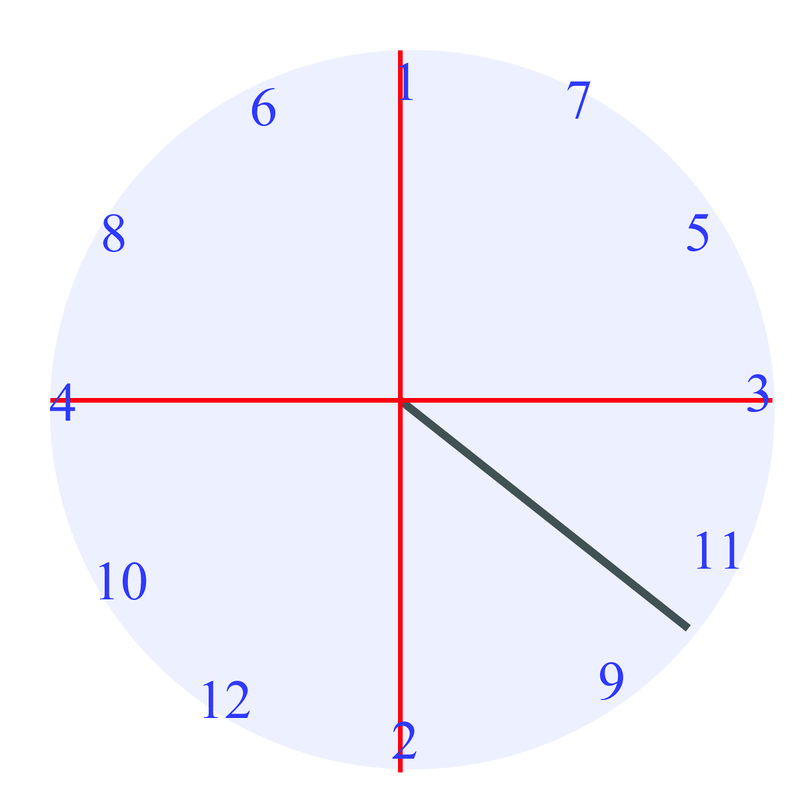
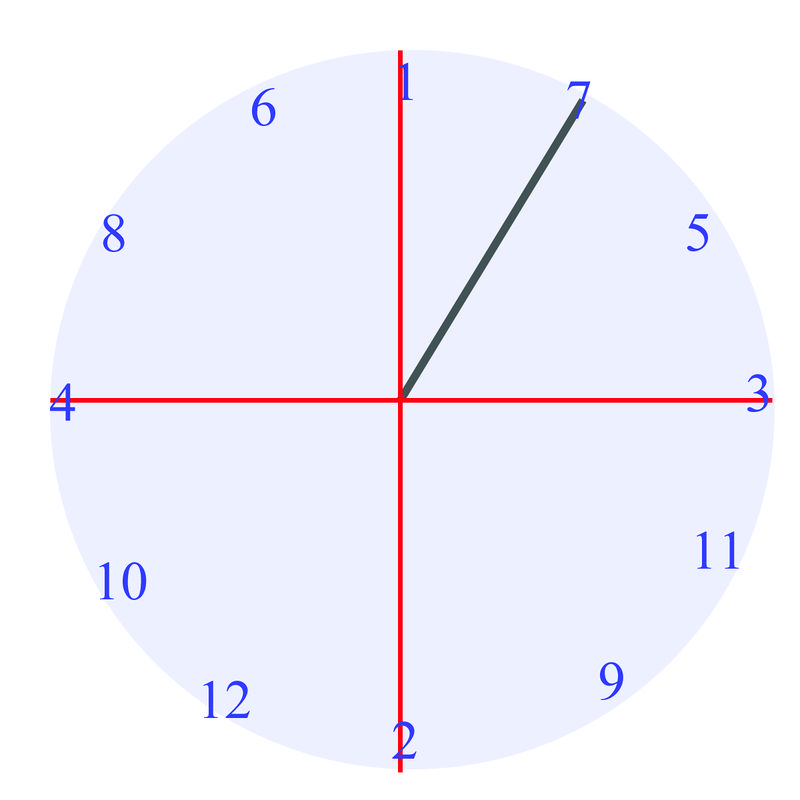
Can you correctly identify the reference angles for these pictures?
Reference Angles
Consider the angle \(150^{\circ}\). If we graph this angle in standard position, we see that the terminal side of this angle is a reflection of the terminal side of \(30^{\circ}\), across the \(y\)−axis.
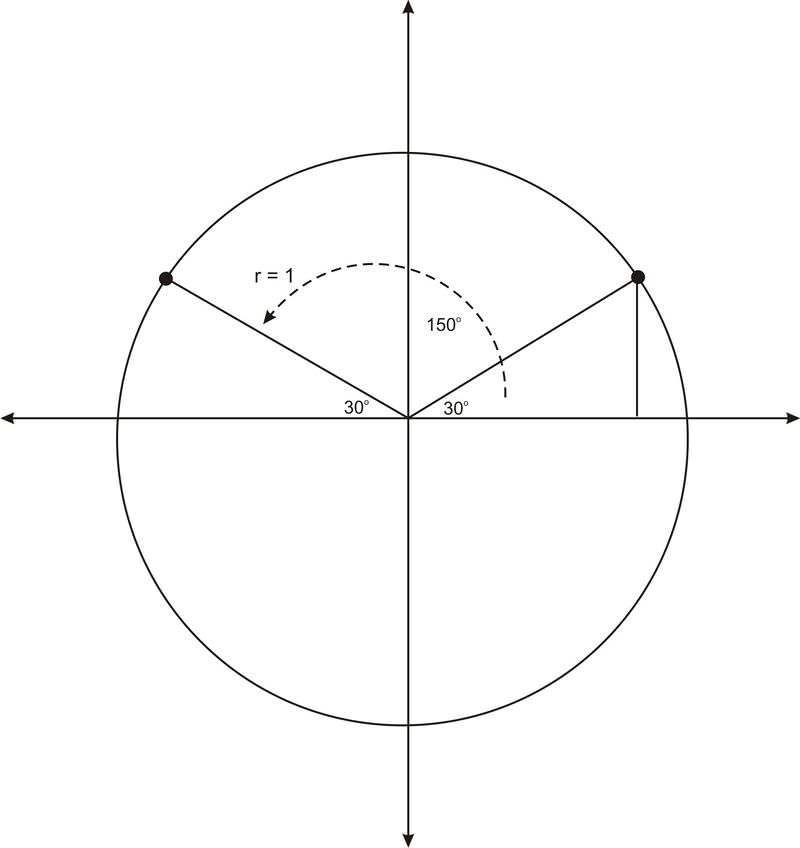
Notice that \(150^{\circ}\) makes a \(30^{\circ} \) angle with the negative \(x\)-axis. Therefore we say that \(30^{\circ}\) is the reference angle for \(150^{\circ}\). Formally, the reference angle of an angle in standard position is the angle formed with the closest portion of the \(x\)-axis. Notice that \(30^{\circ}\) is the reference angle for many angles. For example, it is the reference angle for \(210^{\circ}\) and for \(−30^{\circ}\).
In general, identifying the reference angle for an angle will help you determine the values of the trig functions of the angle.
Identifying Reference Angles
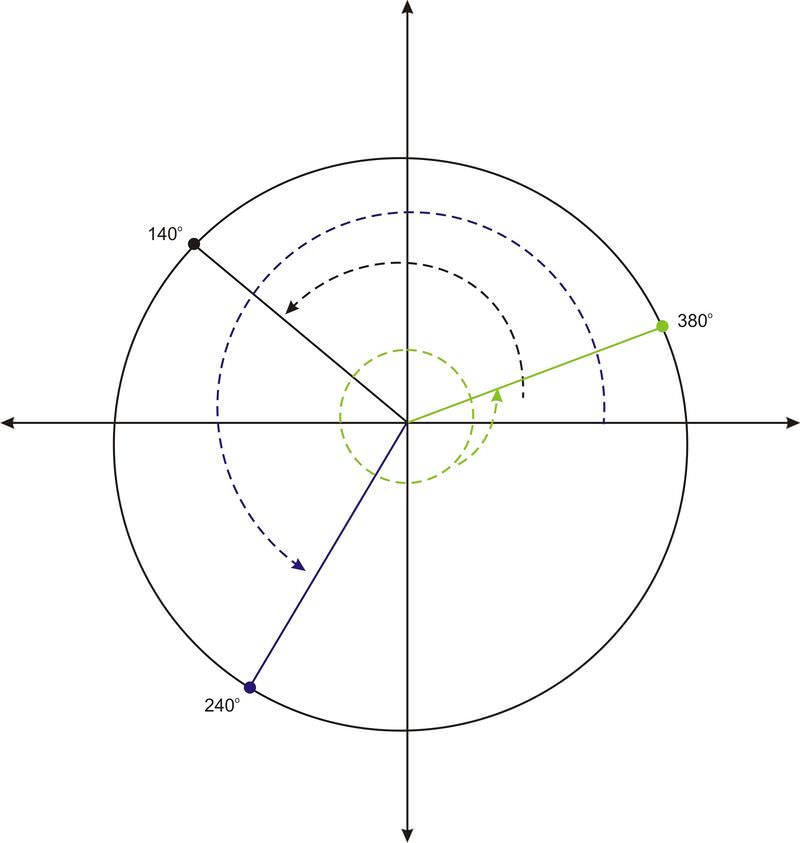
Graph each of the following angles and identify their reference angles.
a. \(140^{\circ}\)
\(140^{\circ} \) makes a \(40^{\circ} \) angles with the negative \(x\)-axis. Therefore the reference angle is \(40^{\circ} \).
b. \(240^{\circ}\)
\(240^{\circ}\) makes a \(60^{\circ}\) angle with the negative \(x\)-axis. Therefore the reference angle is \(60^{\circ}\)
c. \(380^{\circ}\)
\(380^{\circ} \) is a full rotation of \(360^{\circ}\), plus an additional \(20^{\circ}\). So this angle is co-terminal with \(20^{\circ}\), and \(20^{\circ}\) is its reference angle.
Determining the Value of Trigonometric Functions
1. Find the ordered pair for \(240^{\circ}\) and use it to find the value of \(\sin 240^{\circ}\).
\(\sin 240^{\circ} =−\dfrac{\sqrt{3}}{2}\)
As we found in part b under the question above, the reference angle for \(240^{\circ}\) is \(60^{\circ}\). The figure below shows \(60^{\circ}\) and the three other angles in the unit circle that have \(60^{\circ}\) as a reference angle.
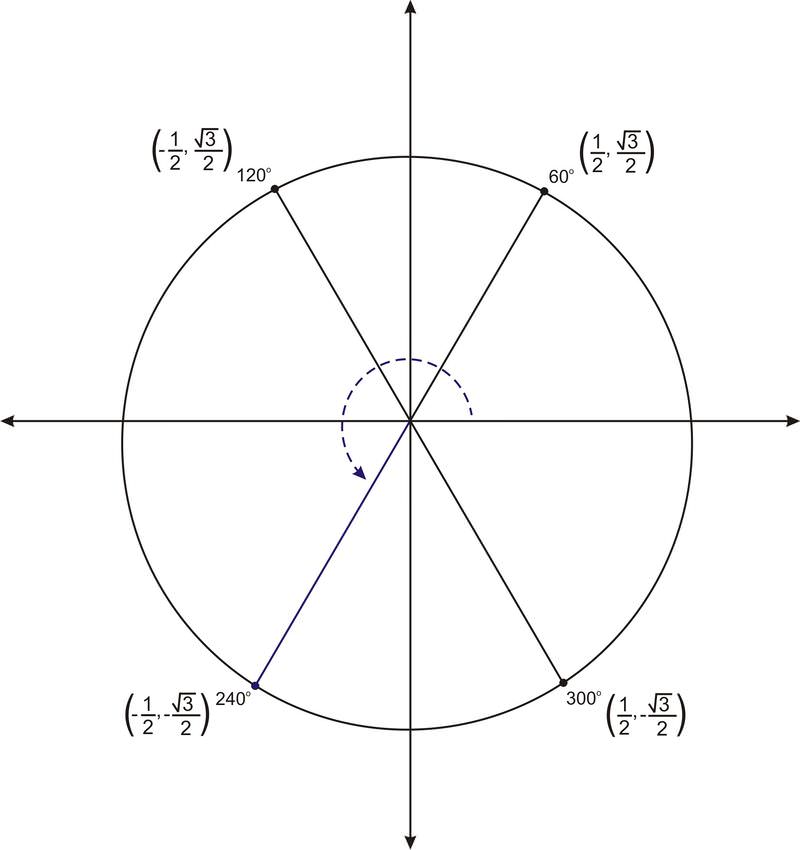
The terminal side of the angle \(240^{\circ}\) represents a reflection of the terminal side of \(60^{\circ}\) over both axes. So the coordinates of the point are \(\left(−\dfrac{1}{2},−\dfrac{\sqrt{3}}{2}\right)\). The y−coordinate is the sine value, so \(\sin 240^{\circ} =−\dfrac{\sqrt{3}}{2}\).
Just as the figure above shows \(60^{\circ}\) and three related angles, we can make similar graphs for \(30^{\circ}\) and \(45^{\circ}\).
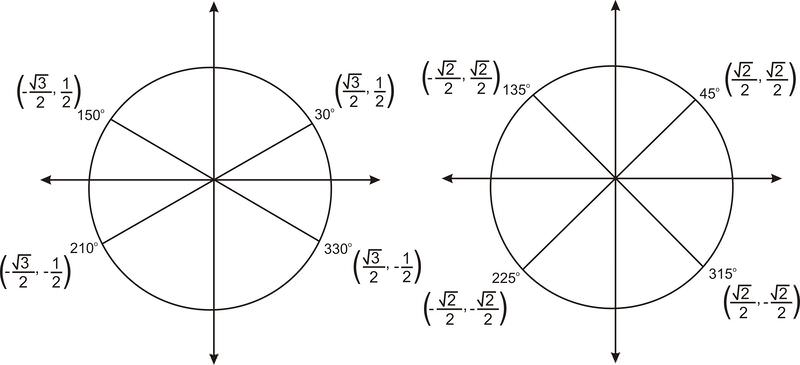
Knowing these ordered pairs will help you find the value of any of the trig functions for these angles.
2. Find the value of \(\cot 300^{\circ}\)
\(\cot 300^{\circ} =−\dfrac{1}{\sqrt{3}}\)
Using the graph above, you will find that the ordered pair is \(\left(\dfrac{1}{2},−\dfrac{\sqrt{3}}{2}\right)\). Therefore the cotangent value is \(\cot 300^{\circ}=\dfrac{x}{y}=\dfrac{\dfrac{1}{2}}{-\dfrac{\sqrt{3}}{2}}=\dfrac{1}{2} \times-\dfrac{2}{\sqrt{3}}=-\dfrac{1}{\sqrt{3}}\)
We can also use the concept of a reference angle and the ordered pairs we have identified to determine the values of the trig functions for other angles.
Earlier, you were asked if you can correctly identify the reference angles in the pictures.
Solution
Since you know how to measure reference angles now, upon examination of the spinners, you know that the first angle is \(30^{\circ}\), the second angle is \(45^{\circ}\), and the third angle is \(60^{\circ}\).
Graph \(210^{\circ}\) and identify its reference angle.
Solution
The graph of \(210^{\circ}\) looks like this:
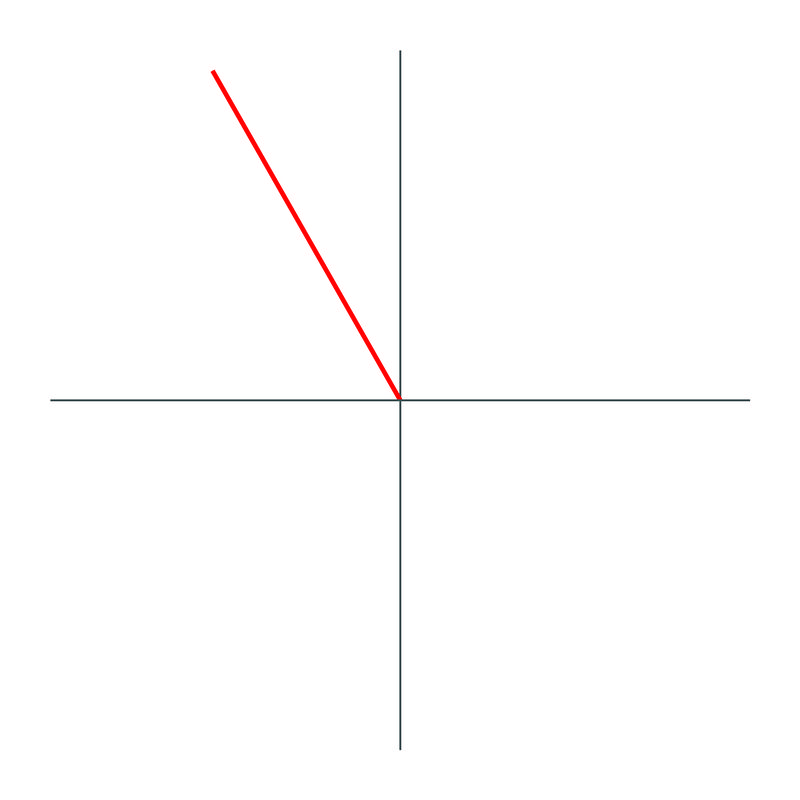
and since the angle makes a \(30^{\circ}\) angle with the negative "\(x\)" axis, the reference angle is \(30^{\circ}\).
Graph \(315^{\circ}\) and identify its reference angle.
Solution
The graph of \(315^{\circ}\) looks like this:
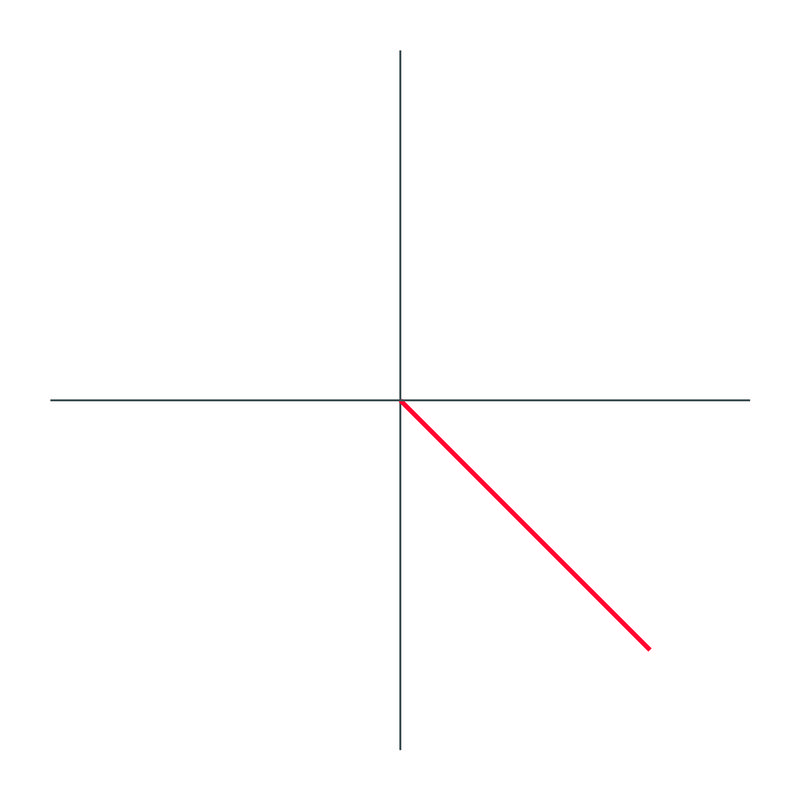
and since the angle makes a \(45^{\circ}\) angle with the positive "\(x\)" axis, the reference angle is \(45^{\circ}\).
Find the ordered pair for \(150^{\circ}\) and use it to find the value of cos \(150^{\circ}\).
Solution
Since the reference angle is \(30^{\circ}\), we know that the coordinates for the point on the unit circle are \(\left(−\dfrac{\sqrt{3}}{2}, \dfrac{1}{2}\right)\). This is the same as the value for \(30^{\circ}\), except the "\(x\)" coordinate is negative instead of positive. Knowing this,
\(\cos 150^{\circ}=\dfrac{\text { adjacent }}{\text { hypotenuse }}=\dfrac{-\dfrac{\sqrt{3}}{2}}{1}=-\dfrac{\sqrt{3}}{2}\)
Review
- Graph \(100^{\circ}\) and identify its reference angle.
- Graph \(200^{\circ}\) and identify its reference angle.
- Graph \(290^{\circ}\) and identify its reference angle.
Calculate each value using the unit circle and special right triangles.
- \(\sin 120^{\circ}\)
- \(\cos 120^{\circ}\)
- \(\csc 120^{\circ}\)
- \(\cos 135^{\circ}\)
- \(\sin 135^{\circ}\)
- \(\tan 135^{\circ}\)
- \(\sin 210^{\circ}\)
- \(\cos 210^{\circ}\)
- \(\cot 210^{\circ}\)\)
- \(\sin 225^{\circ}\)
- \(\cos 225^{\circ}\)
- \(\sec 225^{\circ}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 1.18.
Vocabulary
| Term | Definition |
|---|---|
| Reference Angle | A reference angle is the angle formed between the terminal side of the angle and the closest of either the positive or negative \(x\)-axis. |

