2.3.8: Trigonometric Functions of Negative Angles
- Page ID
- 14459
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Angles measured by rotating clockwise from the positive \(x\)-axis.
While practicing for the track team, you regularly stop to consider the values of trig functions for the angle you've covered as you run around the circular track at your school. Today, however, is different. To keep things more interesting, your coach has decided to have you and your teammates run the opposite of the usual direction on the track. From your studies at school, you know that this is the equivalent of a "negative angle".
You have run \(−45^{\circ}\) around the track, and want to fine the value of the cosine function for this angle. Is it still possible to find the values of trig functions for these new types of angles?
Trigonometric Functions of Negative Angles
Recall that graphing a negative angle means rotating clockwise. The graph below shows \(−30^{\circ}\).
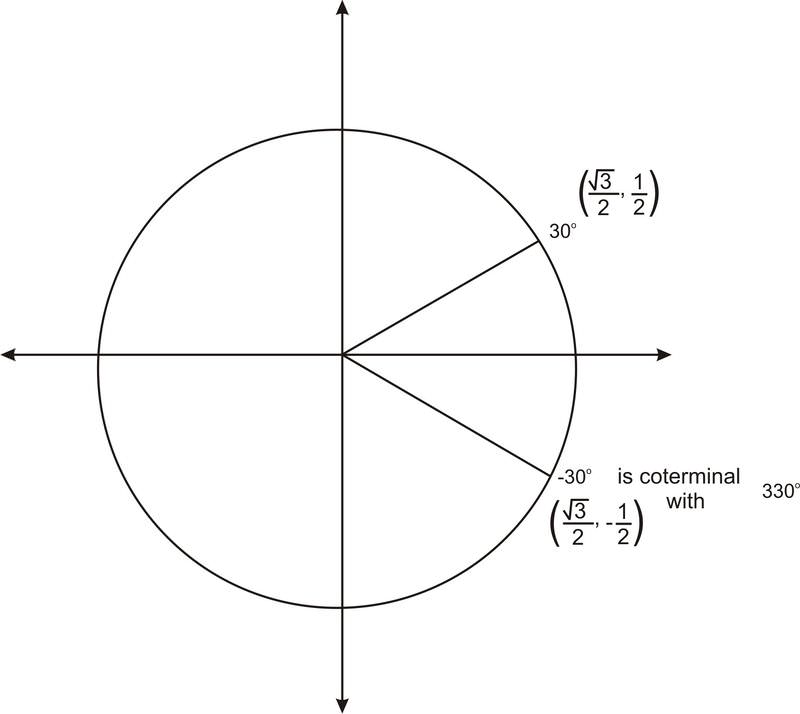
Notice that this angle is coterminal with \(330^{\circ}\). So the ordered pair is \(\left(\dfrac{\sqrt{3}}{2},−\dfrac{1}{2} \right)\). We can use this ordered pair to find the values of any of the trig functions of \(−30^{\circ}\). For example, \(\cos(−30^{\circ})=x=\dfrac{\sqrt{3}}{2}\).
In general, if a negative angle has a reference angle of \(30^{\circ}\), \(45^{\circ}\), or \(60^{\circ}\), or if it is a quadrantal angle, we can find its ordered pair, and so we can determine the values of any of the trig functions of the angle.
Finding the Value of Trigonometric Expressions
Find the value of the following expressions:
1. \(\sin(−45^{\circ} )\)
\(\sin(−45^{\circ} )=−\dfrac{\sqrt{2}}{2}\)
\(−45^{\circ}\) is in the \(4^{th}\) quadrant, and has a reference angle of \(45^{\circ}\). That is, this angle is coterminal with \(315^{\circ}\). Therefore the ordered pair is \(\left(\dfrac{\sqrt{2}}{2},−\dfrac{\sqrt{2}}{2}\right)\) and the sine value is \(−\dfrac{\sqrt{2}}{2}\).
2. \(\sec(−300^{\circ} )\)
\(\sec(−300^{\circ} )=2\)
The angle \(−300^{\circ}\) is in the \(1^{st}\) quadrant and has a reference angle of \(60^{\circ}\). That is, this angle is coterminal with \(60^{\circ}\). Therefore the ordered pair is \(\left(\dfrac{1}{2}, \dfrac{\sqrt{3}}{2}\right)\) and the secant value is \(\dfrac{1}{x}=\dfrac{1}{\dfrac{1}{2}}=2\).
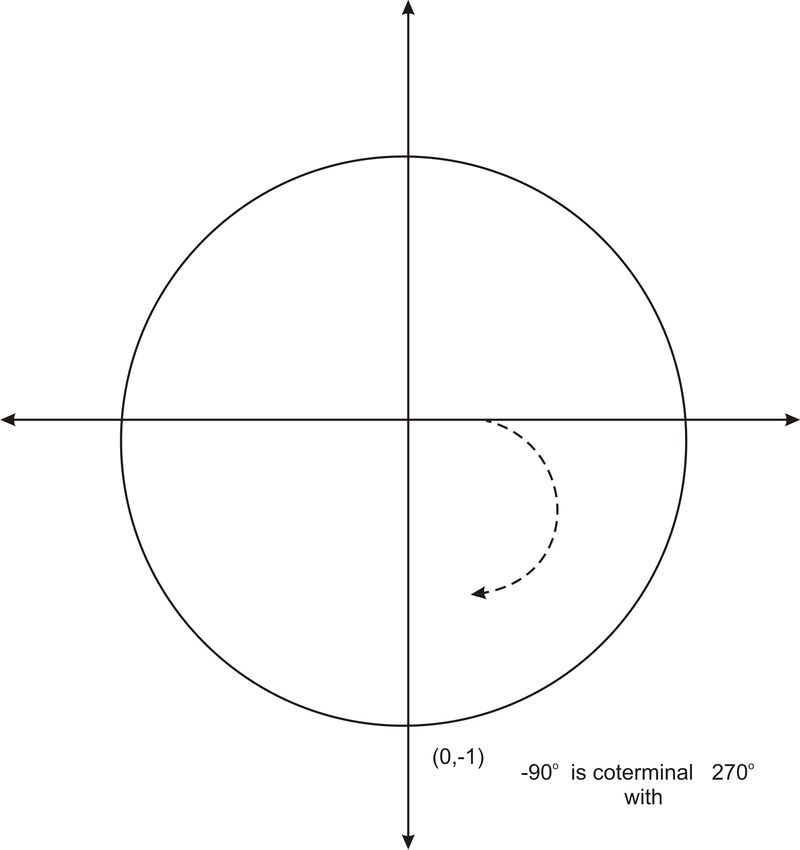
3. \(\cos(−90^{\circ} )\)
\(\cos(−90^{\circ} )=0\)
The angle −90^{\circ}\) is coterminal with \(270^{\circ}\). Therefore the ordered pair is (0, -1) and the cosine value is 0.
We can also use our knowledge of reference angles and ordered pairs to find the values of trig functions of angles with measure greater than 360 degrees.
Earlier, you were asked if it is still possible to find the values of trig functions for the new type of angles.
Solution
What you want to find is the value of the expression: \(\cos(−45^{\circ})\)
\(\cos(−45^{\circ} )=\dfrac{\sqrt{2}}{2}\)
\(−45^{\circ}\) is in the \(4^{th}\) quadrant, and has a reference angle of \(45^{\circ}\). That is, this angle is coterminal with \(315^{\circ}\). Therefore the ordered pair is \(\left(\dfrac{\sqrt{2}}{2},−\dfrac{\sqrt{2}}{2}\right)\) and the cosine value is \(\dfrac{\sqrt{2}}{2}\).
Find the value of the expression: \(\cos −180^{\circ}\)
Solution
The angle \(−180^{\circ}\) is coterminal with \(180^{\circ}\). Therefore the ordered pair of points is \((-1, 0)\). The cosine is the "x" coordinate, so here it is -1.
Find the value of the expression: \(\sin−90^{\circ}\)
Solution
The angle \(−90^{\circ}\) is coterminal with \(270^{\circ}\). Therefore the ordered pair of points is \((0, -1)\). The sine is the "\(y\)" coordinte, so here it is -1.
Find the value of the expression: \(\tan −270^{\circ}\)
Solution
The angle \(−270^{\circ}\) is coterminal with \(90^{\circ}\). Therefore the ordered pair of points is \((0, 1)\). The tangent is the "\(y\)" coordinate divided by the "\(x\)" coordinate. Since the "\(x\)" coordinate is 0, the tangent is undefined.
Review
Calculate each value.
- \(\sin −120^{\circ}\)
- \(\cos −120^{\circ}\)
- \(\tan −120^{\circ}\)
- \(\csc −120^{\circ}\)
- \(\sec −120^{\circ}\)
- \(\cot −120^{\circ}\)
- \(\csc −45^{\circ}\)
- \(\sec −45^{\circ}\)
- \(\tan −45^{\circ}\)
- \(\cos −135^{\circ}\)
- \(\csc −135^{\circ}\)
- \(\sec −135^{\circ}\)
- \(\tan −210^{\circ}\)
- \(\sin −270^{\circ}\)
- \(\cot −90^{\circ}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 1.19.
Vocabulary
| Term | Definition |
|---|---|
| Negative Angle | A negative angle is an angle measured by rotating clockwise (instead of counterclockwise) from the positive \(x\) axis. |

