4.1.8: Determination of Unknown Angles Using Law of Cosines
- Page ID
- 14872
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Find unknown angle given lengths of all 3 sides
Sarine draws a triangle. She measures the length of the sides and records her measurements as follows. What is the measure of angle \(C\) of the triangle?
\(\begin{aligned} a&=3 \\ b&=4 \\ c&=5 \end{aligned}\)
Law of Cosines with SSS
The Law of Cosines, \(a^2+b^2−2ab\cos C\), can be rearranged to facilitate the calculation of the measure of angle \(C\) when \(a\), \(b\) and \(c\) are all known lengths.
\(\begin{aligned} a^2+b^2−2ab \cos C &=c^2 \\ a^2+b^2−c^2 &=2ab\cos C\\ \dfrac{a^2+b^2−c^2}{2ab} &=\cos C \end{aligned}\)
which can be further manipulated to \(C=\cos ^{−1}\left(\dfrac{a^2+b^2−c^2 }{2ab}\right)\).
Let's find the measure of the largest angle in the triangle with side lengths 12, 18 and 21.
First, we must determine which angle will be the largest. Recall from Geometry that the longest side is opposite the largest angle. The longest side is 21 so we will let \(c=21\) since \(C\) is the angle we are trying to find. Let \(a=12\) and \(b=18\) and use the formula to solve for \(C\) as shown. It doesn’t matter which sides we assign to \(a\) and \(b\). They are interchangeable in the formula.
\(m\angle C=\cos ^{−1}\left(\dfrac{12^2+18^2−21^2 }{2(12)(18)}\right) \approx 86^{\circ}\)
Note: Be careful to put parenthesis around the entire numerator and entire denominator on the calculator to ensure the proper order of operations. Your calculator screen should look like this:
\(\cos ^{−1}((12^2+18^2−21^2)/(2(12)(18)))\)
Now let's find the value of \(x\), to the nearest degree.
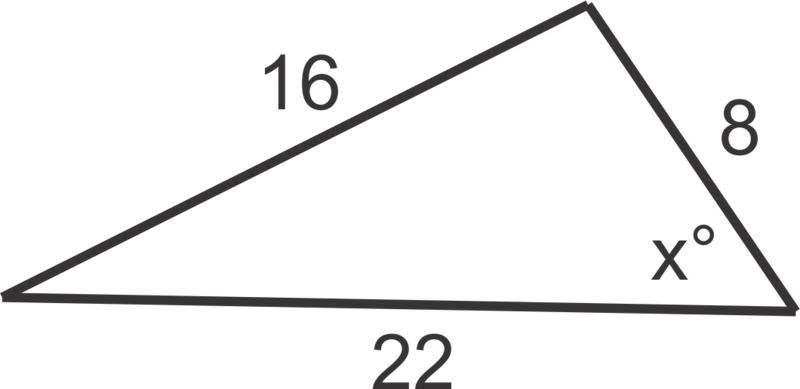
The angle with measure \(x^{\circ} \) will be angle \(C\) so \(c=16\), \(a=22\) and \(b=8\). Remember, \(a\) and \(b\) are interchangeable in the formula. Now we can replace the variables with the known measures and solve.
\(\cos ^{−1}\left(\dfrac{22^2+8^2−16^2}{2(22)(8)}\right)\approx 34^{\circ}\)
Finally, let's find the \(m\angle A\), if \(a=10\), \(b=15\) and \(c=21\).
First, let’s rearrange the formula to reflect the sides given and requested angle:
\(\cos A=\left(\dfrac{b^2+c^2−a^2}{2(b)(c)}\right)\), now plug in our values
\(m\angle A=\cos ^{−1}\left( \dfrac{15^2+21^2−10^2}{2(15)(21)}\right) \approx 26^{\circ}\)
Earlier, you were asked to find the measure of angle \(C\) of the triangle that has sides \(a = 3\), \(b = 4\), and \(c = 5\).
Solution
We can use the manipulated Law of Cosines to solve for \(C\).
\(\begin{aligned} C&=\cos ^{−1} \dfrac{3^2+4^2−5^2}{2(3)(4)} \\ C&=\cos ^{−1} \dfrac{9+16−25}{24} \\ C&=\cos ^{−1} \dfrac{0}{24}=\cos ^{−1} 0 \\ C&=90^{\circ} \end{aligned}\)
Therefore, the triangle is a right triangle.
Find the measure of \(x\) in the diagram:
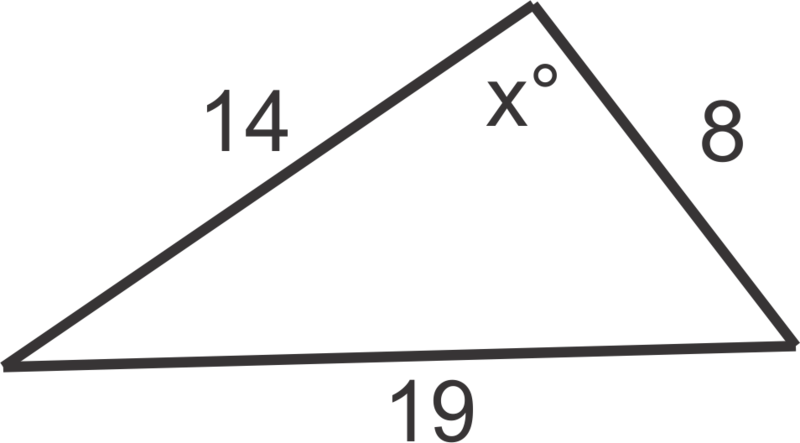
Solution
\(\cos ^{−1}\left(\dfrac{14^2+8^2−19^2}{2(14)(8)}\right) \approx 117^{\circ}\)
Find the measure of the smallest angle in the triangle with side lengths 47, 54 and 72.
Solution
The smallest angle will be opposite the side with length 47, so this will be our \(c\) in the equation.
\(\cos ^{−1}\left(\dfrac{54^2+72^2−47^2 }{2(54)(72)}\right) \approx 41^{\circ}\)
Find \(m\angle B\), if \(a=68\), \(b=56\) and \(c=25\).
Solution
Rearrange the formula to solve for \(m\angle B\),
\(\cos B=\left(\dfrac{a^2+c^2−b^2}{2(a)(c)}\right)\); \(\cos ^{−1}\left(\dfrac{68^2+25^2−56^2}{2(68)(25)}\right)\approx 52^{\circ}\)
Review
Use the Law of Cosines to find the value of \(x\), to the nearest degree, in problems 1 through 6.
-
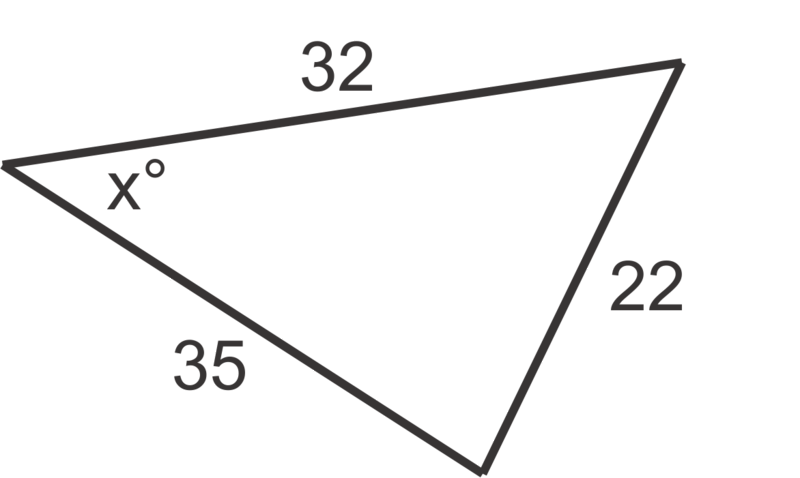
Figure \(\PageIndex{3}\) -
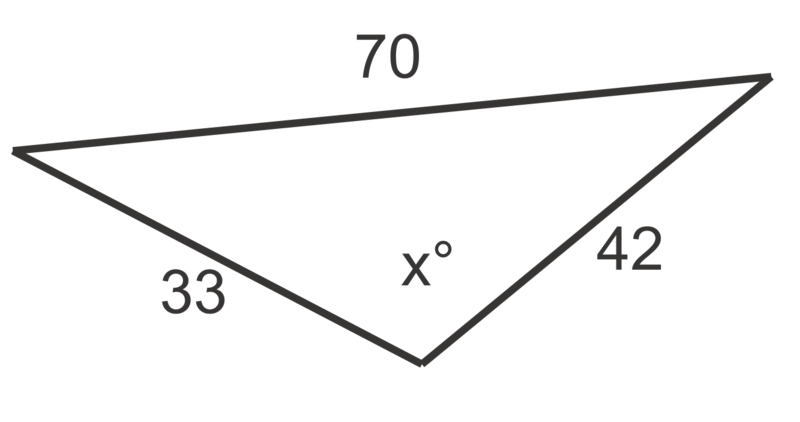
Figure \(\PageIndex{4}\) -
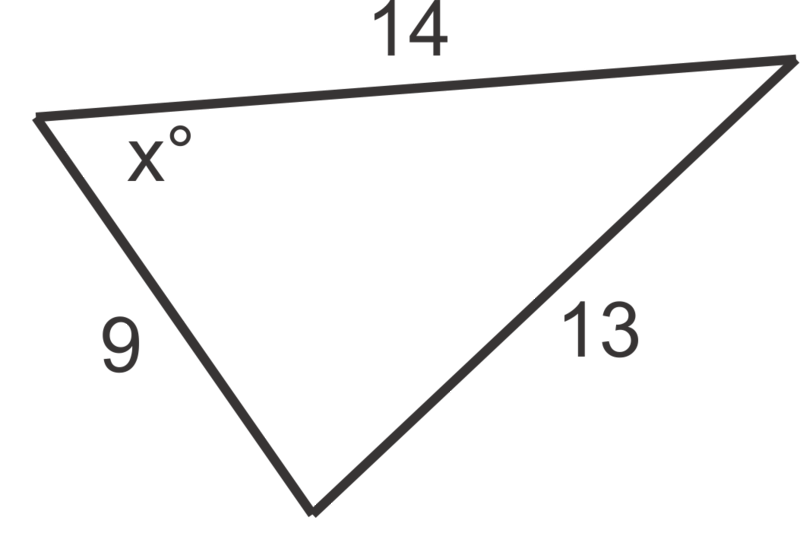
Figure \(\PageIndex{5}\) -
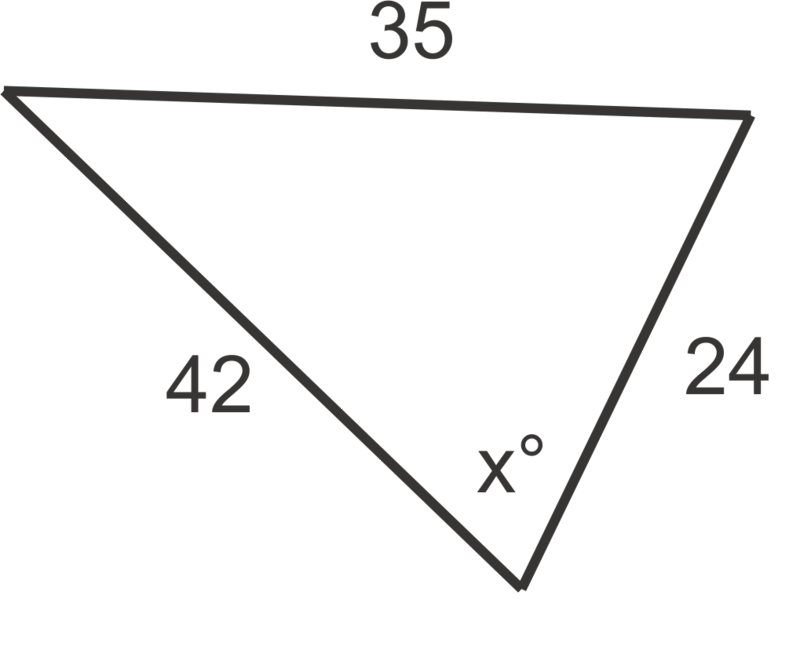
Figure \(\PageIndex{6}\) -
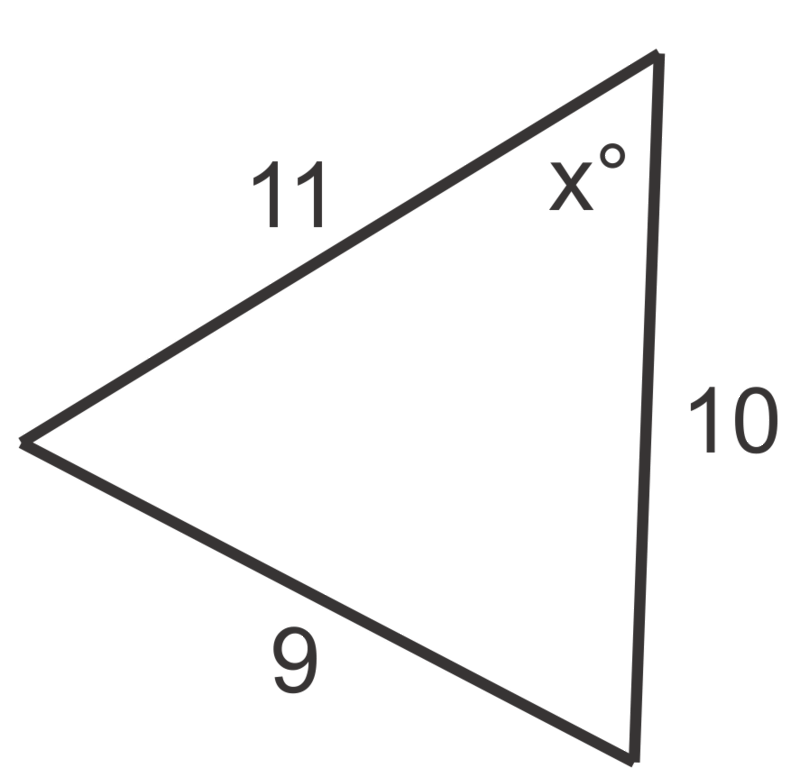
Figure \(\PageIndex{7}\) -
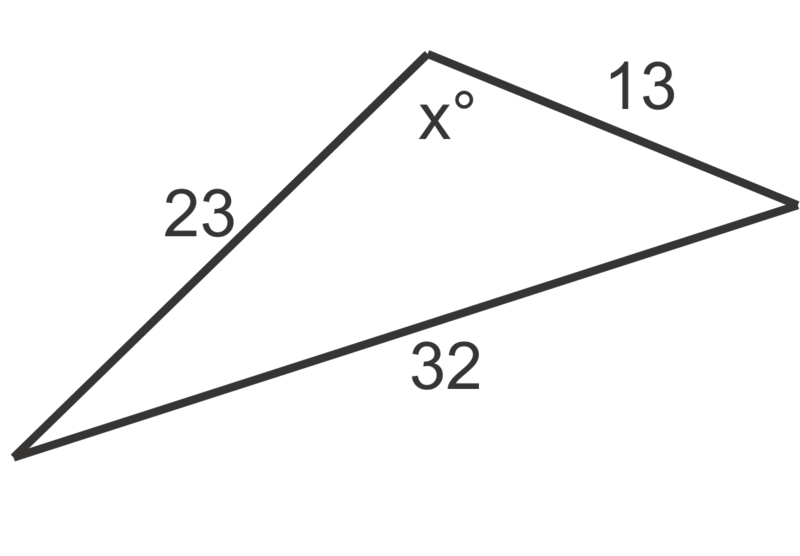
Figure \(\PageIndex{8}\) - Find the measure of the smallest angle in the triangle with side lengths 150, 165 and 200 meters.
- Find the measure of the largest angle in the triangle with side length 59, 83 and 100 yards.
- Find the \(m\angle C\) if \(a=6\), \(b=9\) and \(c=13\).
- Find the \(m\angle B\) if \(a=15\), \(b=8\) and \(c=9\).
- Find the \(m\angle A\) if \(a=24\), \(b=20\) and \(c=14\).
- A triangular plot of land is bordered by a road, a fence and a creek. If the stretch along the road is 100 meters, the length of the fence is 115 meters and the side along the creek is 90 meters, at what angle do the fence and road meet?
Answers for Review Problems
To see the Review answers, open this PDF file and look for section 13.16.
Additional Resources
Video: Example: Determine the Measure of an Angle of a Triangle Given the Length of Three Sides

