4.11: Third Angle Theorem
- Page ID
- 7423
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Third angles are equal if the other two sets are each congruent.
If two angles in one triangle are congruent to two angles in another triangle, then the third pair of angles must also congruent. This is called the Third Angle Theorem.
If \(\angle A\cong \angle D\) and \(\angle B\cong \angle E\), then \(\angle C\cong \angle F\).
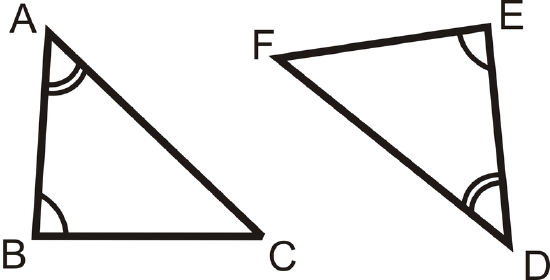
What if you were given \(\Delta FGH\) and \(\Delta XYZ\) and you were told that \(\angle F\cong \angle X\) and \(\angle G\cong \angle Y\)? What conclusion could you draw about \(\angle H\) and \(\angle Z\)?
Example \(\PageIndex{1}\)
Determine the measure of all the angles in each triangle.
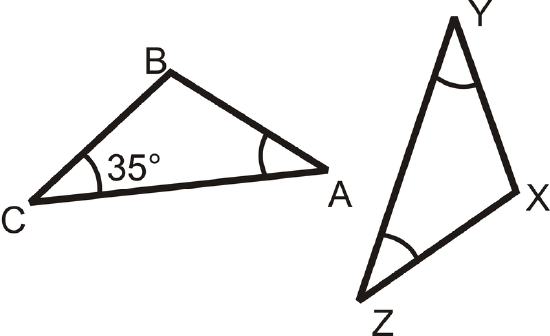
Solution
\(m\angle C=m\angle A=m\angle Y=m\angle Z=35\). By the Triangle Sum Theorem \(m\angle B=m\angle X=110\).
Example \(\PageIndex{2}\)
Determine the measure of all the angles in each triangle.
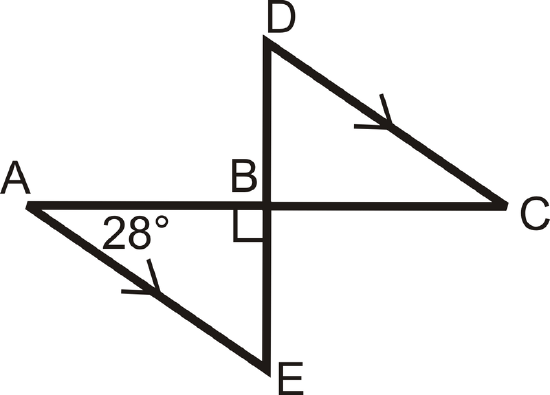
Solution
\(m\angle A=28\), \(m\angle ABE=90\) and by the Triangle Sum Theorem, \(m\angle E=62\). \(m\angle D=m\angle E=62\) because they are alternate interior angles and the lines are parallel. \(m\angle C=m\angle A=28\) because they are alternate interior angles and the lines are parallel. \(m\angle DBC=m\angle ABE=90\) because they are vertical angles.
Example \(\PageIndex{3}\)
Determine the measure of the missing angles.
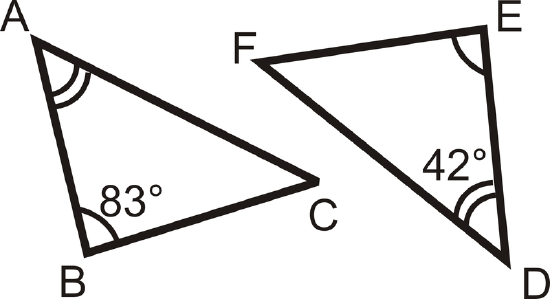
Solution
From the Third Angle Theorem, we know \(\angle C\cong \angle F\). From the Triangle Sum Theorem, we know that the sum of the interior angles in each triangle is \(180^{\circ}\).
\(\begin{align*} m\angle A+m\angle B+m\angle C &=180^{\circ} \\ m\angle D+m\angle B+m\angle C=180^{\circ} \\ 42^{\circ}+83^{\circ}+m\angle C &=180^{\circ}\\ m\angle C &=55^{\circ}=m\angle F\end{align*}\)
Example \(\PageIndex{4}\)
Explain why the Third Angle Theorem works.
Solution
The Third Angle Theorem is really like an extension of the Triangle Sum Theorem. Once you know two angles in a triangle, you automatically know the third because of the Triangle Sum Theorem. This means that if you have two triangles with two pairs of angles congruent between them, when you use the Triangle Sum Theorem on each triangle to come up with the third angle you will get the same answer both times. Therefore, the third pair of angles must also be congruent.
Example \(\PageIndex{5}\)
Determine the measure of all the angles in the triangle:
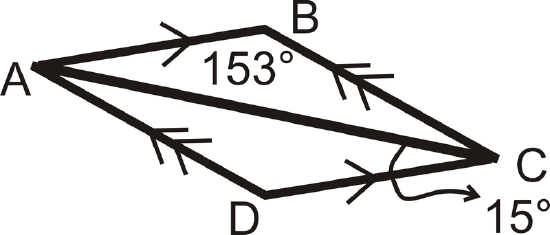
Solution
First we can see that \(m\angle DCA=15^{\circ}\). This means that \(m\angle BAC=15^{\circ}\) also because they are alternate interior angles. \(m\angle ABC=153^{\circ}\) was given. This means by the Triangle Sum Theorem that \(m\angle BCA=12^{\circ}\). This means that \(m\angle CAD=12^{\circ}\) also because they are alternate interior angles. Finally, \(m\angle ADC=153^{\circ}\) by the Triangle Sum Theorem.
Review
Determine the measures of the unknown angles.
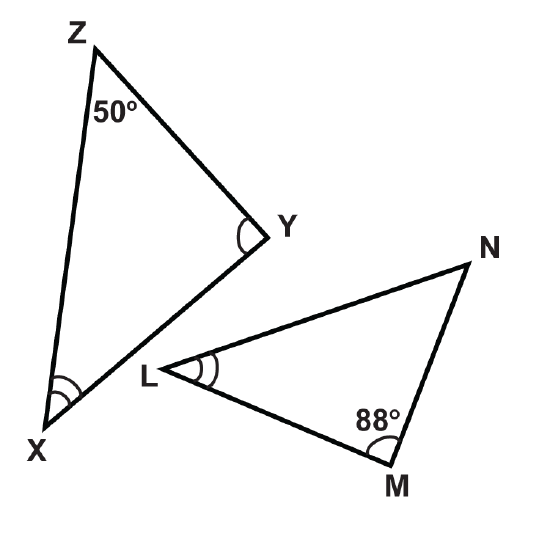
- \(\angle Y\)
- \(\angle x\)
- \(\angle N\)
- \(\angle L\)
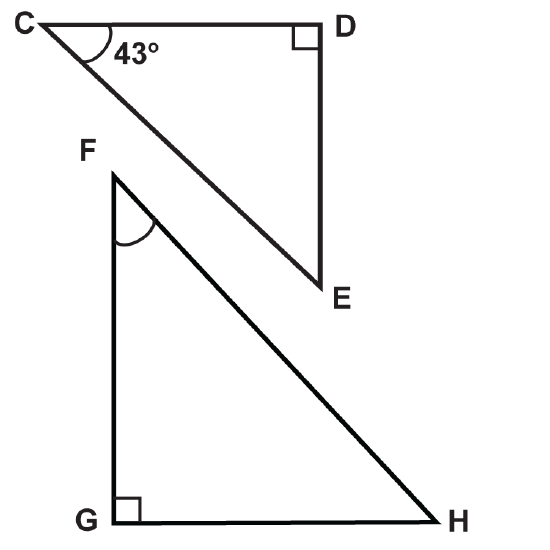
- \(\angle E\)
- \(\angle F\)
- \(\angle H\)
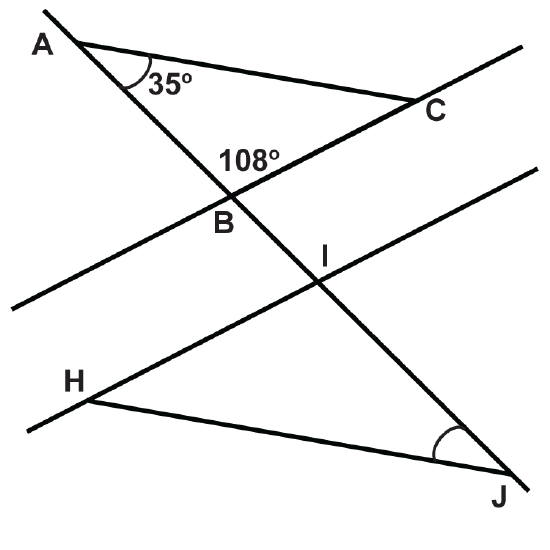
You may assume that \(\overleftrightarrow{BC}\parallel\overleftrightarrow{HI}\).
- \(\angle ACB\)
- \(\angle HIJ\)
- \(\angle HJI\)
- \(\angle IHJ\)
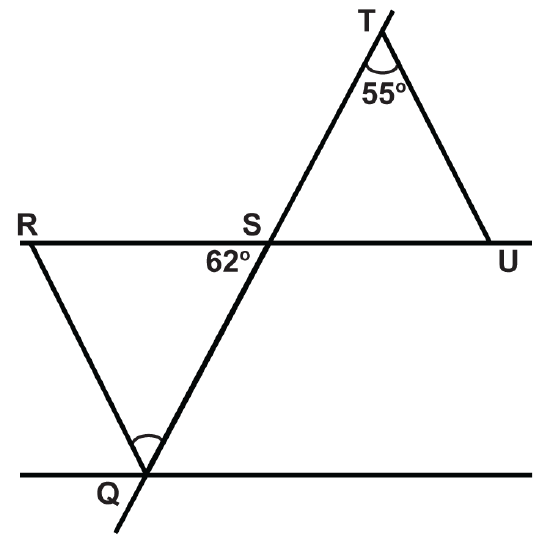
- \(\angle RQS\)
- \(\angle SRQ\)
- \(\angle TSU\)
- \(\angle TUS\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 4.5.
Vocabulary
| Term | Definition |
|---|---|
| Triangle Sum Theorem | The Triangle Sum Theorem states that the measure of the three interior angles of any triangle will add up to \(180^{\circ}\). |
| Third Angle Theorem | If two angles in one triangle are congruent to two angles in another triangle, then the third pair of angles is also congruent. |
Additional Resources
Video: The Third Angle Theorem Principles - Basic
Activities: Third Angle Theorem Discussion Questions
Study Aids: Triangle Congruence Study Guide
Practice: Third Angle Theorem
Real World: Third Angle Theorem
- \(\angle RQS\)
- \(\angle SRQ\)
- \(\angle TSU\)
- \(\angle TUS\)

