4.10: Congruence Statements

Corresponding angles and sides of congruent triangles are congruent.

When stating that two triangles are congruent, the corresponding parts must be written in the same order. For example, if we know that $\Delta ABC$ and $\Delta LMN$ are congruent then we know that:

Figure $\PageIndex{1}$

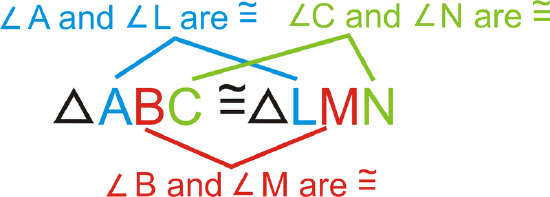
Notice that the congruent sides also line up within the congruence statement.

$\overline{AB} \cong \overline{LM}$, $\overline{BC} \cong \overline{MN}$, $\overline{AC} \cong \overline{LN}$

We can also write this congruence statement five other ways, as long as the congruent angles match up. For example, we can also write $\Delta ABC\cong \Delta LMN$ as:

$\begin{align*} \Delta ACB\cong \Delta LNM &\qquad& \Delta BCA\cong \Delta MNL &\qquad& \Delta BAC\cong \Delta MLN \\ \Delta CBA\cong \Delta NML &\qquad& \Delta CAB\cong \Delta NLM \end{align*}$

What if you were told that $\Delta FGH\cong \Delta XYZ$? How could you determine which side in $\Delta XYZ$ is congruent to $\overline{GH}$ and which angle is congruent to $\angle F$?

Example $\PageIndex{1}$

If $\Delta ABC\cong \Delta DEF$, what else do you know?

Solution

From this congruence statement, we know three pairs of angles and three pairs of sides are congruent.

$\angle A\cong \angle D,\angle B\cong \angle E$,\angle C\cong \angle F\),

$\overline{AB} \cong \overline{DE} , \overline{BC} \cong \overline{EF} , \overline{AC} \cong \overline{DF}$.

Example $\PageIndex{2}$

If$\Delta KBP\cong \Delta MRS$, what else do you know?

Solution

From this congruence statement, we know three pairs of angles and three pairs of sides are congruent.

$\angle K\cong \angle M,\:\angle B\cong \angle R,\:\angle P\cong \angle S$,

$\overline{KB} \cong \overline{MR} ,\:\overline{BP} \cong \overline{RS}, \: \overline{KP} \cong \overline{MS}$.

Example $\PageIndex{3}$

Write a congruence statement for the two triangles below.

Figure $\PageIndex{2}$

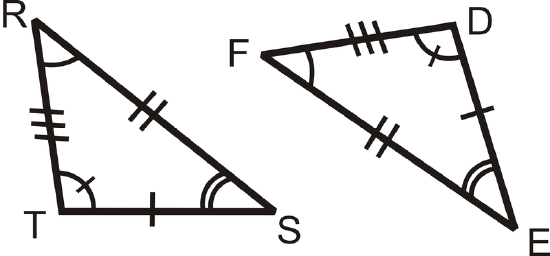
Solution

Line up the corresponding angles in the triangles:

$\angle R\cong \angle F,\:\angle S\cong \angle E\:and \angle T\cong \angle D$.

Therefore, one possible congruence statement is $\Delta RST\cong \angle FED$

Example $\PageIndex{4}$

If $\Delta CAT\cong \Delta DOG$, what else do you know?

Solution

From this congruence statement, we know three pairs of angles and three pairs of sides are congruent.

Figure $\PageIndex{3}$

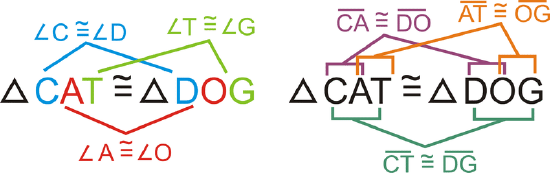
Example $\PageIndex{5}$

If $\Delta BUG\cong \Delta ANT$, what angle is congruent to $\angle N$?

Solution

Since the order of the letters in the congruence statement tells us which angles are congruent, $\angle N\cong \angle U$ because they are each the second of the three letters.

Review

For questions 1-4, determine if the triangles are congruent using the definition of congruent triangles. If they are, write the congruence statement.

1. 

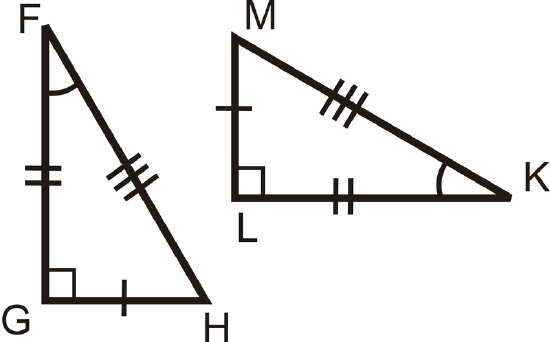
   Figure $\PageIndex{4}$

2. 

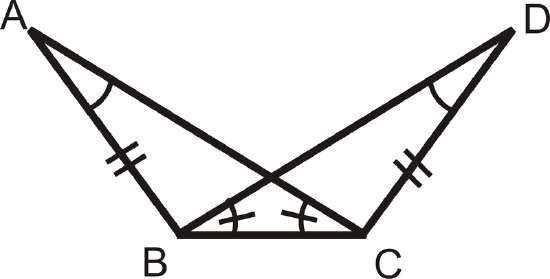
   Figure $\PageIndex{5}$

3. 

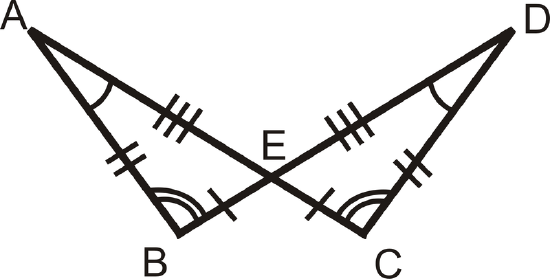
   Figure $\PageIndex{6}$

4. 

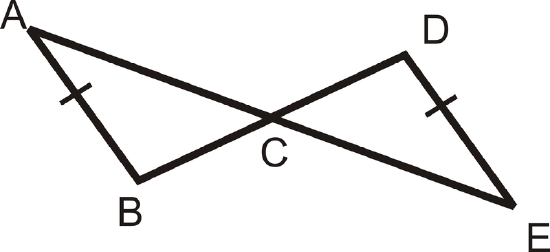
   Figure $\PageIndex{7}$

5. Suppose the two triangles below are congruent. Write a congruence statement for these triangles.

   

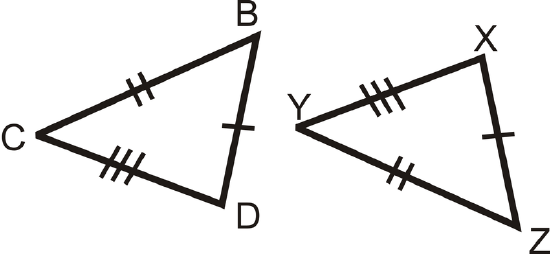
   Figure $\PageIndex{8}$

6. Explain how we know that if the two triangles are congruent, then $\angle B\cong \angle Z$.
7. If $\Delta TBS\cong \Delta FAM$, what else do you know?
8. If $\Delta PAM\cong \Delta STE$, what else do you know?
9. If $\Delta INT\cong \Delta WEB$, what else do you know?
10. If $\Delta ADG\cong \Delta BCE$, what angle is congruent to $\angle G$?

Review (Answers)

To see the Review answers, open this PDF file and look for section 4.4.

Resources

Additional Resources

Video: Introduction to Congruent Triangles

Activities: Congruence Statements Discussion Questions

Study Aids: Triangle Congruence Study Guide

Practice: Congruence Statements

Real World: Congruent Statements