4.9: CPCTC
- Page ID
- 4805
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Sides and angles of congruent triangles have the same measure.
Congruent Triangles
Two figures are congruent if they have exactly the same size and shape. If two triangles are congruent, they will have exactly the same three sides and exactly the same three angles. In other words, two triangles are congruent if you can turn, flip, and/or slide one so it fits exactly on the other.
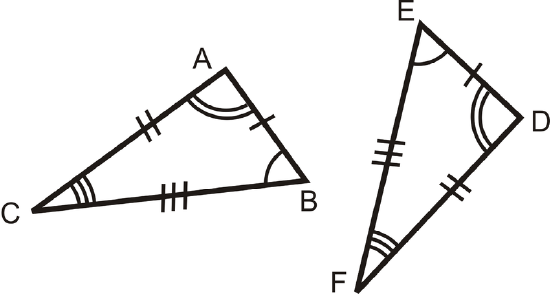
\(\Delta ABC\) and \(\Delta DEF\) are congruent because
\(\begin{align*}\overline{AB}\cong DE &\qquad& \angle A\cong \angle D \\ \overline{BC}\cong EF\overline{AB}&\:and\:& \angle B\cong \angle E \\ \overline{AC}\cong \overline{DF} &\qquad& \angle C\cong \angle F \end{align*}\)
Notice that when two triangles are congruent their three pairs of corresponding angles and their three pairs of corresponding sides are congruent.
When referring to corresponding congruent parts of congruent triangles, you can use the phrase Corresponding Parts of Congruent Triangles are Congruent, or its abbreviation CPCTC.
What if you were given two triangles with all the angle measures and all the side lengths marked? How could you tell if the two triangles were congruent?
Example \(\PageIndex{1}\)
Determine if the triangles are congruent using the definition of congruent triangles.
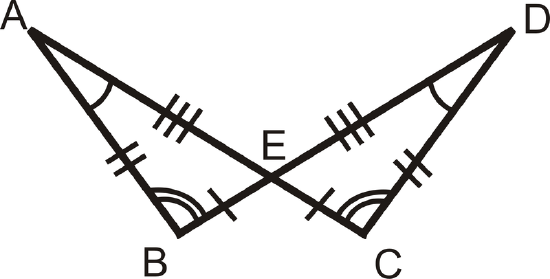
Solution
We can see from the markings that \(\angle B\cong \angle C\), \(\angle A\cong \angle D\), and \(\angle AEB\cong \angle DEC\) because they are vertical angles. Also, we know that \(\overline{BA}\cong \overline{CD}\), \(\overline{EA}\cong \overline{ED}\), and \(\overline{BE}\cong \overline{CE}\). Because three pairs of sides and three pairs of angles are all congruent and they are corresponding parts, this means that the two triangles are congruent.
Example \(\PageIndex{2}\)
Determine if the triangles are congruent using the definition of congruent triangles.
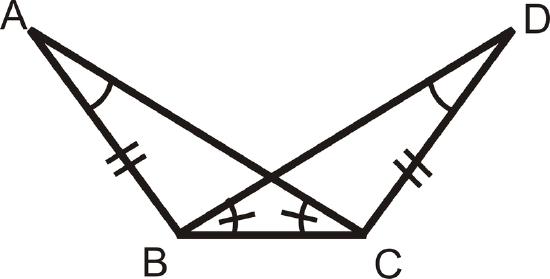
Solution
While there are congruent corresponding parts, there are only two pairs of congruent sides, the marked ones and the shared side. Without knowing whether or not the third pair of sides is congruent we cannot say if the triangles are congruent using the definition of congruent triangles. Note, this does not mean that the triangles are not congruent, it just means that we need more information in order to say they are congruent using the definition of congruent triangles (congruent triangles have three pairs of congruent angles and three pairs of congruent sides).
Example \(\PageIndex{3}\)
Are the two triangles below congruent?
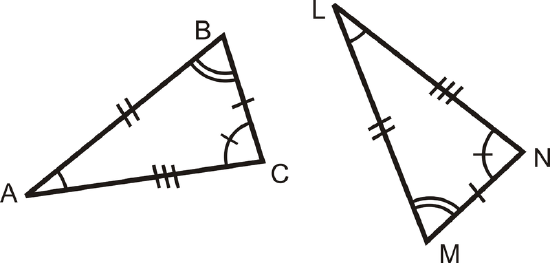
Solution
To determine if the triangles are congruent, match up sides with the same number of tic marks: \(\overline{BC}\cong \overline{MN}\), \(\overline{AB}\cong \overline{LM}\), \(\overline{AC}\cong \overline{LN}\).
Next match up the angles with the same markings:
\(\angle A\cong \angle L\), \(\angle B\cong \angle M\), and \(\angle C\cong \angle N\).
Lastly, we need to make sure these are corresponding parts. To do this, check to see if the congruent angles are opposite congruent sides. Here, \(\angle A\) is opposite \(\overline{BC}\) and \(\angle L\) is opposite \(\overline{MN}\). Because \(\angle A\cong \angle L\) and \(\overline{BC}\cong \overline{MN}\), they are corresponding. Doing this check for the other sides and angles, we see that everything matches up and the two triangles are congruent.
Example \(\PageIndex{4}\)
If all three pairs of angles for two given triangles are congruent does that mean that the triangles are congruent?
Solution
Without knowing anything about the lengths of the sides you cannot tell whether or not two triangles are congruent. The two triangles described above might be congruent, but we would need more information to know for sure.
Example \(\PageIndex{5}\)
Determine if the triangles are congruent using the definition of congruent triangles.
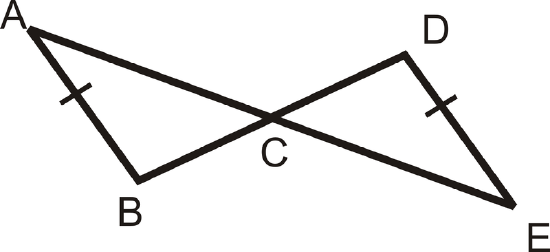
Solution
From the tic marks we can see that \(\overline{AB}\cong \overline{DE}\). We also know that \(\angle ACB\cong \angle ECD\) because they are vertical angles. However, this is not enough information to know whether or not the triangles are congruent.
Review
The following illustrations show two parallel lines cut by a transversal (You may assume that even though the lines are not marked parallel, the two lines that look parallel, actually are). Are the triangles formed by them definitively congruent?
-
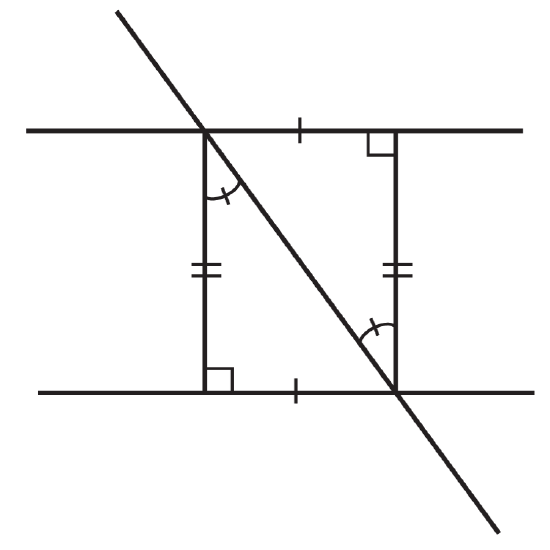
Figure \(\PageIndex{6}\) -
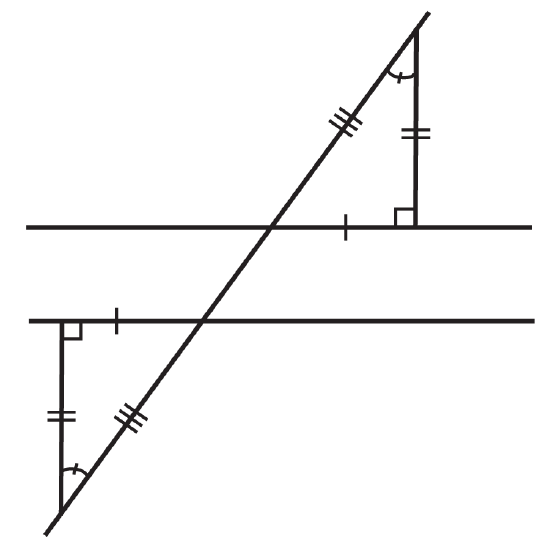
Figure \(\PageIndex{7}\) -
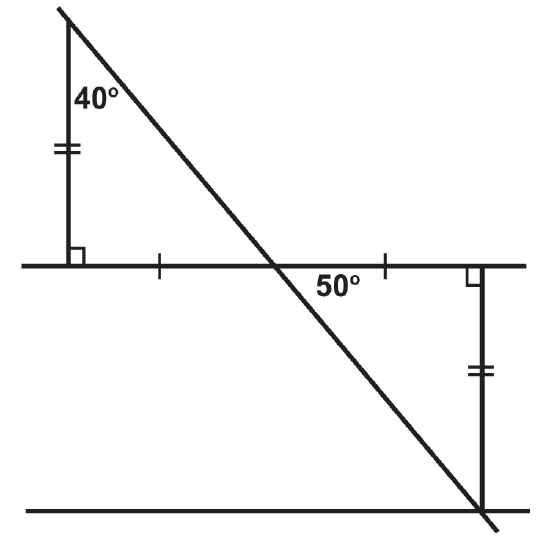
Figure \(\PageIndex{8}\) -
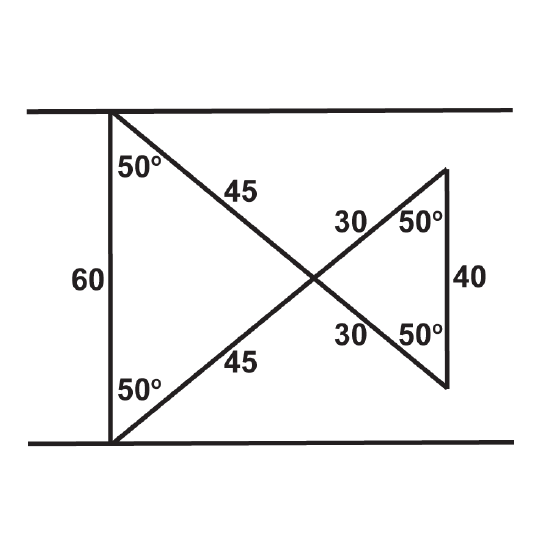
Figure \(\PageIndex{9}\) -
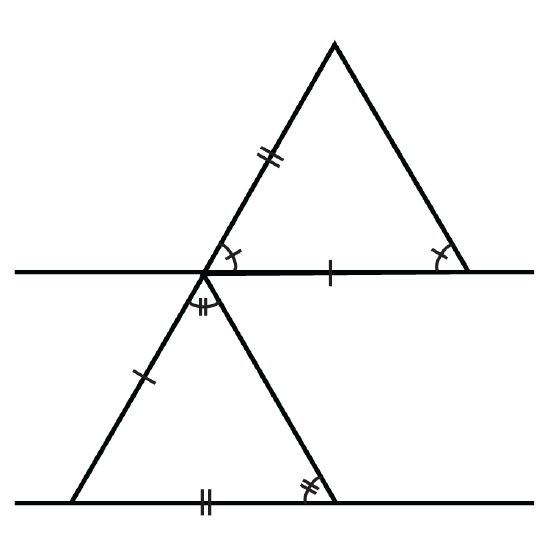
Figure \(\PageIndex{10}\)
Based on the following details, are the triangles definitively congruent?
- Both triangles are right triangles in which one angle measures \(55^{\circ}\). All of their corresponding sides are congruent.
- Both triangles are equiangular triangles.
- Both triangles are equilateral triangles. All sides are 5 inches in length.
- Both triangles are obtuse triangles in which one angle measures \(35^{\circ}\). Two of their corresponding sides are congruent.
- Both triangles are obtuse triangles in which two of their angles measure \(40^{\circ}\) and \(20^{\circ}\). All of their corresponding sides are congruent.
- Both triangles are isosceles triangles in which one angle measures \(15^{\circ}\).
- Both triangles are isosceles triangles with two equal angles of \(55^{\circ}\). All corresponding sides are congruent.
- Both triangles are acute triangles in which two of their angles measure \(40^{\circ}\) and \(80^{\circ}\). All of their corresponding sides are congruent.
- Both triangles are acute triangles in which one angle measures \(60^{\circ}\). Two of their corresponding sides are congruent.
- Both triangles are equilateral triangles.
Review (Answers)
To see the Review answers, open this PDF file and look for section 4.3.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Third Angle Theorem | If two angles in one triangle are congruent to two angles in another triangle, then the third pair of angles is also congruent. |
Additional Resources
Interactive Element
Video: Congruent and Similar Triangles
Activities: Congruent Triangles Discussion Questions
Study Aids: Triangle Congruence Study Guide
Practice: CPCTC
Real World: Congruent Triangles

