4.5: Equilateral Triangles
- Page ID
- 2174
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Properties of triangles with three equal sides.
Equilateral Triangle Theorem: All equilateral triangles are also equiangular. Furthermore, all equiangular triangles are also equilateral.
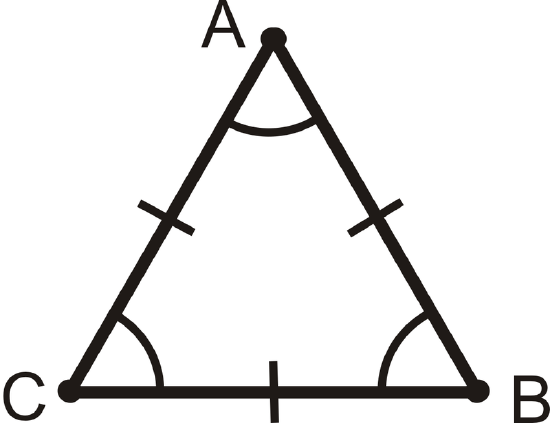
If \(\overline{AB}\cong \overline{BC}\cong \overline{AC}\), then \(\angle A\cong \angle B\cong \angle C\). Conversely, if \(\angle A\cong \angle B\cong \angle C\), then \(\overline{AB}\cong \overline{BC}\cong \overline{AC}\).
What if you were presented with an equilateral triangle and told that its sides measure \(x\), \(y\), and 8? What could you conclude about \(x\) and \(y\)?
Example \(\PageIndex{1}\)
Fill in the proof:
Given: Equilateral \(\Delta RST\) with
\(\overline{RT}\cong \overline{ST}\cong \overline{RS}\)
Prove: \(\Delta RST\) is equiangular
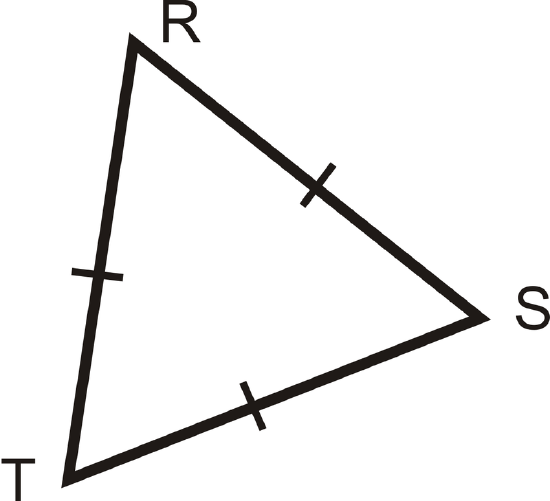
Solution
| Statement | Reason |
|---|---|
| 1. | 1. Given |
| 2. | 2. Base Angles Theorem |
| 3. | 3. Base Angles Theorem |
| 4. | 4. Transitive \(PoC\) |
| 5. \(\Delta RST\) is equiangular | 5. |
| Statement | Reason |
|---|---|
| 1. \(RT\overline{AB}\cong ST\overline{AB}\cong RS\overline{AB}\) | 1. Given |
| 2. \(\angle R\cong \angle S\) | 2. Base Angles Theorem |
| 3.\(\angle T\cong \angle R\) | 3. Base Angles Theorem |
| 4. \(\angle T\cong \angle S\) | 4. Transitive \(PoC\) |
| 5. \(\Delta RST\) is equiangular | 5. Definition of equiangular. |
Example \(\PageIndex{2}\)
True or false: All equilateral triangles are isosceles triangles.
Solution
This statement is true. The definition of an isosceles triangle is a triangle with at least two congruent sides. Since all equilateral triangles have three congruent sides, they fit the definition of an isosceles triangle.
Example \(\PageIndex{3}\)
Find the value of \(x\).
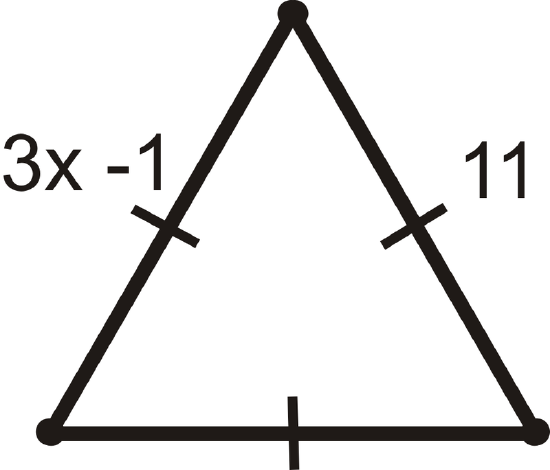
Solution
Because this is an equilateral triangle \(3x−1=11\). Solve for \(x\).
\(\bgin{align*} 3x−1&=11 \\3x&=12 \\ x&=4 \end{align*}\)
Example \(\PageIndex{4}\)
Find the values of \(x\) and \(y\).
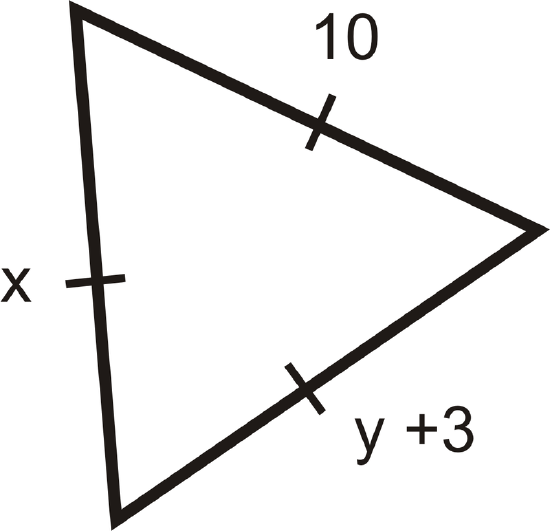
Solution
The markings show that this is an equilateral triangle since all sides are congruent. This means all sides must equal \(10\). We have \(x=10\) and \(y+3=10\) which means that \(y=7\).
Example \(\PageIndex{5}\)
Two sides of an equilateral triangle are \(2x+5\) units and \(x+13\) units. How long is each side of this triangle?
Solution
The two given sides must be equal because this is an equilateral triangle. Write and solve the equation for \(x\).
\(\egin{align*}2x+5 &=x+13 \\ x&=8 \end{align*}\)
To figure out how long each side is, plug in 8 for \(x\) in either of the original expressions. \(2(8)+5=21\). Each side is \(21\) units.
Review
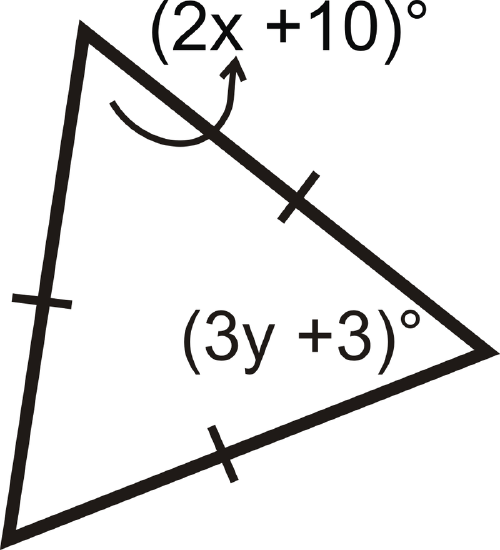
The following triangles are equilateral triangles. Solve for the unknown variables.
-
Figure \(\PageIndex{4}\) -
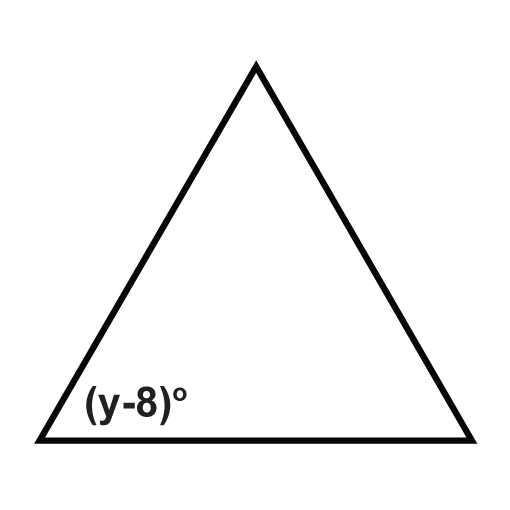
Figure \(\PageIndex{5}\) -
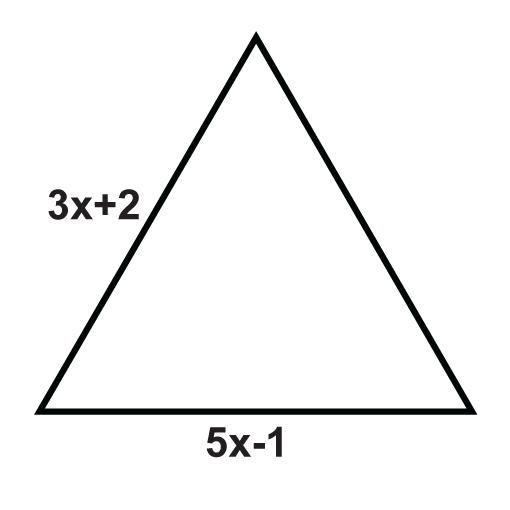
Figure \(\PageIndex{6}\) -
Figure \(\PageIndex{7}\) -
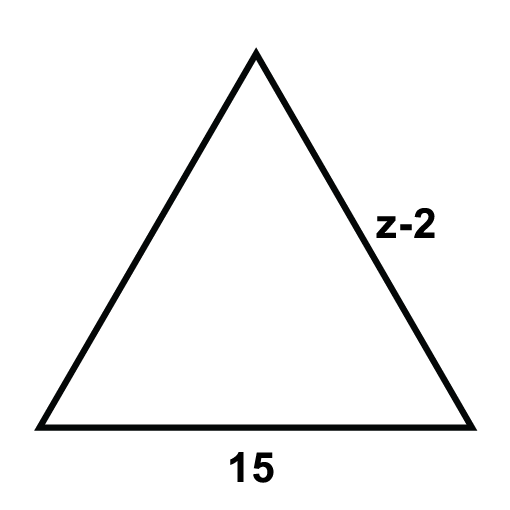
Figure \(\PageIndex{8}\) -
Figure \(\PageIndex{9}\) -
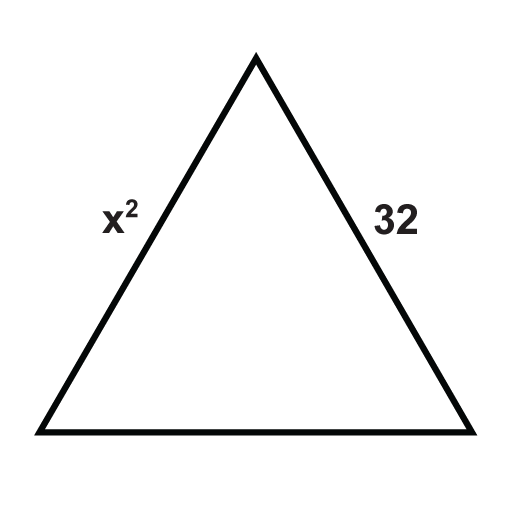
Figure \(\PageIndex{10}\) -
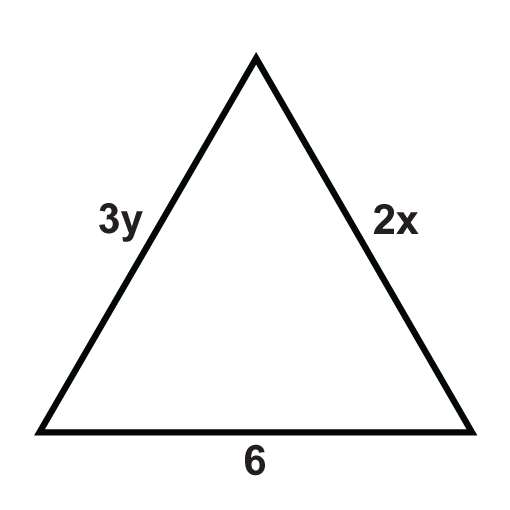
Figure \(\PageIndex{11}\) -
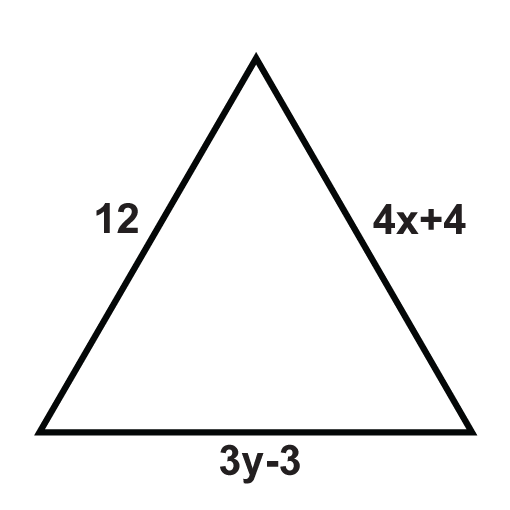
Figure \(\PageIndex{12}\) -
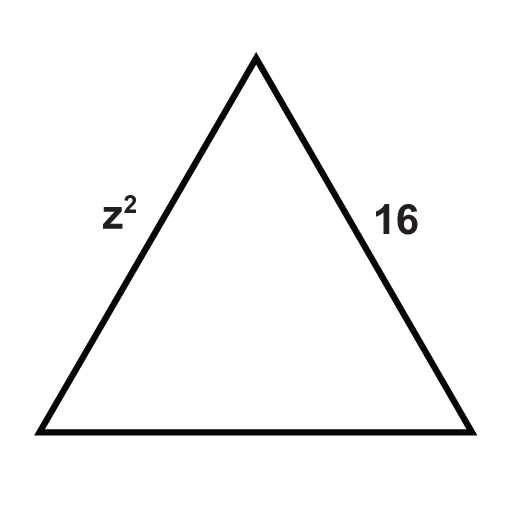
Figure \(\PageIndex{13}\) -
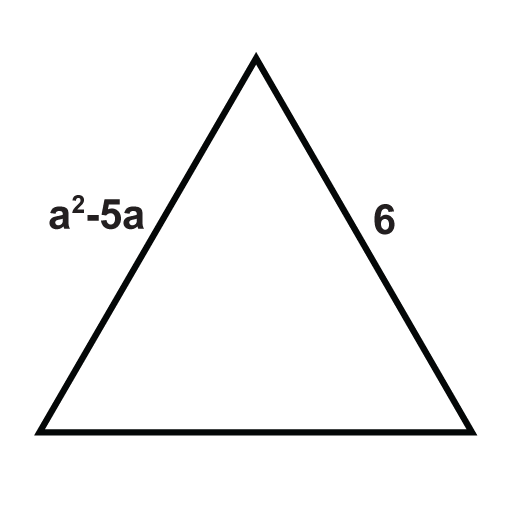
Figure \(\PageIndex{14}\) -
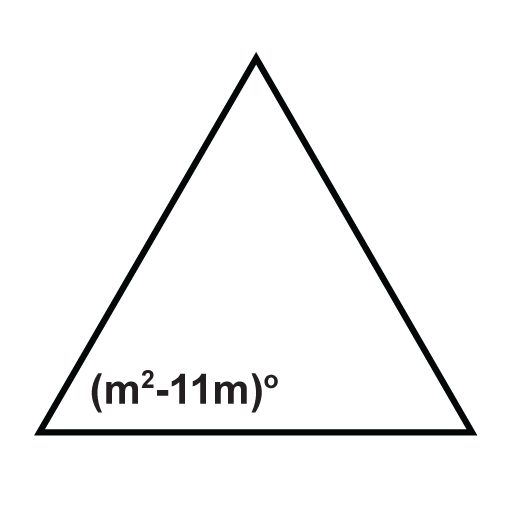
Figure \(\PageIndex{15}\) -
Figure \(\PageIndex{16}\) -
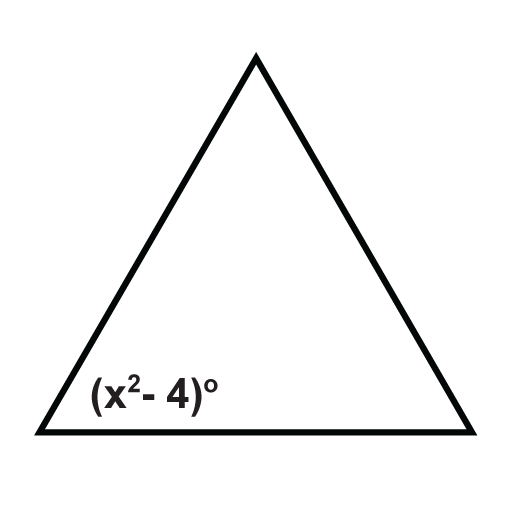
Figure \(\PageIndex{17}\) - Find the measures of \(x\) and \(y\).
Review (Answers)
To see the Review answers, open this PDF file and look for section 4.11.
Additional Resources
Interactive Element
Video: Equilateral Triangles Principles - Basic
Activities: Equilateral Triangles Discussion Questions
Study Aids: Equilateral Triangles Discussion Questions
Practice: Equilateral Triangles
Real World: Equilateral Triangles