5.25: Corresponding Parts of Congruent Figures
- Page ID
- 5009
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Identify matching side lengths and angle measures in congruent figures.

Melvin lives in a house that has a lot of mirrors. He enjoys looking in the mirrors and playing with the mirrors. One day, his mother tells him that the parallelogram shaped mirror by the front door is congruent to the parallelogram shaped mirror next to the pictures in the hallway. Melvin draws the to shapes as best as he can and labels the parts that he knows for each shape.
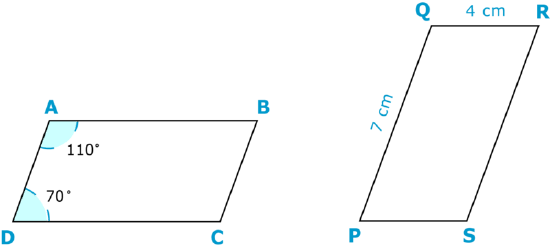
What is the length of \(\overline{AB}\)?
In this concept, you will learn about corresponding parts of congruent figures.
Corresponding Parts of Congruent Figures
The word corresponding refers to parts that match between two congruent triangles. You can identify corresponding angles and corresponding sides.

First, name the corresponding angles. Corresponding angles are matching angles between the two triangles. Corresponding angles will have the same measure in congruent triangles.
\(\angle A\cong \angle D\angle B\cong \angle E\angle C\cong \angle F\)
Here the angles are connected with the symbol for congruent. When you see the equals sign with a squiggly line on top, you know that the items on each side of the equation are congruent.
Next, name the corresponding sides. Corresponding sides are matching sides between two triangles. They will have the same length in congruent triangles.
\(\begin{aligned}\overline{AB}&\cong \overline{DE} \\ \overline{AC} &\cong \overline{DF} \\ \overline{BC} &\cong \overline{EF}\end{aligned}\)
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Melvin and his house of mirrors.
He learns that two of the mirrors are congruent, so he draws the shapes as best as he can and fills in what he knows about each shape.

What is the length of \(\overline{AB}\)?
Solution
First, rotate the second shape so that it looks the same as the first shape.
Next, identify the side on the second triangle that corresponds to \(\overline{AB}\).
\(\overline{PQ}\)
Then, write the length of the corresponding side.
7 cm
The answer is 7 cm. The length of \(\overline{AB}\) is 7 cm.
Example \(\PageIndex{2}\)
These two figures are congruent. Which angle is congruent to angle \(A\)?

Solution
First, turn the second figure so that it is arranged like the first shape.
Then, identify the angle on the second figure that is in the same position as angle \(A\) in the first triangle.
\(P\)
The answer is angle \(P\). \(\angle A\cong \angle P\)
Use the following diagram of two congruent triangles to answer the following questions.

Example \(\PageIndex{3}\)
Angle \(E\) is congruent to angle _____
Solution
First, make sure that the triangles are arranged so that they look the same.
Yes
Then, identify the angle on the second triangle that is in the position that angle \(E\) is in the first triangle.
\( H\)
The answer is angle \(H\). Angle \(E\) is congruent to angle \(H\).
Example \(\PageIndex{4}\)
\(\overline{FG}\cong ______\)
Solution
First, make sure that the triangles are arranged so that they look the same.
Yes
Then, identify the line segment on the second triangle that is in the position that \(\overline{FG}\) is in the first triangle.
\(\overline{IJ}\)
The answer is \(\overline{IJ}\). \(\overline{FG}\cong \overline{IJ}\).
Example \(\PageIndex{5}\)
Angle \(J\) is congruent to angle _____
Solution
First, make sure that the triangles are arranged so that they look the same.
Yes
Then, identify the angle on the second triangle that is in the position that angle J is in the first triangle.
\(G\)
The answer is angle \(G\). Angle \(J\) is congruent to angle \(G\).
Review
Use the following triangles to answer the questions.

- Are these two triangles similar or congruent?
- How do you know?
- Side \(DE\) is congruent to which other side?
- Side \(DF\) is congruent to which other side?
- Side \(EF\) is congruent to which other side?
- If the side length of DE is 10, what is the side length of \(GH\)?
- If the side length of HI is 8, which other side is also 8?
Use the following figures to answer the questions.

- These two figures are congruent. Explain two ways that you can determine whether or not figures are congruent.
- Angle \(Q\) is congruent to which other angle?
- Angle \(R\) is congruent to which other angle?
- Angle \(S\) is congruent to which other angle?
- If \(PQ\) is 7 cm, which other sides are 7 cm?
- If \(QR\) is 4 cm, which other sides are 4 cm?
- If Angle \(D\) is 70 degrees, name another 70 degree angle.
- If Angle \(A\) is 110 degrees, name another 110 degree angle.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Congruent | Congruent figures are identical in size, shape and measure. |
| Corresponding | The corresponding sides between two triangles are sides in the same relative position. |
| Similar | Two figures are similar if they have the same shape, but not necessarily the same size. |
Additional Resources
Video: Congruent and Similar Triangles
Practice: Corresponding Parts of Congruent Figures

