5.26: Determine Missing Angle Measures
- Page ID
- 5010
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Find missing angle measures of quadrilaterals given a sum of 360 degrees.
Understanding the Angle Measures of Quadrilaterals

Stephanie, a Math 12 student, is helping to raise money to participate in this year’s Math Olympiad in Dallas, Texas. Since Stephanie is very artistic in making jewelry, she has decided to make and sell necklaces to raise money. Several customers have asked her what shape she has used for the blue bead of a particularly geometric looking necklace. She knows what shape it is but is not sure of how to explain this shape to her customers.
What can Stephanie tell her customers about this shape?
In this concept, you will learn to understand the angle measures of quadrilaterals.
Quadrilaterals
A quadrilateral is a two-dimensional closed shape that has four straight sides.
Three special quadrilaterals are a parallelogram which is a quadrilateral with opposite sides parallel and congruent, a trapezoid which is a quadrilateral that has one pair of opposite sides parallel and a kite which is a quadrilateral that has two pairs of congruent adjacent sides.
Three special parallelograms are a rectangle which has every angle a right angle and opposite sides both congruent and parallel, a square which has every angle a right angle, opposite sides parallel and all sides congruent and a rhombus which has every side equal in length, opposite sides parallel, but not every angle is a right angle.
Remember a quadrilateral is a two-dimensional closed shape that has four straight sides and four angles.
The sum of the interior angles of a quadrilateral is \(360^{\circ}\) regardless of the type of quadrilateral. The following diagram will show various quadrilaterals and their interior angles.
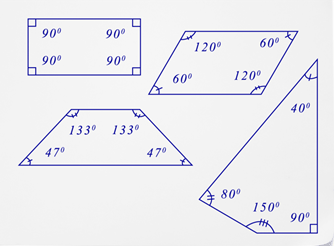
If you add the measure of the four interior angles of each quadrilateral shown above, the sum will equal \(360^{\circ}\). Each of these quadrilaterals can be divided into two triangles. Remember the sum of the interior angles of a triangle equals \(180^{\circ}\). If the closed figure contains two triangles then the sum of the interior angles equals \(2(180^{\circ})=360^{\circ}\).
Let’s apply these facts to an example.
For the following quadrilateral, determine the measure of \angle M\).
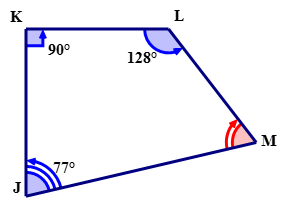
First, write an equation to represent the sum of the interior angles of quadrilateral \(JKLM\).
\(\angle J+\angle K+\angle L+\angle M=360^{\circ}\)
Next, substitute into the equation, the given measures of angles J\),K\) and L\).
\(\begin{aligned} \angle J+\angle K+\angle L+\angle M &=360^{\circ} \\ 77^{\circ}+90^{\circ}+128^{\circ}+\angle M &=360^{\circ} \end{aligned}\)
Next, simplify the left side of the equation.
\(\begin{aligned}77^{\circ}+90^{\circ}+128^{\circ}+\angle M&=360^{\circ} \\ 295^{\circ}+\angle M&=360^{\circ}\end{aligned}\)
Then, subtract \(295^{\circ}\) from both sides of the equation to solve for the measure of \(\angle M\).
\(\begin{aligned} 295^{\circ}+\angle M &=360^{\circ} \\ 295^{\circ}−295^{\circ}+\angle M &=360^{\circ}−295^{\circ} \\ \angle M &=65^{\circ} \end{aligned}\)
The answer is 65.
The measure of \(\angle M\) is \(65^{\circ}\).
This method can be used to calculate the measure of the missing angle of any quadrilateral when the measures of three of the angles are known.
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Stephanie and her necklaces. She needs to figure out what to tell her customers about the shape of the blue bead. What can she tell them?
Solution
First, draw the shape and include all important markings.
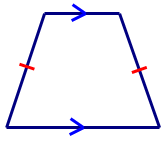
Next, explain the markings on the sides of the shape.
The arrows on the top and bottom sides of the figure indicate that this pair of opposite sides are parallel. The tic mark on the other two sides indicate that these sides are congruent (equal in length).
Then, name the shape.
The shape of the blue bead is an isosceles trapezoid.
Example \(\PageIndex{2}\)
A quadrilateral \(ABCD\) having one pair of opposite sides parallel has angle measures such that \(\angle A=44^{\circ}\). Find the measure of \(\angle C\) in the following quadrilateral.
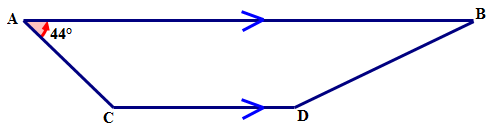
Solution
First, name the type of quadrilateral and write down what you know.
A quadrilateral with one pair of opposite sides parallel is called a trapezoid. \(\angle A\) and \(\angle C\) are on the same side of leg \(\angle AC\) and are supplementary.
Next, write an equation to model what you know about the two angles.
\(\angle A+\angle C=180^{\circ}\)
Next, fill into the equation the measure of \(\angle A\).
\(\begin{aligned} \angle A+\angle C&=180^{\circ} \\ 44^{\circ}+\angle C&=180^{\circ}\end{aligned}\)
Then, subtract \(44^{\circ}\) from both sides of the equation to solve for \angle C\).
\(\begin{aligned} 44^{\circ}+\angle C&=180^{\circ} \\ 44^{\circ}−44^{\circ}+\angle C&=180^{\circ}−44^{\circ} \\ \angle C &=136^{\circ} \end{aligned}\)
The answer is 136.
The measure of \(\angle C\) is \(136^{\circ}\).
Example \(\PageIndex{3}\)
For the following quadrilateral, find the measure of the unknown angle.
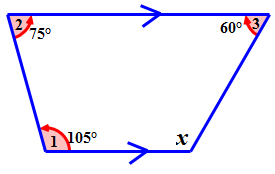
Solution
First, write an equation to model the sum of the interior angles of a quadrilateral.
\(\angle 1+\angle 2+\angle 3+\angle 4=360^{\circ}\)
Next, fill into the equation the measures of any known angles.
\(\begin{aligned} \angle 1+\angle 2+\angle 3+\angle 4 &=360^{\circ} \\ 105^{\circ}+75^{\circ}+60^{\circ}+\angle 4&=360^{\circ} \end{aligned}\)
Next, let \(\angle 4=x\)
\(\begin{aligned} 105^{\circ}+75^{\circ}+60^{\circ}+\angle 4=360^{\circ} \\ 105^{\circ}+75^{\circ}+60^{\circ}+x=360^{\circ} \end{aligned}\)
Next, simplify the left side of the equation.
\(\begin{aligned}105^{\circ}+75^{\circ}+60^{\circ}+x&=360^{\circ} \\ 240^{\circ}+x&=360^{\circ} \end{aligned}\)
Next, subtract \(240^{\circ}\) from both sides of the equation to solve for ‘\(x\)’.
\(\begin{aligned} 240^{\circ}+x&=360^{\circ} \\ 240^{\circ}−240^{\circ}+x&=360^{\circ} \\ x&=360^{\circ}−240^{\circ}=120^{\circ} \end{aligned}\)
The answer is 120.
The measure of \(\angle 4\) is \(120^{\circ}\).
Example \(\PageIndex{4}\)
What is the measure of the fourth angle of a quadrilateral which has three angles that measure \(110^{\circ}\), \(80^{\circ}\) and \(95^{\circ}\)?
Solution
First, write an equation to model the sum of the interior angles of the quadrilateral.
\(\angle 1+\angle 2+\angle 3+\angle 4=360^{\circ}\)
Next, fill into the equation the measures of the three known angles.
\(\begin{aligned} \angle 1+\angle 2+\angle 3+\angle 4&=360^{\circ} \\ 110^{\circ}+95^{\circ}+80^{\circ}+\angle 4&=360^{\circ}\end{aligned}\)
Next, simplify the left side of the equation.
\(\begin{aligned} 110^{\circ}+95^{\circ}+80^{\circ}+\angle 4&=360^{\circ} \\ 285^{\circ}+\angle 4&=360^{\circ} \end{aligned}\)
Then, subtract \(285^{\circ}\) from both sides of the equation to solve for the measure of \(\angle 4\).
\(\begin{aligned} 285^{\circ}+\angle 4 &=360^{\circ} \\ 285^{\circ}−285^{\circ}+\angle 4&=360^{\circ}−285^{\circ} \\ \angle 4&=75^{\circ} \end{aligned}\)
Example \(\PageIndex{5}\)
What is the name of the quadrilateral that has all sides equal in length, opposite sides parallel and every angle a right angle?
Solution
First, draw the quadrilateral to represent the information given in the problem.
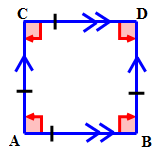
Then, name the quadrilateral.
This is a special parallelogram called a square.
Review
Use what you have learned about quadrilaterals to figure out the missing angle measure of each quadrilateral based on three given angles.
- \(120^{\circ}, 120^{\circ}, 60^{\circ}, ?\)
- \(50^{\circ}, 70^{\circ}, 130^{\circ}, ?\)
- \(52^{\circ}, 128^{\circ},52^{\circ}, ?\)
- \(47^{\circ}, 55^{\circ}, 120^{\circ}, ?\)
- \(80^{\circ}, 80^{\circ}, 100^{\circ}, ?\)
- \(105^{\circ}, 105^{\circ}, 85^{\circ}, ?\)
- \(97^{\circ}, 97^{\circ}, 35^{\circ}, ?\)
- \(120^{\circ}, 120^{\circ}, 40^{\circ}, ?\)
- \(88^{\circ}, 90^{\circ}, 60^{\circ}, ?\)
- \(25^{\circ}, 85^{\circ}, 85^{\circ}, ?\)
- \(90^{\circ}, 90^{\circ}, 90^{\circ}, ?\)
- \(140^{\circ}, 150^{\circ}, 45^{\circ}, ?\)
- \(80^{\circ}, 80^{\circ}, 120^{\circ}, ?\)
- \(75^{\circ}, 95^{\circ}, 110^{\circ}, ?\)
- \(80^{\circ}, 50^{\circ}, 95^{\circ}, ?\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 6.8.
Vocabulary
| Term | Definition |
|---|---|
| Congruent | Congruent figures are identical in size, shape and measure. |
| Parallelogram | A parallelogram is a quadrilateral with two pairs of parallel sides. |
| Quadrilateral | A quadrilateral is a closed figure with four sides and four vertices. |
| Rectangle | A rectangle is a quadrilateral with four right angles. |
| Rhombus | A rhombus is a quadrilateral with four congruent sides. |
| Square | A square is a polygon with four congruent sides and four right angles. |
| Trapezoid | A trapezoid is a quadrilateral with exactly one pair of parallel opposite sides. |
Additional Resources
Interactive Element
Video: Quadrilateral Properties
Practice: Determine Missing Angle Measures

