5.24: Congruent Polygons
- Page ID
- 5008
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Recognize and understand congruent polygons.
Congruent Figures
Chelsie wants to put a checkerboard pattern on her locker for her birthday. She has to make the pattern on poster board then tape it to her locker so that she does not permanently damage her locker. She decides that the easiest technique is to get construction paper and cut out enough squares to make her pattern. How can she tell if the squares that she cuts out are congruent?
In this concept, you will learn about congruent figures.
Congruent Figures
Congruent figures have exactly the same size and shape. They have congruent sides and congruent angles.
Here are some pairs of congruent figures.
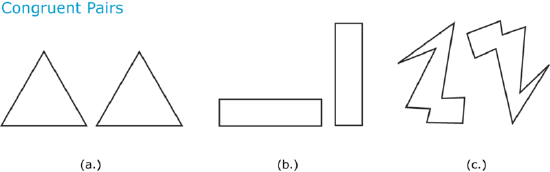
Compare the figures in each pair. They are exactly the same. If you’re not sure, imagine that you could cut out one figure and place it on top of the other. If they match exactly, they are congruent.
Test for congruency by comparing each side and angle of two figures. Each side and angle of one figure corresponds to a side or angle in the other. These are called corresponding parts. For instance, the top point of one triangle corresponds to the top point of the other triangle in a congruent pair.
It is not always easy to see the corresponding parts of two figures. One figure may be rotated differently so that the corresponding parts appear to be in different places. If you’re not sure, trace one figure and place it on top of the other to see if you can make them match.
Is the pair of figures below congruent?
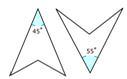
First, look at the shape of each figure.
The shapes look similar.
Next, determine if there are corresponding parts.
The given angles are not corresponding because they have different values.
Then, determine whether the shapes are corresponding.
No.
The answer is that the pair of figures are not congruent.
You can use information about one figure in a pair of congruent figures to find the measure of a corresponding angle or side in the other figure. Let’s see how this works. Take a look at the congruent figures below.
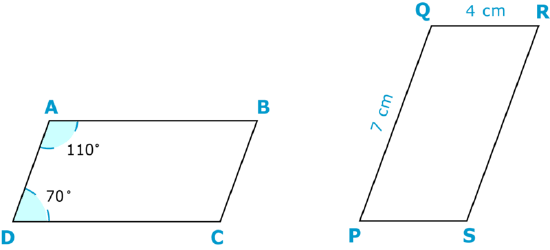
These two parallelograms are congruent. Find the corresponding parts.
First, trace one parallelogram and place it on top of the other. Rotate it until the parts correspond.
You can see that side \(AB\) corresponds to side \(PQ\) because they are congruent. Therefore,
\(AB\cong PQ\).
List all of the congruent sides.
\(\begin{aligned} AB&\cong PQ \\ BC &\cong QR \\ AD&\cong PS \\ DC &\cong SR \end{aligned}\)
List the congruent angles.
\(\begin{aligned}\angle A &\cong \angle P \qquad& \angle D&\cong \angle S \\ \angle B &\cong \angle Q \qquad& \angle C&\cong \angle R \end{aligned}\)
Now let's find the length of side \(AB\).
\(AB\) is congruent to \(PQ\), so if you find the length of \(PQ\) then it will be the same for \(AB\). \(PQ\) is 7 centimeters. Therefore AB must also be 7 centimeters long.
Now let’s look at the angles. Let's find the measure of \(\angle C\). The angle corresponds to \angle R, but you do not know the measure of \(\angle R\) either. However, you do know the measures of two of the angles in the first parallelogram: \(70^{\circ}\) and \(110^{\circ}\). You do not know the measure of \angle B, but this time you do know the measure of its corresponding angle, \(\angle Q\). These two angles are congruent, so you know that \angle B must measure \(70^{\circ}\). Now you know three of the angles in the first figure, so you can subtract to find the measure of \(\angle C\).
\(\begin{aligned} 360−(70+110+70) &=\angle C \\ 360−250&=\angle C \\ 110^{\circ}&=\angle C \end{aligned}\)
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Chelsie and her checkerboard themed locker.
She has cut out the shapes, how can she tell if the squares that she cut out are congruent?
Solution
First, measure the lengths of the sides.
All of the sides are equal.
Next, measure the angles.
All of the angles should be equal.
Then, draw a conclusion.
The shapes are congruent.
The answer is that the shapes are congruent.
Example \(\PageIndex{2}\)
Is the pair below congruent?
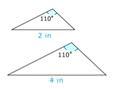
Solution
First, look at the shape of each figure.
The shapes look similar but one shape is smaller than the other.
Next, determine if there are corresponding parts.
There appears to be corresponding angles, but the sides that are in the same position are not congruent.
Then, determine if the shapes are corresponding.
No.
The answer is that the pair of figures are not congruent.
Example \(\PageIndex{3}\)
Is the pair of figures congruent?
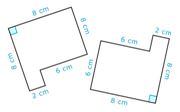
Solution
First, look at the shape of each figure.
The shapes look similar.
Next, determine if there are corresponding parts.
There appears to be corresponding angles, but not all of the sides that are in the same position are congruent.
Then, determine if the shapes are corresponding.
No.
The answer is that the pair of figures are not congruent.
Example \(\PageIndex{4}\)
What is the measure of \(\angle M\)?
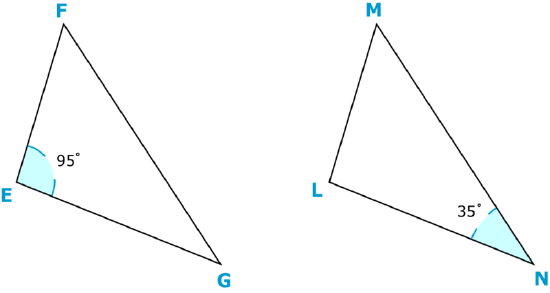Figure \(\PageIndex{7}\)Solution
First, identify the angle that corresponds with angle \(L\).
\(Angle L = Angle E = 95^{\circ}\)
Next, understand that the sum of three interior angles is 180o and write an equation.
\(95+35+x=180\)
Then, solve for the missing angle measure.
\(\begin{aligned} 130+x&=180 \\ x&=50 \end{aligned}\)
The answer is that the measure of angle M is \(50^{\circ}\).
Example \(\PageIndex{5}\)
Triangle \(DEF\) is congruent with triangle \(KLM\). If \(angle D=42^{\circ}\), what is the measure of angle \(K\)?
Solution
First, determine if angle \(K\) is congruent to angle \(D\).
Yes, it is.
Next, remember the relationship between congruent parts.
Congruent parts are equal.
Then, write the measure of angle \(K\).
\(42^{\circ}\)
The answer is that angle \(K=42^{\circ}\).
Review
Name the corresponding parts to those given below.
- \(\angle R\)
- \(MN\)
- \(\angle O\)
Use the relationships between congruent figures to find the measure of \(g\). Show your work.
-
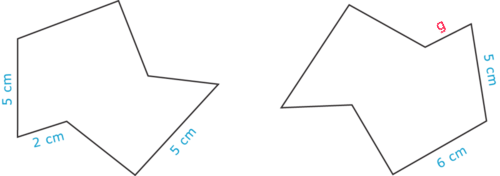
Figure \(\PageIndex{9}\)
Use the relationships between congruent figures to find the measure of \(\angle T\). Show your work.
-
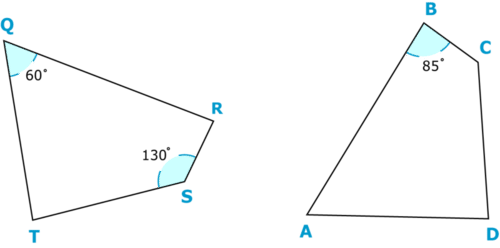
Figure \(\PageIndex{10}\)
Answer each of the following questions.
- Triangles \(ABC\) and \(DEF\) are congruent. If the measure of angle A is \(58^{\circ}\), what is the measure of angle \(D\) if it corresponds to angle \(A\)?
- True or false. Congruent figures are exactly the same in every way.
Identify the given triangles as visually congruent or not.
-
Figure \(\PageIndex{11}\) -
Figure \(\PageIndex{12}\) -
Figure \(\PageIndex{13}\) -
Figure \(\PageIndex{14}\) -
Figure \(\PageIndex{15}\)
Answer each of the following questions.
- Triangles \(ABC\) and \(DEF\) are congruent. Does this mean that their angle measures are the same? Why?
- Define Congruent.
- True or false. If two figures are congruent, then they have the same length sides but not the same angle measures.
- Triangles \(ABC\) and \(DEF\) are congruent. If the measure of angle A is \(58^{\circ}\), what is the measure of angle D if it corresponds to angle A?
Review (Answers)
To see the Review answers, open this PDF file and look for section 8.12.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Angle | A geometric figure formed by two rays that connect at a single point or vertex. |
| Congruent | Congruent figures are identical in size, shape and measure. |
| Trapezoid | A trapezoid is a quadrilateral with exactly one pair of parallel opposite sides. |
| Rigid Transformation | A rigid transformation is a transformation that preserves distance and angles, it does not change the size or shape of the figure. |
Additional Resources
Interactive Element
Video: Congruent and Similar Triangles
Practice: Congruent Polygons
Real World: Copycats