5.23: Construct Regular Polygons
- Page ID
- 5007
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Construct drawings of equilateral triangles, squares, and regular polygons using a compass and straightedge. Create polygons using Geogebra.
Constructions of Regular Polygons
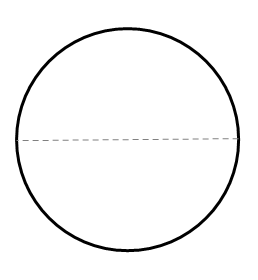
Use your compass to construct a circle like the one shown below on a piece of paper. Describe how to fold the paper two times in order to help you construct a square.

Regular Polygons
A regular polygon is a polygon that is equiangular and equilateral. This means that all its angles are the same measure and all its sides are the same length.
The most basic example of a regular polygon is an equilateral triangle, a triangle with three congruent sides and three congruent angles. Squares are also regular polygons, because all their angles are the same (\(90^{\circ}\)) and all their sides are the same length. Regular polygons with five or more sides do not have special names. Instead, the word regular is used to describe them. For example, a regular hexagon is a hexagon (6 sided polygon) whose angles are all the same measure and sides are all the same length.
All regular polygons have rotation symmetry. This means that a rotation of less than \(360^{\circ}\) will carry the regular polygon onto itself. In fact, a regular n-sided polygon has rotation symmetry for any multiple of \(\dfrac{360^{\circ}}{n}\).
Constructions are step-by-step processes used to create accurate geometric figures. To create a construction by hand, there are a few tools that you can use:
- Compass: A device that allows you to create a circle with a given radius. Not only can compasses help you to create circles, but also they can help you to copy distances.
- Straightedge: Anything that allows you to produce a straight line. A straightedge should not be able to measure distances. An index card works well as a straightedge. You can also use a ruler as a straightedge, as long as you only use it to draw straight lines and not to measure.
- Paper: When a geometric figure is on a piece of paper, the paper itself can be folded in order to construct new lines.
You can construct some regular polygons by hand if you remember the definitions and properties of these regular polygons. With the additional help of geometry software or a protractor, you can construct any regular polygon.
Let's take a look at an example problem.
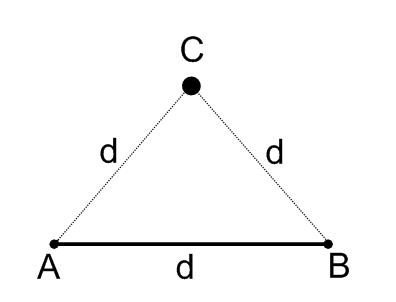
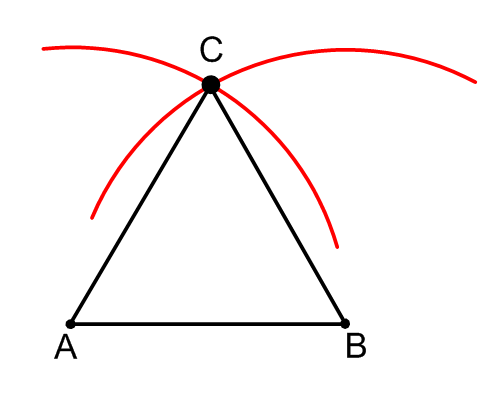
\(\overline{AB}\) is one side of what will become equilateral triangle \(\Delta ABC\). You need to put point \(C\) in the correct place in order to make the equilateral triangle. Where should point \(C\) be placed with respect to points \(A\) and \(B\)?

Let the distance between \(A\) and \(B\) be \(d\). Point \(C\) needs to be d away from point \(A\) and also \(d\) away from point \(B\).
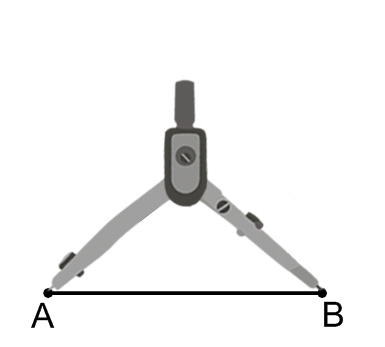
Use a straightedge to draw line segment \(\overline{AB}\). Use the ideas from Example A to construct equilateral triangle \(\Delta ABC\).

Use a compass to measure the length of \(\overline{AB}\).
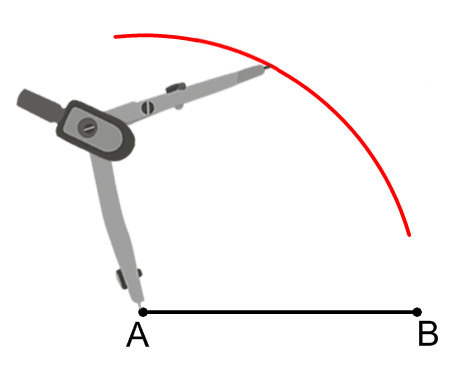
Make a partial circle of points that are the length of \(\overline{AB}\) away from point \(A\).
Make another partial circle of points that are the length of \(\overline{AB}\) away from point \(B\).
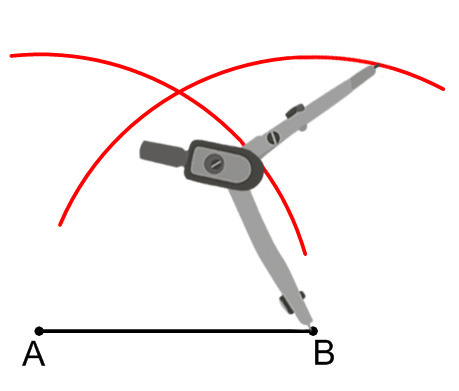
The point of intersection of these two partial circles is point \(C\).
Points \(A\), \(B\), \(C\), and \(D\) are on a circle centered at point \(O\). Prove that \(ABCD\) is a square.
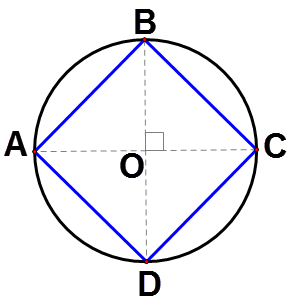
\(\overline{AO}\cong \overline{BO}\cong \overline{CO}\cong \overline{DO}\) because they are all radii of the same circle. Since\(\angle BOC\) is a right angle, \(\angle BOA\),\angle AOD\) and \(\angle COD\) must also be right angles. Therefore, \(\angle BOC\cong \angle BOA\cong \angle AOD\cong \angle COD\). This means that \(\Delta BOC\cong \Delta AOB\cong \Delta DOA\cong \Delta COD\) by SAS\cong\). \(\overline{AB}\cong \overline{BC}\cong \overline{CD}\cong \overline{DA}\) because they are corresponding parts of congruent triangles.
All four triangles are isosceles because they each have two congruent sides. This means that their base angles are congruent. Because the vertex angle of each triangle is \(90^{\circ}\), the base angles of each triangle must be \(45^{\circ} (90+45+45=180)\). The four angles that make up the quadrilateral are each made of two of these \(45^{\circ}\) angles, and are each therefore \(90^{\circ}\).
Because the quadrilateral has four congruent sides and four \(90^{\circ}\) angles, it is a square.
Example \(\PageIndex{1}\)
Earlier, you were asked to describe how to fold the paper two times in order to help you construct a square.
Solution
Fold the circle so that the two halves overlap to create a crease that is the diameter.
Fold the circle in half again to create the perpendicular bisector of the diameter. To do this, fold so that the two endpoints of the diameter meet. The second crease will also be a diameter.
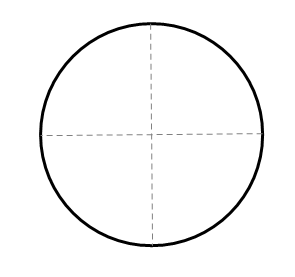
Note that the two diameters are perpendicular to one another. Connect the four points of intersection on the circle to construct the square.
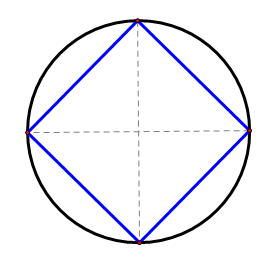
You can be certain that this is a square due to the proof in Example C.
Example \(\PageIndex{2}\)
The regular hexagon below has been divided into six congruent triangles. What type of triangles are they? Explain.
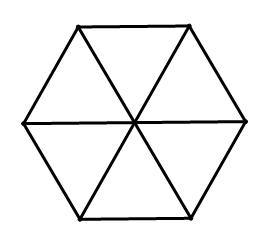
Solution
They must be equilateral triangles.
- A full circle is \(360^{\circ}\), so each angle at the center of the hexagon must be \(\dfrac{360^{\circ} }{6}=60^{\circ}\). *This is also why regular hexagons demonstrate rotation symmetry at multiples of \(60^{\circ}\).*
- The six triangles are congruent, so the six segments connecting the center of the hexagon to the vertices must be congruent. This means the six triangles are all isosceles.
- The base angles of each of the isosceles triangles must be \(\dfrac{180−60}{2}=60^{\circ}\).
- The measure of each angle of all of the triangles is \(60^{\circ}\), so all triangles are equilateral.
Example \(\PageIndex{3}\)
Six points have been evenly spaced around the circle below. Explain why a regular hexagon is created when these points are connected.
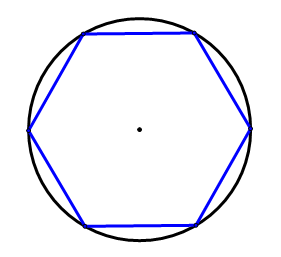
Solution
Because the six points are evenly spaced, each of the segments connecting the six points must be the same length. Therefore, the polygon must be regular. Because there are six sides, it must be a regular hexagon.
Example \(\PageIndex{4}\)
Construct a regular hexagon inscribed in a circle.
Solution
“Inscribed in a circle” means all six vertices of the hexagon are on the same circle. Start by constructing a circle and a point on the circle.

You know that the radius of the circle is the same as the length of each side of the circle (see guided practice #1). Therefore, your goal is to place six points around the circle that are the same distance apart from one another as the radius of the circle. Keep your compass open to the same width as the radius of the circle and make one new mark on the circle.

Continue to make new marks around the circle that are the same distance apart from one another.

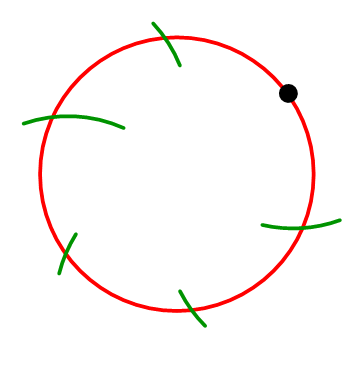
Connect the intersection points to form the regular hexagon.

Review
1. Construct an equilateral triangle.
2. Construct another equilateral triangle.
3. Explain why your process for constructing equilateral triangles works.
4. Construct a square inscribed in a circle by making two folds.
5. Justify why the polygon you've created is actually a square.
Use your straightedge to construct \(\overline{AB}\).
6. Construct the perpendicular bisector of \(\overline{AB}\).
7. Construct a circle with diameter \(\overline{AB}\).
8. Construct a square inscribed in the circle by connecting the four endpoints of the diameters.
9. Extend your construction to a regular octagon by bisecting each of the right angles at the center of the circle.
10. Construct a regular hexagon inscribed in a circle.
11. Explain why the method for constructing a regular hexagon relies on a circle.
12. Explain how you could extend your construction of the regular hexagon to a construction of a regular 12-gon.
13. Construct an equilateral triangle. Explain how you could construct the circle that passes through the three points of the equilateral triangle.
14. Given an equilateral triangle inscribed in a circle, how could you extend the construction to construct a regular hexagon?
15. Given a circle and a protractor, explain how you could create a regular pentagon.
Review (Answers)
To see the Review answers, open this PDF file and look for section 5.4.
Vocabulary
| Term | Definition |
|---|---|
| Regular Polygon | A regular polygon is a polygon with all sides the same length and all angles the same measure. |
| Equilateral | A polygon is equilateral if all of its sides are the same length. |
| Equiangular | A polygon is equiangular if all angles are the same measure. |

