5.28: Exterior Angles in Convex Polygons
- Page ID
- 5013
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Measure of angles on the outside of a polygon formed by extending a side.
Exterior Angle Sum Theorem
An exterior angle is an angle that is formed by extending a side of the polygon.
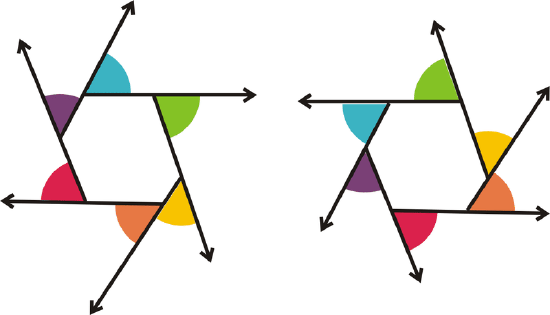
As you can see, there are two sets of exterior angles for any vertex on a polygon, one going around clockwise (1st hexagon), and the other going around counter-clockwise (2nd hexagon). The angles with the same colors are vertical and congruent.
The Exterior Angle Sum Theorem states that the sum of the exterior angles of ANY convex polygon is \(360^{\circ}\). If the polygon is regular with n sides, this means that each exterior angle is \(\dfrac{360^{\circ}}{n}\).
What if you were given a seven-sided regular polygon? How could you determine the measure of each of its exterior angles?
Example \(\PageIndex{1}\)
What is the measure of each exterior angle of a regular 12-gon?
Solution
Divide \(360^{\circ}\) by the given number of sides.
\(30^{\circ}\)
Example \(\PageIndex{2}\)
What is the measure of each exterior angle of a regular 100-gon?
Solution
Divide \(360^{\circ}\) by the given number of sides.
\(3.6^{\circ}\)
Example \(\PageIndex{3}\)
What is y?
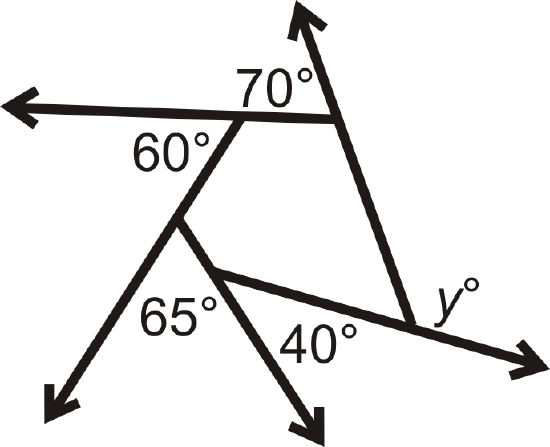
Solution
\(y\) is an exterior angle and all the given angles add up to \(360^{\circ}\). Set up an equation.
\(\begin{aligned} 70^{\circ}+60^{\circ}+65^{\circ}+40^{\circ}+y&=360^{\circ} \\ y&=125^{\circ} \end{aligned}\)
Example \(\PageIndex{4}\)
What is the measure of each exterior angle of a regular heptagon?
Solution
Because the polygon is regular, the interior angles are equal. It also means the exterior angles are equal. \(\dfrac{360^{\circ}}{7}\approx 51.43^{\circ}\)
Example \(\PageIndex{5}\)
What is the sum of the exterior angles in a regular 15-gon?
Solution
The sum of the exterior angles in any convex polygon, including a regular 15-gon, is \(360^{\circ}\).
Review
- What is the measure of each exterior angle of a regular decagon?
- What is the measure of each exterior angle of a regular 30-gon?
- What is the sum of the exterior angles of a regular 27-gon?
Find the measure of the missing variables:
-
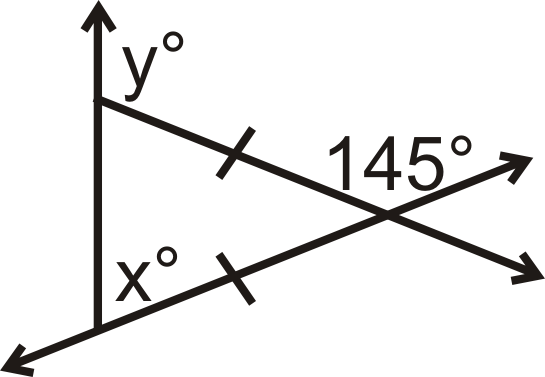
Figure \(\PageIndex{3}\) -
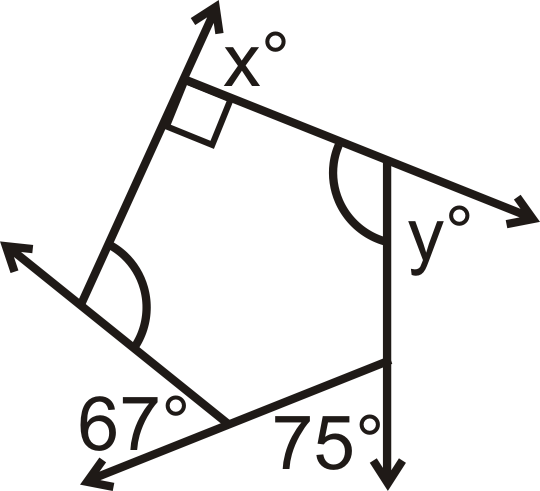
Figure \(\PageIndex{4}\)
- The exterior angles of a quadrilateral are \(x^{\circ}\), \(2x^{\circ}\), \(3x^{\circ}\), and \(4x^{\circ}\). What is \(x\)?
Find the measure of each exterior angle for each regular polygon below:
- octagon
- nonagon
- triangle
- pentagon
Review (Answers)
To see the Review answers, open this PDF file and look for section 6.2.
Resources
Vocabulary
| Term | Definition |
|---|---|
| exterior angle | An angle that is formed by extending a side of the polygon. |
| regular polygon | A polygon in which all of its sides and all of its angles are congruent. |
| Exterior Angle Sum Theorem | Exterior Angle Sum Theorem states that the exterior angles of any polygon will always add up to 360 degrees. |
Additional Resources
Interactive Element
Video: Interior and Exterior Angles of a Polygon
Activities: Exterior Angles in Convex Polygons Discussion Questions
Study Aids: Polygons Study Guide
Real World: Exterior Angles Theorem