5.7: Quadrilateral Classification
- Page ID
- 4991
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Categorize quadrilaterals based on sides and angles. Identify them visually, and by description. Find lengths and angles, determine shapes, and prove congruence and if lines are parallel.

Rasha is helping her father paint the door frame of their home. She calls out the names of each shape that she paints. She reaches a shape that she cannot name. She sees that it has four sides and one set of parallel sides. What shape is she painting?
In this concept, you will learn how to identify and classify quadrilaterals.
Classifying Quadrilaterals
Polygons are closed shapes with sides made up of lines. Any closed shape with straight edges, such as a triangle or rectangle, is a polygon.
Polygons with four sides, such as rectangles and squares, are called quadrilaterals. The prefix of this word “quad” means four, therefore, a quadrilateral is a polygon that has four sides. Quadrilaterals also have four angles, and these four angles have a sum of 360∘. This is true for all quadrilaterals
Another important feature of quadrilaterals is that many have one or even two pairs of parallel sides. Look at the quadrilaterals below.
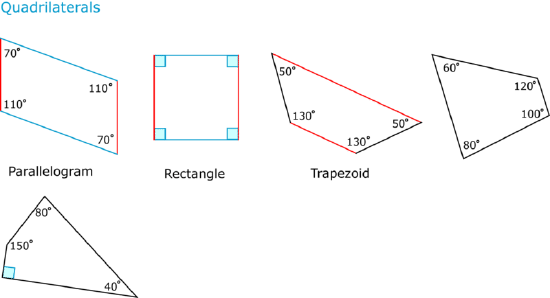
Let’s look at the different types of quadrilaterals in detail.
A parallelogram is a quadrilateral with opposite sides parallel. The first figure above is a parallelogram. There are a few special features of parallelograms. One is that each pair of parallel sides is congruent. In the first figure above, the two short sides are the same length and the two long sides are the same length. This special relationship between the pairs of sides affects the angles of a parallelogram: the angles opposite each other are congruent. The 70∘ angles are opposite each other, and the 110∘ angles are opposite each other. This relationship exists in any parallelogram, no matter the length of the sides or the sizes of the angle pairs.
There are three special kinds of parallelograms.
A rectangle is a quadrilateral because it has four sides, and it is a parallelogram because it has two pairs of parallel, congruent sides. All four angles are right angles.
A square has two pairs of parallel sides and four right angles. All four of its sides are congruent.
The third special parallelogram is called a rhombus. Like a square, a rhombus has four congruent sides and pairs of congruent angles opposite each other. However, right angles are not required for a rhombus. So a rhombus canbe a square, but a square isn’t necessarily a rhombus because of the right angles necessary in a square.
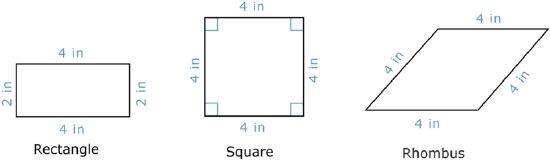
Let’s look at an example.
Identify the shape below as a rectangle, square, rhombus, or just a parallelogram.
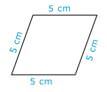
First, check the lengths of the sides.
The shape has four sides of equal lengths.
Next, check to see if the shape has four right angles.
The shape does not have four right angles.
Then, identify the shape.
Rhombus.
The answer is a rhombus.
Now let’s look at one other special quadrilateral.
A trapezoid is a quadrilateral that has only one pair of parallel sides.
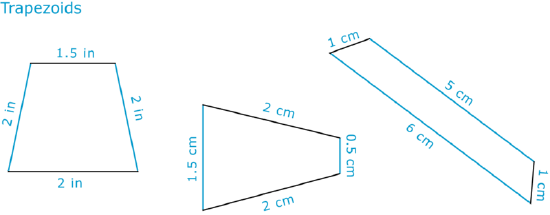
Example \(\PageIndex{1}\)
Earlier, you were given a problem about Rasha and the door frame of her home.
She paints a shape that has four sides and one set of parallel sides. What shape is she painting?
Solution
First, check the number of sides.
The shape has four sides.
Next, check to see if the shape has parallel sides.
The shape has one set of parallel sides.
Then, identify the shape.
Trapezoid.
The answer is that Rasha is painting a trapezoid.
Example \(\PageIndex{2}\)
Identify the shape below as a rectangle, square, rhombus, or parallelogram.
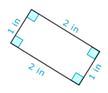
Solution
First, check the lengths of the sides.
The opposite sides are congruent.
Next, check to see if the shape has four right angles.
The shape has four right angles.
Then, identify the shape.
Rectangle.
The answer is rectangle.
Example \(\PageIndex{3}\)
Identify each type of quadrilateral based on its description.
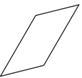
Solution
First, check the lengths of the sides.
The length of the sides is unknown, but the opposite sides appear to be congruent.
Next, check to see if the shape has four right angles.
The shape does not have four right angles.
Then, identify the shape.
Parallelogram.
The answer is parallelogram.
Example \(\PageIndex{4}\)
A four sided figure with opposite sides parallel and congruent with four right angles.
Solution
First, check the number of sides.
The shape has four sides.
Next, note the relationship between the opposite sides.
The opposite sides are parallel and congruent.
Then, classify the shape.
Square.
The answer is a square.
Example \(\PageIndex{5}\)
A four sided figure with two pairs of parallel sides. Opposite sides are congruent.
Solution
First, check the number of sides.
The shape has four sides.
Next, note the relationship between the opposite sides.
The opposite sides are parallel and the parallel sides are congruent.
Then, classify the shape.
Parallelogram.
The answer is a parallelogram.
Review
Identify each quadrilateral as a parallelogram, rectangle, square, rhombus, or trapezoid.
-

Figure \(\PageIndex{8}\) -

Figure \(\PageIndex{9}\) -

Figure \(\PageIndex{10}\) -

Figure \(\PageIndex{11}\)
Look at each image and name the quadrilateral pictured.
-

Figure \(\PageIndex{12}\) -

Figure \(\PageIndex{13}\) -

Figure \(\PageIndex{14}\) -

Figure \(\PageIndex{15}\) -

Figure \(\PageIndex{16}\)
Name the geometric figure described below or answer each question.
- Has four sides and four angles
- Has one pair of opposite sides that are parallel
- Has four right angles and four congruent sides
- A parallelogram with four right angles.
- A parallelogram with four congruent sides
- Has four right angles and opposite sides congruent
Resources
Vocabulary
| Term | Definition |
|---|---|
| Kite | A kite is a quadrilateral with distinct adjacent congruent sides. |
| Parallelogram | A parallelogram is a quadrilateral with two pairs of parallel sides. |
| Polygon | A polygon is a simple closed figure with at least three straight sides. |
| Quadrilateral | A quadrilateral is a closed figure with four sides and four vertices. |
| Rectangle | A rectangle is a quadrilateral with four right angles. |
| Rhombus | A rhombus is a quadrilateral with four congruent sides. |
| Trapezoid | A trapezoid is a quadrilateral with exactly one pair of parallel opposite sides. |
Additional Resources
Interactive Element
Video: Quadrilateral Properties
Activities: Quadrilateral Classification Discussion Questions
Study Aids: Parallelograms Study Guide
Practice: Quadrilateral Classification
Real World: Quadrilateral Classification

