5.8: Parallelogram Classification
- Page ID
- 4992
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Rectangles, rhombuses, and squares are parallelograms defined by their diagonals, angles, and sides.
Classifying Parallelograms
Rectangles, rhombuses (also called rhombi) and squares are all more specific versions of parallelograms, also called special parallelograms.
- A quadrilateral is a rectangle if and only if it has four right (congruent) angles.
\(ABCD\) is a rectangle if and only if \(\angle A\cong \angle B\cong \angle C\cong \angle D\).
- A quadrilateral is a rhombus if and only if it has four congruent sides.
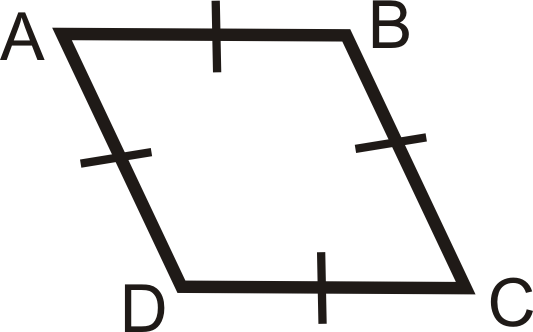
\(ABCD\) is a rhombus if and only if \(\overline{AB}\cong \overline{BC} \cong \overline{CD} \cong \overline{AD}\).
- A quadrilateral is a square if and only if it has four right angles and four congruent sides. By definition, a square is a rectangle and a rhombus.
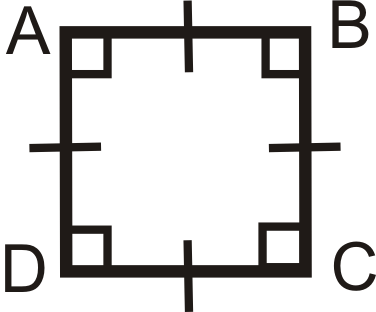
\(ABCD\) is a square if and only if \(\angle A\cong \angle B\cong \angle C\cong \angle D\) and \(\overline{AB}\cong \overline{BC} \cong \overline{CD} \cong \overline{AD}\).
You can always show that a parallelogram is a rectangle, rhombus, or square by using the definitions of these shapes. There are some additional ways to prove parallelograms are rectangles and rhombuses, shown below:
1. A parallelogram is a rectangle if the diagonals are congruent.
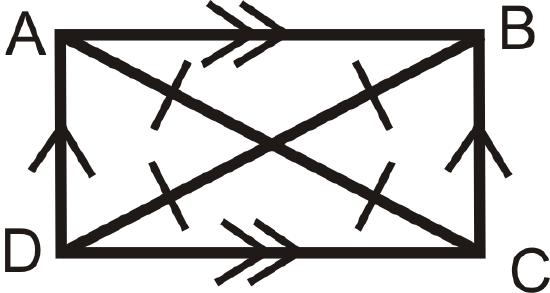
\(ABCD\) is parallelogram. If \(\overline{AC}\cong \overline{BD}\), then \(ABCD\) is also a rectangle.
2. A parallelogram is a rhombus if the diagonals are perpendicular.
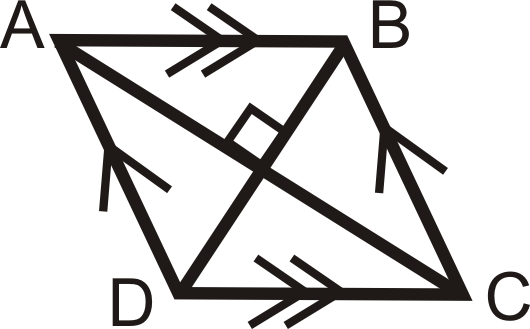
\(ABCD\) is a parallelogram. If \(\overline{AC}\perp \overline{BD}\), then \(ABCD\) is also a rhombus.
3. A parallelogram is a rhombus if the diagonals bisect each angle.
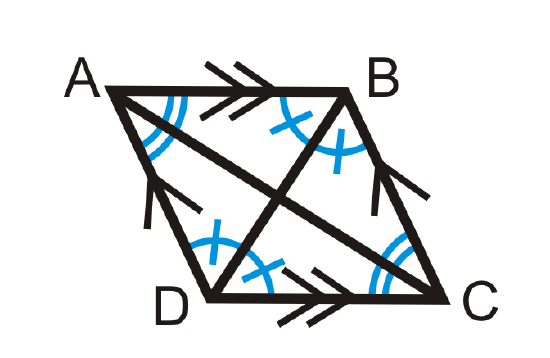
\(ABCD\) is a parallelogram. If \(\overline{AC}\) bisects \(\angle BAD\) and \(\angle BCD\) and \(\overline{BD}\) bisects \(\angle ABC\) and \(\angle ADC\), then \(ABCD\) is also a rhombus.
What if you were given a parallelogram and information about its diagonals? How could you use that information to classify the parallelogram as a rectangle, rhombus, and/or square?
Example \(\PageIndex{1}\)
Is a rectangle SOMETIMES, ALWAYS, or NEVER a parallelogram? Explain why.
Solution
A rectangle has two sets of parallel sides, so it is ALWAYS a parallelogram.
Example \(\PageIndex{2}\)
Is a quadrilateral SOMETIMES, ALWAYS, or NEVER a pentagon? Explain why.
Solution
A quadrilateral has four sides, so it will NEVER be a pentagon with five sides.
Example \(\PageIndex{3}\)
What typed of parallelogram are the figures below?
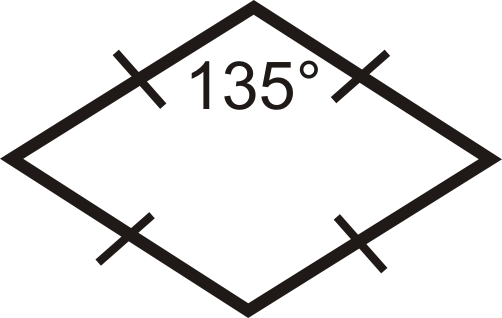
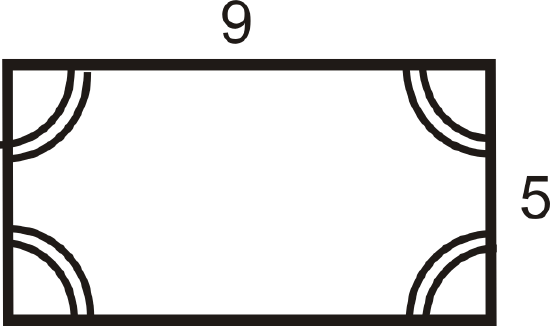
Solution
For the first figure, all sides are congruent and one angle is \(135^{\circ}\), so the angles are not congruent. This is a rhombus.
For the second figure, all four angles are congruent but the sides are not. This is a rectangle.
Example \(\PageIndex{4}\)
Is a rhombus SOMETIMES, ALWAYS, or NEVER a square? Explain why.
Solution
A rhombus has four congruent sides and a square has four congruent sides and angles. Therefore, a rhombus is a square when it has congruent angles. This means a rhombus is SOMETIMES a square.
Example \(\PageIndex{5}\)
List everything you know about the square \(SQRE\).
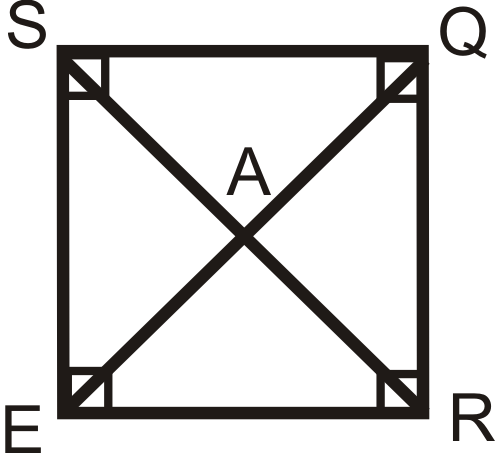
Solution
A square has all the properties of a parallelogram, rectangle and rhombus.
| Properties of a Parallelogram | Properties of a Rhombus | Properties of a Rectangle |
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
All the bisected angles are \(45^{\circ}\).
Review
- \(RACE\) is a rectangle. Find:
- \(RG\)
- \(AE\)
- \(AC\)
- \(EC\)
- \(m\angle RAC\)
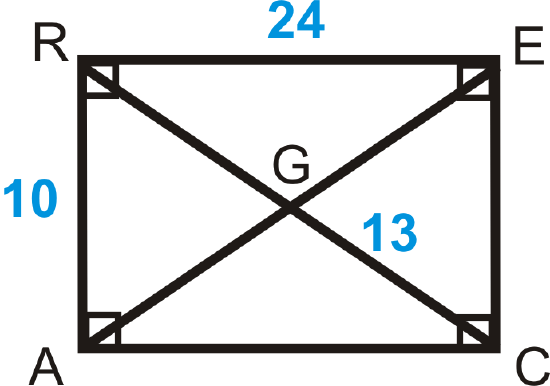Figure \(\PageIndex{10}\) - \(DIAM\) is a rhombus. Find:
- \(MA\)
- \(MI\)
- \(DA\)
- \(m\angle DIA\)
- \(m\angle MOA\)
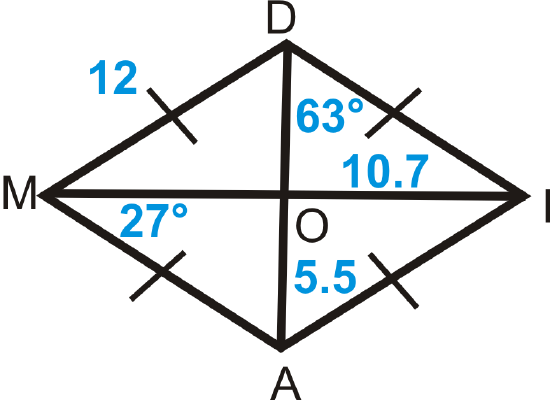Figure \(\PageIndex{11}\) - \(CUBE\) is a square. Find:
- \(m\angle UCE\)
- \(m\angle EYB\)
- \(m\angle UBY\)
- \(m\angle UEB\)
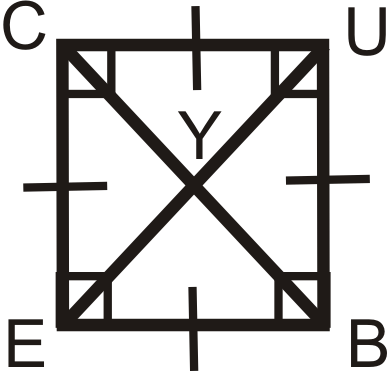
Figure \(\PageIndex{12}\)
For questions 4-15, determine if the quadrilateral is a parallelogram, rectangle, rhombus, square or none.
-
Figure \(\PageIndex{13}\) -
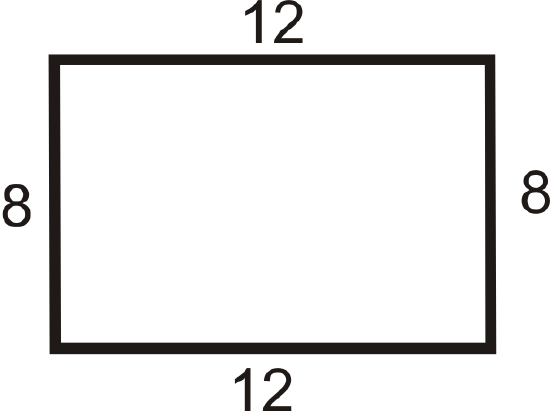
Figure \(\PageIndex{14}\) -
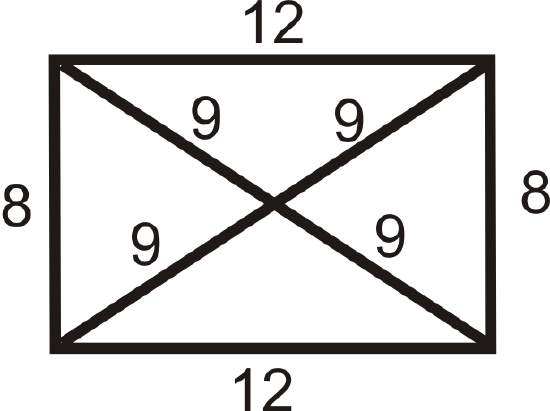
Figure \(\PageIndex{15}\) -
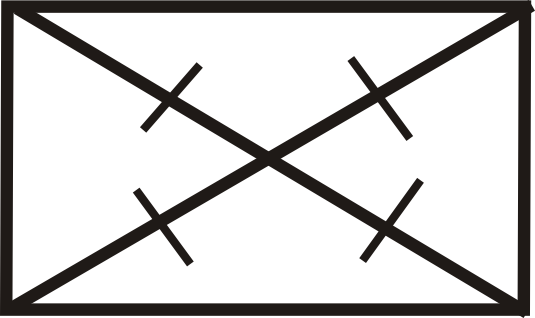
Figure \(\PageIndex{16}\) -
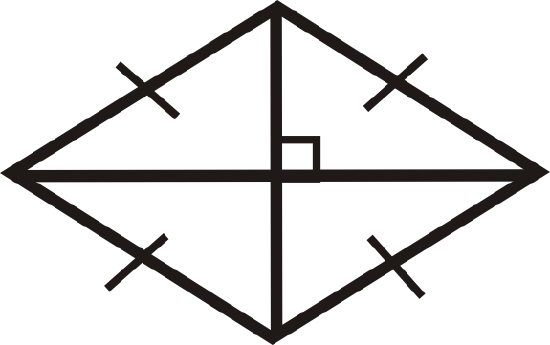
Figure \(\PageIndex{17}\) -
Figure \(\PageIndex{18}\) -
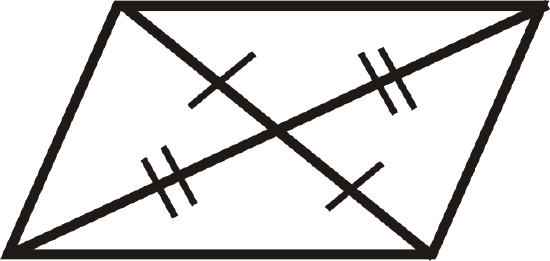
Figure \(\PageIndex{19}\) -
Figure \(\PageIndex{20}\) -
Figure \(\PageIndex{21}\) -
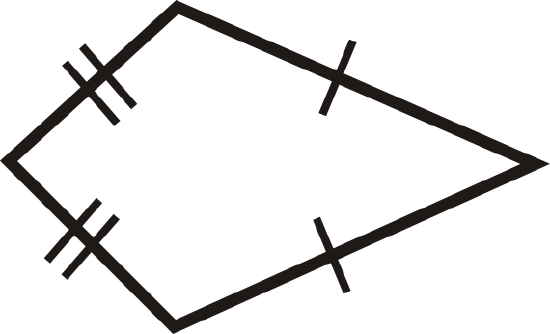
Figure \(\PageIndex{22}\) -
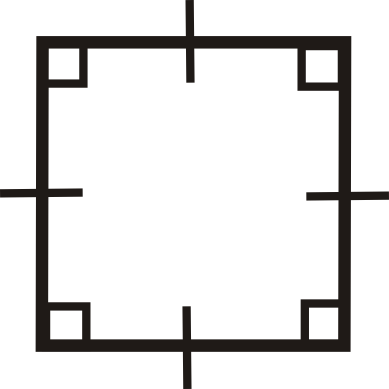
Figure \(\PageIndex{23}\) -
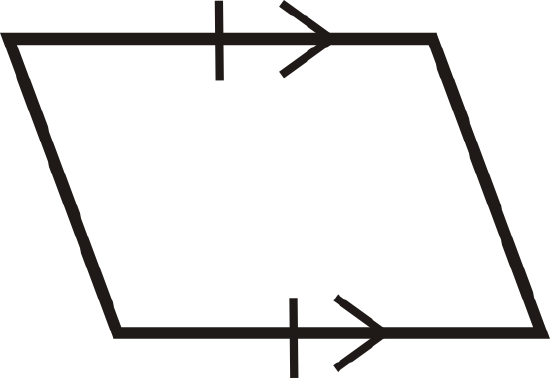
Figure \(\PageIndex{24}\)
For questions 16-19 determine if the following are ALWAYS, SOMETIME, or NEVER true. Explain your reasoning.
- A rectangle is a rhombus.
- A square is a parallelogram.
- A parallelogram is regular.
- A square is a rectangle.
Review (Answers)
To see the Review answers, open this PDF file and look for section 6.5.
Vocabulary
| Term | Definition |
|---|---|
| rectangle | A parallelogram is a rectangle if and only if it has four right (congruent) angles |
| rhombus | A parallelogram is a rhombus if and only if it has four congruent sides |
| square | A parallelogram is a square if and only if it has four right angles and four congruent sides. |
| converse | If a conditional statement is \(p\rightarrow q\) (if \(p\), then \(q\)), then the converse is \(q\rightarrow p\) (if \(q\), then \(p\). Note that the converse of a statement is not true just because the original statement is true. |
| Parallelogram | A parallelogram is a quadrilateral with two pairs of parallel sides. |
| Reflexive Property of Congruence | \(\overline{AB}\cong \overline{AB}\) or \(\angle B\cong \angle B\) |
Additional Resources
Interactive Element
Video: Classifying Parallelograms Principles - Basic
Activities: Parallelogram Classification Discussion Questions
Study Aids: Parallelograms Study Guide
Practice: Parallelogram Classification
Real World: Parallelograms