6.20: Tangent Secant Theorem
- Page ID
- 5045
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Product of the outside segment and whole secant equals the square of the tangent to the same point.
Segments from Secants and Tangents
If a tangent and secant meet at a common point outside a circle, the segments created have a similar relationship to that of two secant rays.
Tangent Secant Segment Theorem: If a tangent and a secant are drawn from a common point outside the circle (and the segments are labeled like the picture below), then \(a^2=b(b+c)\).
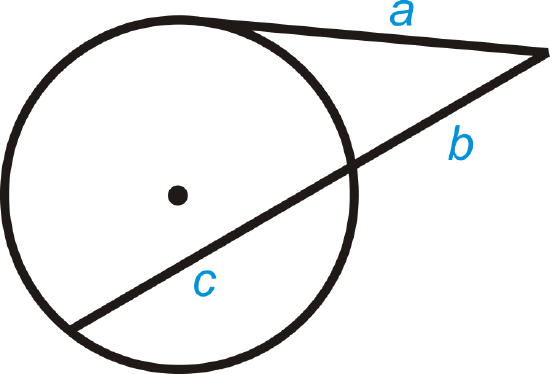
What if you were given a circle with a tangent and a secant that intersect outside the circle? How could you use the length of some of the segments formed by their intersection to determine the lengths of the unknown segments?
Example \(\PageIndex{1}\)
Find \(x\). Simplify any radicals.
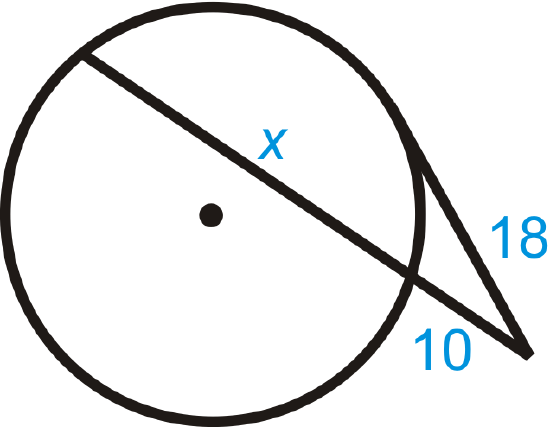
Solution
Use the Tangent Secant Segment Theorem.
\(\begin{aligned} 18^2&=10(10+x) \\ 324&=100+10x \\ 224&=10x \\ x&=22.4\end{aligned}\)
Example \(\PageIndex{2}\)
Find \(x\). Simplify any radicals.
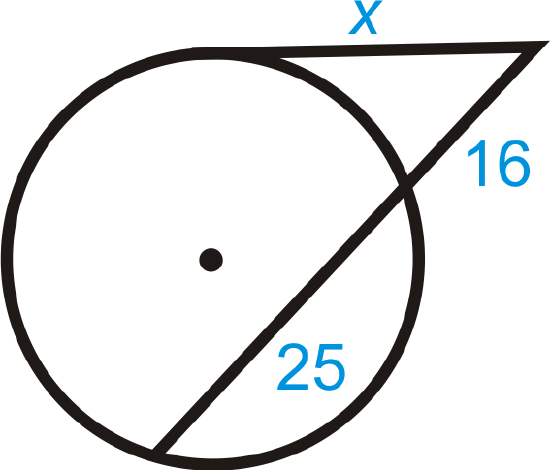
Solution
Use the Tangent Secant Segment Theorem.
\(\begin{aligned} x^2&=16(16+25) \\ x^2&=656 \\ x&=4\sqrt{41}\end{aligned}\)
Example \(\PageIndex{3}\)
Find the length of the missing segment.
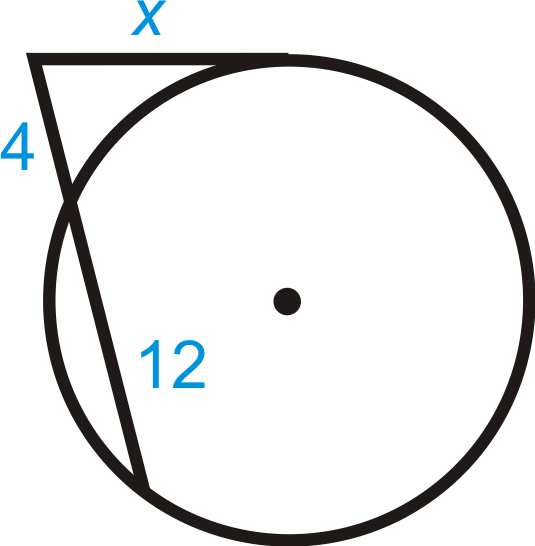
Solution
Use the Tangent Secant Segment Theorem.
\(\begin{aligned} x^2&=4(4+12) \\ x^2&=4\cdot 16=64 \\ x&=8\end{aligned}\)
Example \(\PageIndex{4}\)
Fill in the blank and then solve for the missing segment.
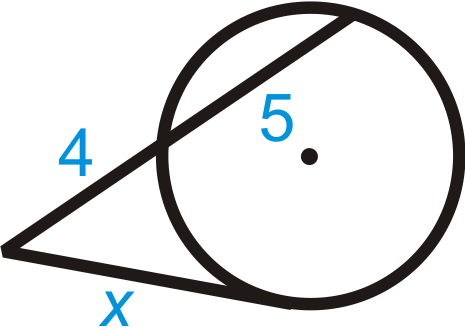
Solution
\(\text{______}=\text{______}(4+5)\)
\(\begin{aligned} x^2&=4(4+5) \\ x^2&=36 \\ x&=6\end{aligned}\)
Example \(\PageIndex{5}\)
Find the value of the missing segment.
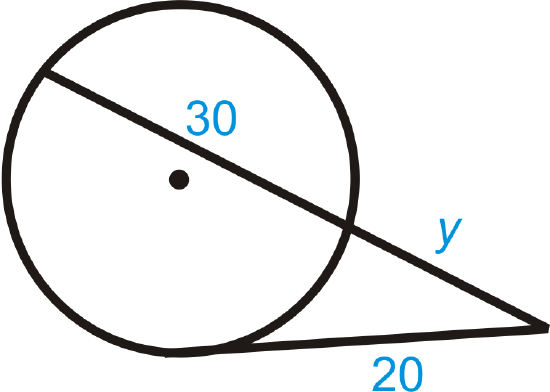
Solution
Use the Tangent Secant Segment Theorem.
\(\begin{aligned} 20^2&=y(y+30) \\ 400&=y^2+30y \\ 0&=y^2+30y−400 \\ 0&=(y+40)(y−10) \\ y&=\xcancel{−40},10 \end{aligned}\)
Review
Fill in the blanks for each problem below and then solve for the missing segment.
-
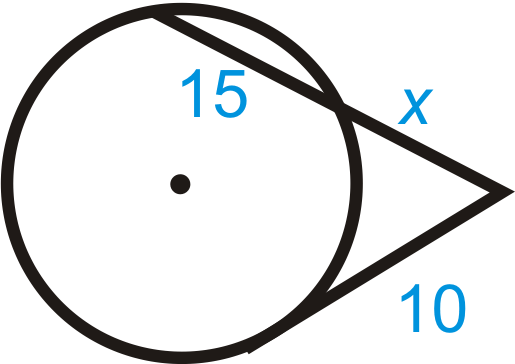
Figure \(\PageIndex{7}\)
\(10^2=x(\text{______}+\text{______})\)
Find \(x\) in each diagram below. Simplify any radicals.
-
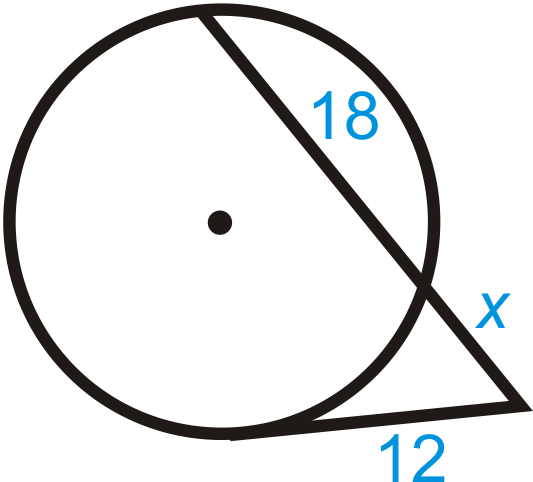
Figure \(\PageIndex{8}\) -
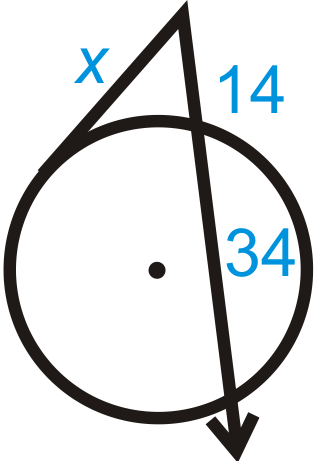
Figure \(\PageIndex{9}\) -
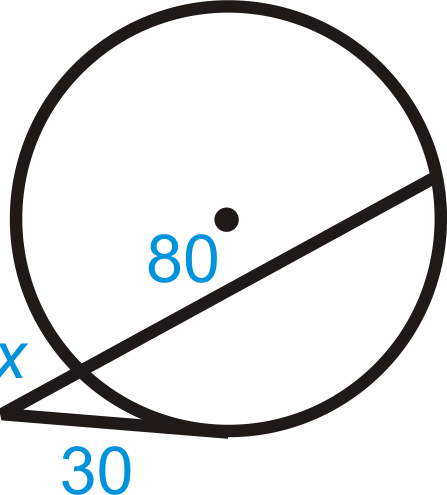
Figure \(\PageIndex{10}\) - Describe and correct the error in finding \(y\).
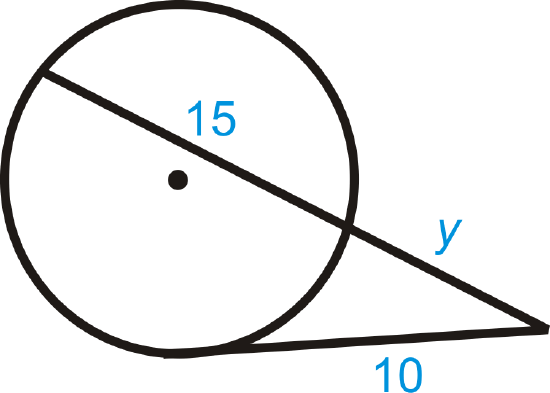
Figure \(\PageIndex{11}\)
\(\begin{aligned} 10\cdot 10&=y\cdot 15y \\ 100&=15y^2 \\ \dfrac{20}{3}&=y^2 \\ \dfrac{2\sqrt{15}}{3}&=y \color{red} \leftarrow \text{y is \underline{not} correct}\end{aligned}\)
Solve for the unknown variable.
-
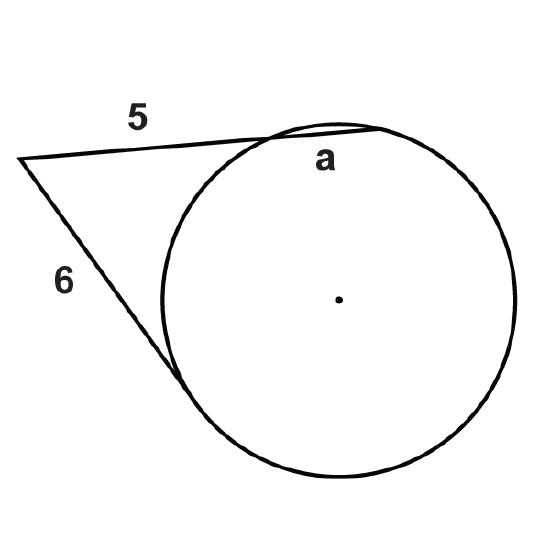
Figure \(\PageIndex{12}\) -
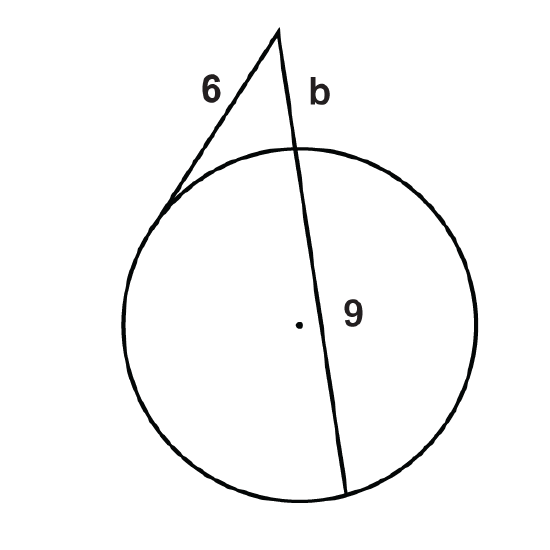
Figure \(\PageIndex{13}\) -
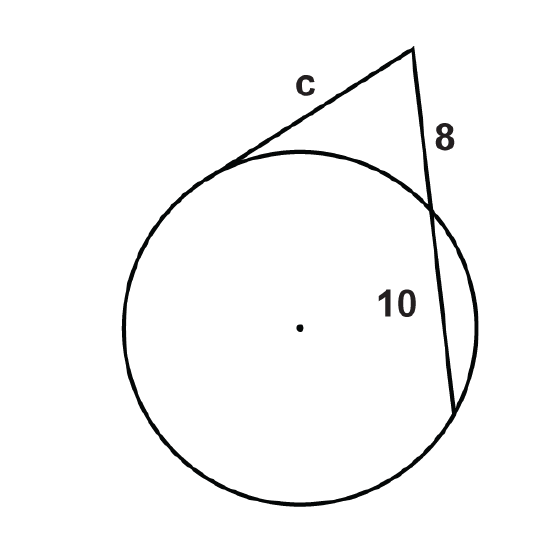
Figure \(\PageIndex{14}\) -
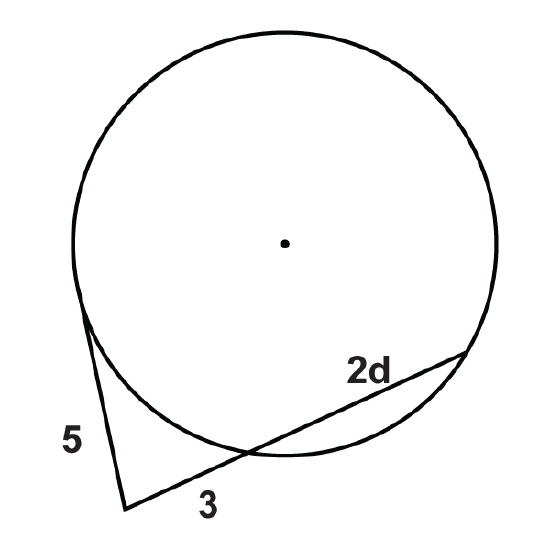
Figure \(\PageIndex{15}\) -
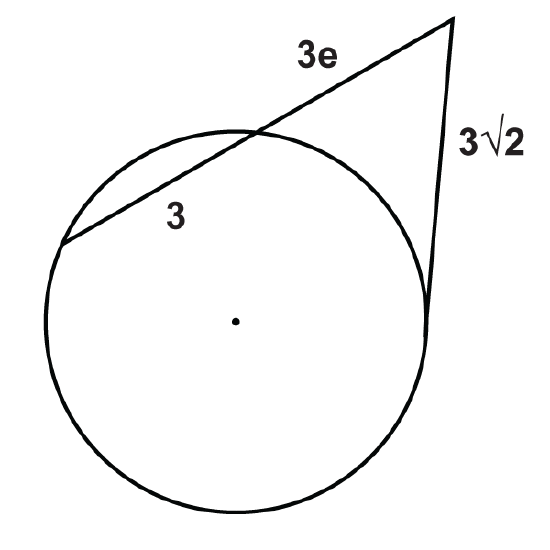
Figure \(\PageIndex{16}\) -
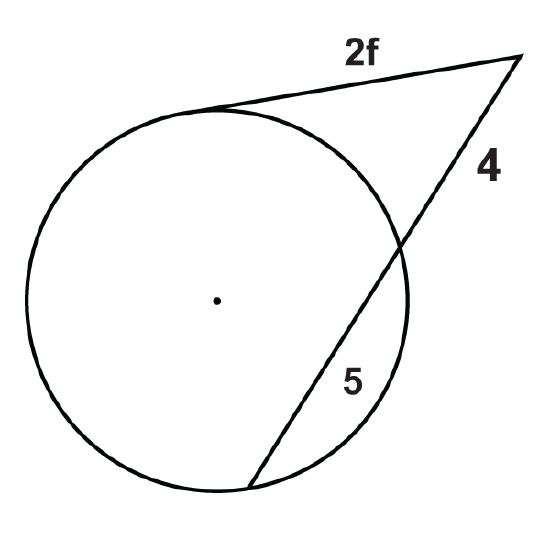
Figure \(\PageIndex{17}\) -
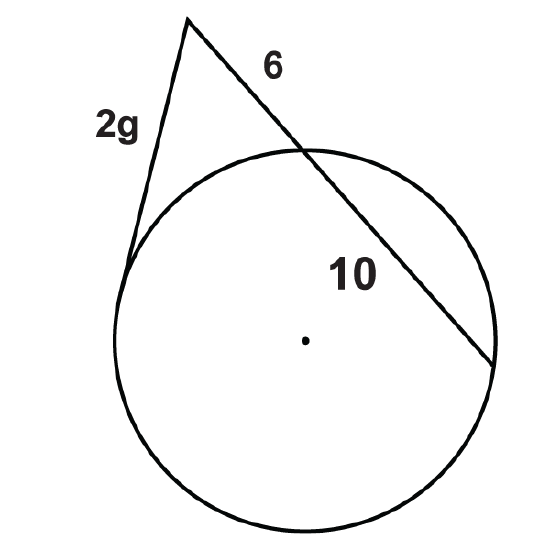
Figure \(\PageIndex{18}\) -
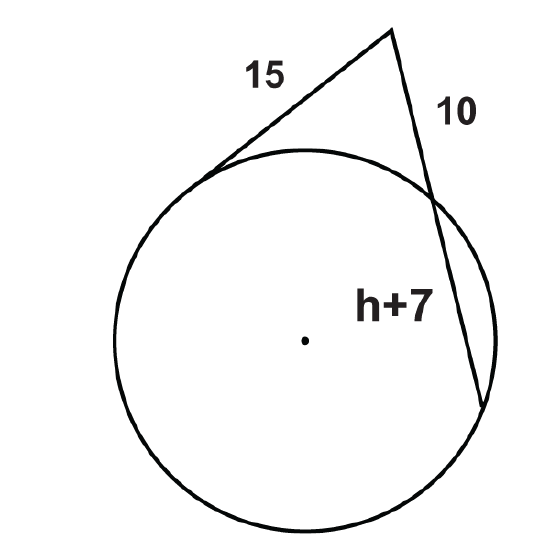
Figure \(\PageIndex{19}\) -
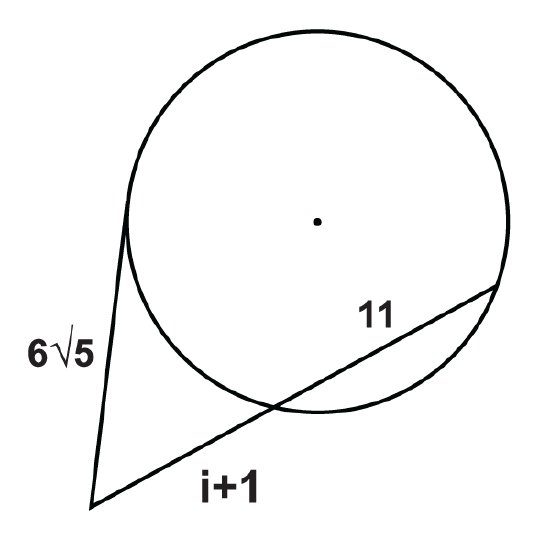
Figure \(\PageIndex{20}\) -
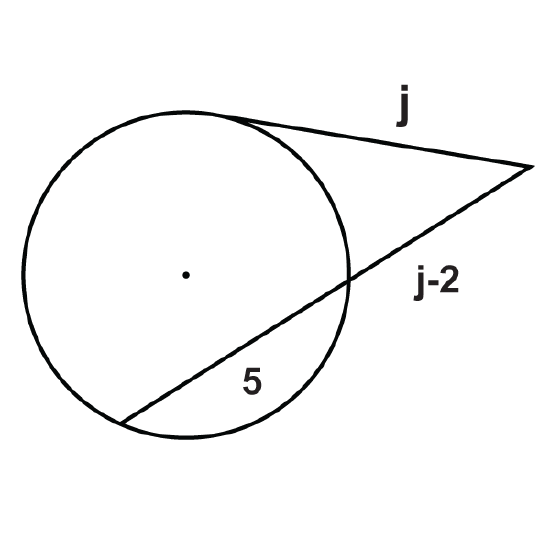
Figure \(\PageIndex{21}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 9.11.
Vocabulary
| Term | Definition |
|---|---|
| central angle | An angle formed by two radii and whose vertex is at the center of the circle. |
| chord | A line segment whose endpoints are on a circle. |
| circle | The set of all points that are the same distance away from a specific point, called the center. |
| diameter | A chord that passes through the center of the circle. The length of a diameter is two times the length of a radius. |
| inscribed angle | An angle with its vertex on the circle and whose sides are chords. |
| intercepted arc | The arc that is inside an inscribed angle and whose endpoints are on the angle. |
| point of tangency | The point where the tangent line touches the circle. |
| radius | The distance from the center to the outer rim of a circle. |
| Secant | The secant of an angle in a right triangle is the value found by dividing length of the hypotenuse by the length of the side adjacent the given angle. The secant ratio is the reciprocal of the cosine ratio. |
| Tangents Secant Segments Theorem | If a tangent and a secant are drawn from a common point outside the circle (and the segments are labeled like the picture below), then \(a^2 = b(b+c)\). |
Additional Resources
Interactive Element
Activities: Segments from Secants and Tangents Discussion Questions
Study Aids: Circles: Segments and Lengths Study Guide
Practice: Tangent Secant Theorem

