6.21: Circles in the Coordinate Plane
- Page ID
- 5046
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Graph a circle. Use \((h, k)\) as the center and a point on the circle. Formula: \((x-h)^2 + (y-k)^2 = r^2\) where \((h, k)\) is the center and \(r\) is the radius.
Recall that a circle is the set of all points in a plane that are the same distance from the center. This definition can be used to find an equation of a circle in the coordinate plane.
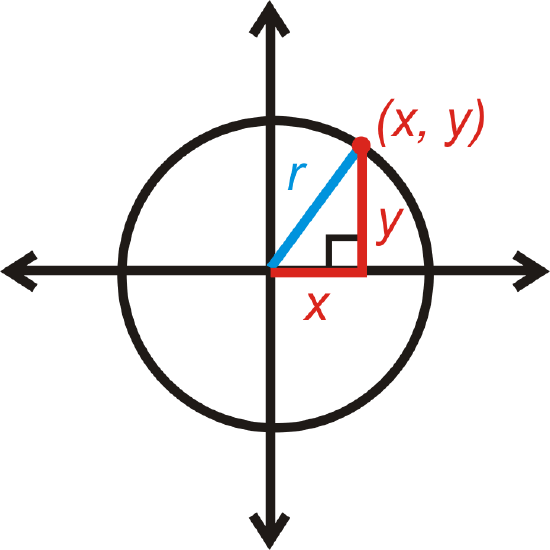
Let’s start with the circle centered at \((0, 0)\). If \((x,y)\) is a point on the circle, then the distance from the center to this point would be the radius, r. x is the horizontal distance and y is the vertical distance. This forms a right triangle. From the Pythagorean Theorem, the equation of a circle centered at the origin is \(x^2+y^2=r^2\).
The center does not always have to be on \((0, 0)\). If it is not, then we label the center \((h,k)\). We would then use the Distance Formula to find the length of the radius.
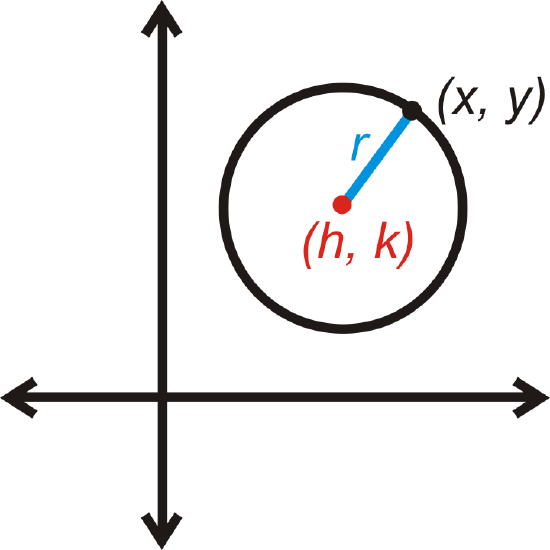
\(r=\sqrt{(x−h)^2+(y−k)^2}\)
If you square both sides of this equation, then you would have the standard equation of a circle. The standard equation of a circle with center \((h,k)\) and radius \(r\) is \(r^2=(x−h)^2+(y−k)^2\).
What if you were given the length of the radius of a circle and the coordinates of its center? How could you write the equation of the circle in the coordinate plane?
Example \(\PageIndex{1}\)
Find the center and radius of the following circle.
\((x+2)^2+(y−5)^2=49\)
Solution
Rewrite the equation as \((x−(−2))^2+(y−5)^2=7^2\). The center is \((-2, 5)\) and \(r=7\).
Keep in mind that, due to the minus signs in the formula, the coordinates of the center have the opposite signs of what they may initially appear to be.
Example \(\PageIndex{2}\)
Find the center and radius of the following circle.
Find the equation of the circle with center \((4, -1)\) and which passes through \((-1, 2)\).
Solution
First plug in the center to the standard equation.
\(\begin{aligned} (x−4)^2+(y−(−1))^2&=r^2 \\ (x−4)^2+(y+1)^2&=r^2\end{aligned}\)
Now, plug in (-1, 2) for \(x\) and \(y\) and solve for \(r\).
\(\begin{aligned} (−1−4)^2+(2+1)^2=r^2 \\ (−5)^2+(3)^2&=r^2 \\ 25+9&=r^2 \\ 34&=r^2\end{aligned}\)
Substituting in \(34\) for \(r^2\), the equation is \((x−4)^2+(y+1)^2=34\).
Example \(\PageIndex{3}\)
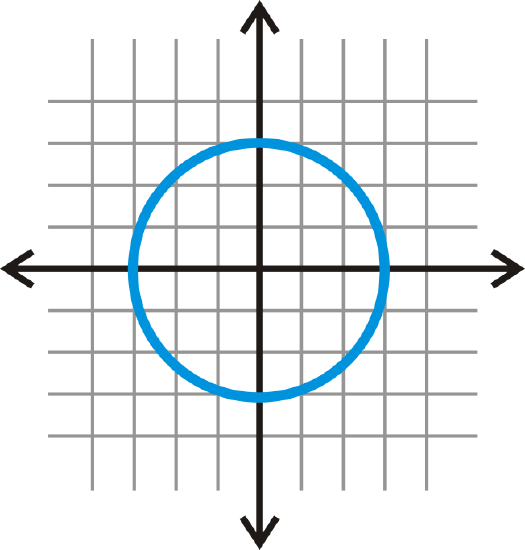
Graph \(x^2+y^2=9\).
Solution
The center is \((0, 0)\). Its radius is the square root of 9, or 3. Plot the center, plot the points that are 3 units to the right, left, up, and down from the center and then connect these four points to form a circle.
Example \(\PageIndex{4\)
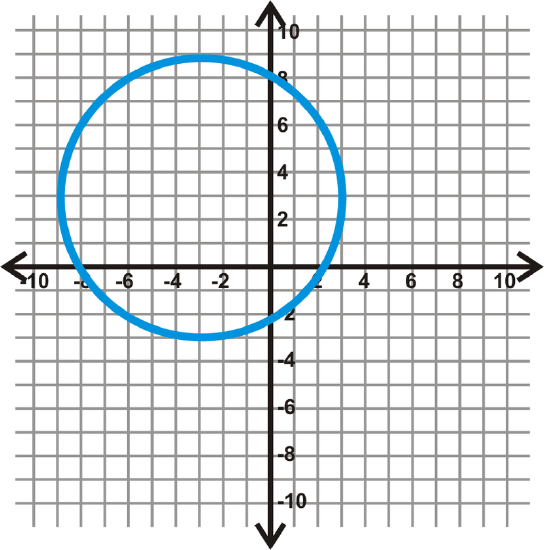
Find the equation of the circle below.
Solution
First locate the center. Draw in the horizontal and vertical diameters to see where they intersect.
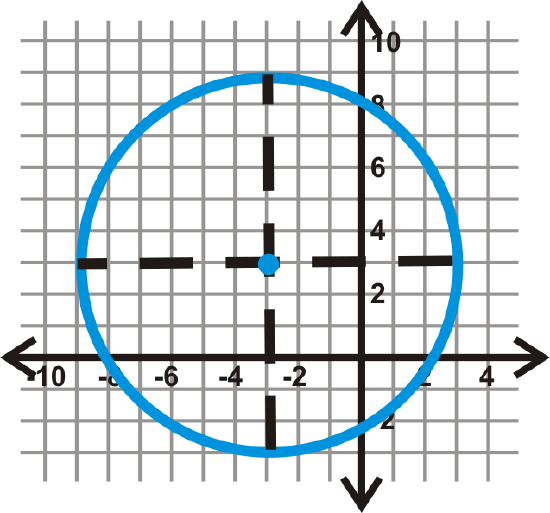
From this, we see that the center is \((-3, 3)\). If we count the units from the center to the circle on either of these diameters, we find \(r=6\). Plugging this into the equation of a circle, we get: \((x−(−3))^2+(y−3)^2=6^2\) or \((x+3)^2+(y−3)^2=36\).
Example \(\PageIndex{5}\)
Determine if the following points are on \((x+1)^2+(y−5)^2=50\).
Solution
Plug in the points for x and y in \((x+1)^2+(y−5)^2=50\).
- \((8, -3)\)
\(\begin{aligned} (8+1)^2+(−3−5)^2&=50 \\ 9^2+(−8)^2&=50 \\ 81+64 &\neq 50\end{aligned}\)
\((8, -3)\) is not on the circle
- \((-2, -2)\)
\(\begin{aligned} (−2+1)^2+(−2−5)^2&=50 \\ (−1)^2+(−7)^2&=50 \\ 1+49&=50\end{aligned}\)
\( (-2, -2)\) is on the circle
Review
Find the center and radius of each circle. Then, graph each circle.
- \((x+5)^2+(y−3)^2=16\)
- \(x^2+(y+8)^2=4
- \((x−7)^2+(y−10)^2=20
- \((x+2)^2+y^2=8
Find the equation of the circles below.
-
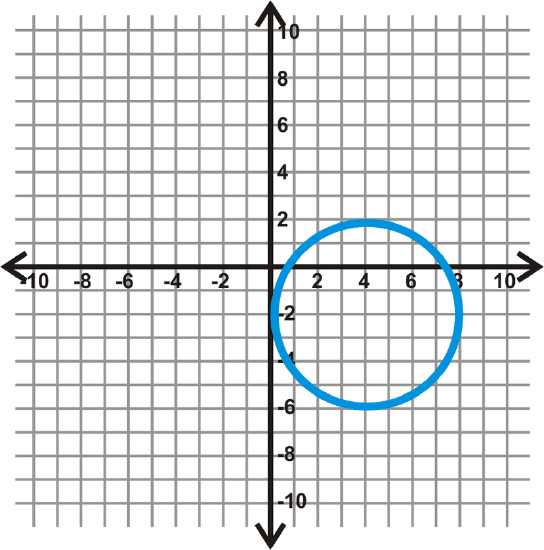
Figure \(\PageIndex{6}\) -
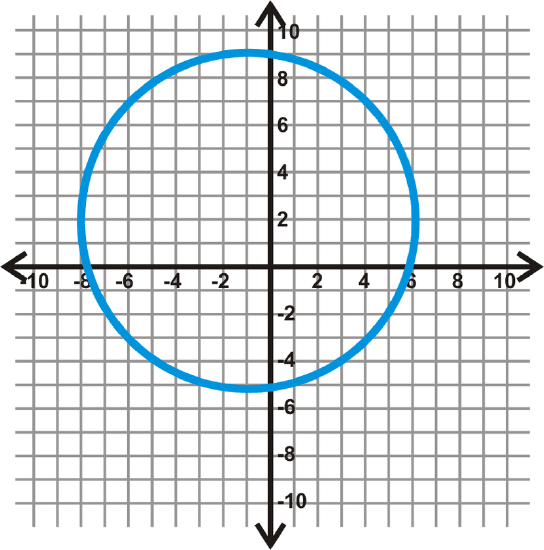
Figure \(\PageIndex{7}\) -
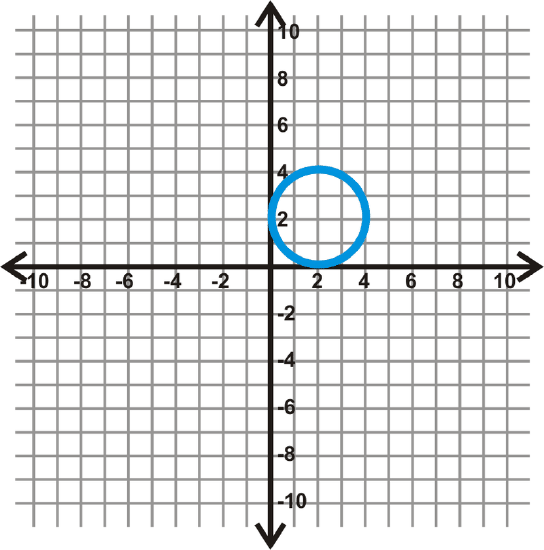
Figure \(\PageIndex{8}\) -
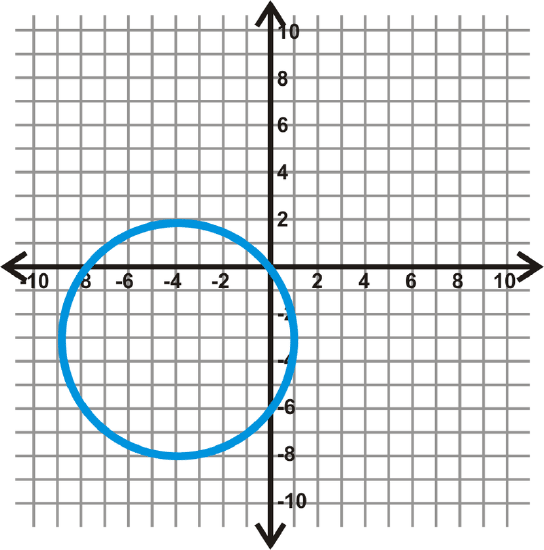
Figure \(\PageIndex{9}\) - Is (-7, 3) on \((x+1)^2+(y−6)^2=45\)?
- Is (9, -1) on \((x−2)^2+(y−2)^2=60\)?
- Is (-4, -3) on \((x+3)^2+(y−3)^2=37\)?
- Is (5, -3) on \((x+1)^2+(y−6)^2=45\)?
Find the equation of the circle with the given center and point on the circle.
- center: (2, 3), point: (-4, -1)
- center: (10, 0), point: (5, 2)
- center: (-3, 8), point: (7, -2)
- center: (6, -6), point: (-9, 4)
Review (Answers)
To see the Review answers, open this PDF file and look for section 9.12.
Vocabulary
| Term | Definition |
|---|---|
| circle | The set of all points that are the same distance away from a specific point, called the center. |
| radius | The distance from the center to the outer rim of a circle. |
| Distance Formula | The distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) can be defined as \(d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}\). |
| Origin | The origin is the point of intersection of the x and y axes on the Cartesian plane. The coordinates of the origin are (0, 0). |
Additional Resources
Interactive Element
Video: Graphing Circles Principles - Basic
Activities: Circles in the Coordinate Plane Discussion Questions
Study Aids: Properties of a Circle Study Guide
Practice: Circles in the Coordinate Plane
Real World: GPS Geometry

