2.1.7: SEC CSC COT
- Page ID
- 14183
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Secant, cosecant, cotangent values of common angles
While working to paint your grandfather's staircase, you are looking at the triangular shape made by the wall that support the stairs. The staircase looks like this:

You are thinking about all of the possible relationships between sides. You already know that there are three common relationships, called sine, cosine, and tangent.
How many others can you find?
secant, cosecant and cotangent Functions
We can define three more functions also based on a right triangle. They are the reciprocals of sine, cosine and tangent.
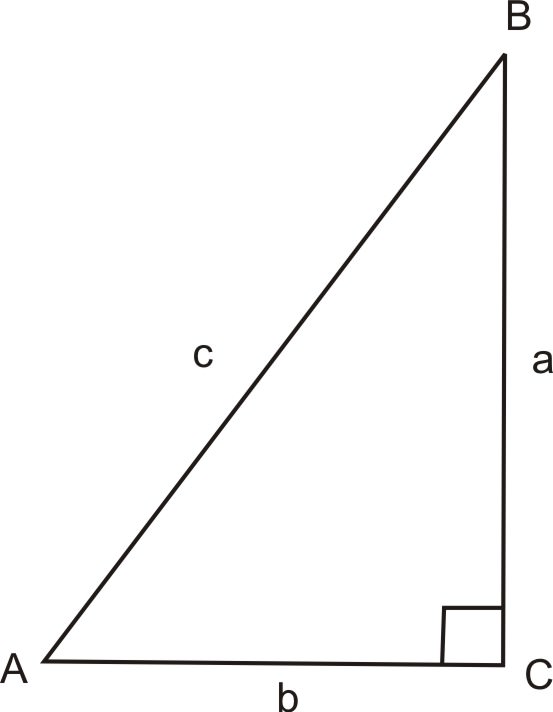
If \(\sin A=\dfrac{a}{c}\), then the definition of cosecant, or csc, is \(\csc A=\dfrac{c}{a}\).
If \(\cos A=\dfrac{b}{c}\), then the definition of secant, or sec, is \(\sec A=\dfrac{c}{b}\).
If \(\tan A=\dfrac{a}{b}\), then the definition of cotangent, or cot, is \(\cot A=\dfrac{b}{a}\).
Use the definition of secant, cosecant and cotangent to solve the following problems.
1. Find the secant, cosecant, and cotangent of angle \(B\).
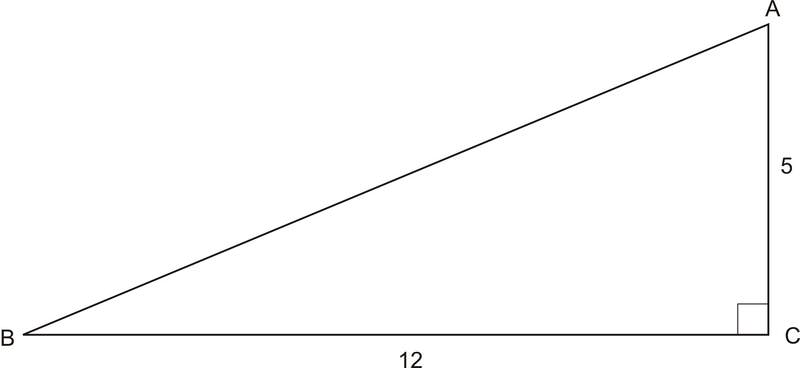
First, we must find the length of the hypotenuse. We can do this using the Pythagorean Theorem:
\(\begin{aligned}
5^{2}+12^{2} &=H^{2} \\
25+144 &=H^{2} \\
169 &=H^{2} \\
H &=13
\end{aligned}\)
Now we can find the secant, cosecant, and cotangent of angle B:
\(\begin{array}{l}
\sec B=\dfrac{\text { hypotenuse }}{\text { adjacent side }}=\dfrac{13}{12} \\
\csc B=\dfrac{\text { hypotenuse }}{\text { opposite side }}=\dfrac{13}{5} \\
\cot B=\dfrac{\text { adjacent side }}{\text { opposite side }}=\dfrac{12}{5}
\end{array}\)
2. Find the secant, cosecant, and cotangent of angle A
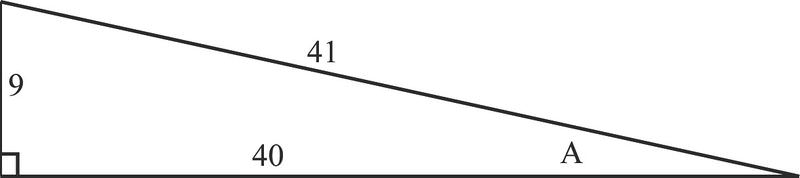
\(\begin{array}{l}
\sec A=\dfrac{\text { hypotenuse }}{\text { adjacent side }}=\dfrac{41}{40} \\
\csc A=\dfrac{\text { hypotenuse }}{\text { opposite side }}=\dfrac{41}{9} \\
\cot A=\dfrac{\text { adjacent side }}{\text { opposite side }}=\dfrac{40}{9}
\end{array}\)
3. Find the sine, cosine, and tangent of angle \(A\), and then use this to construct the secant, cosecant, and cotangent of the angle
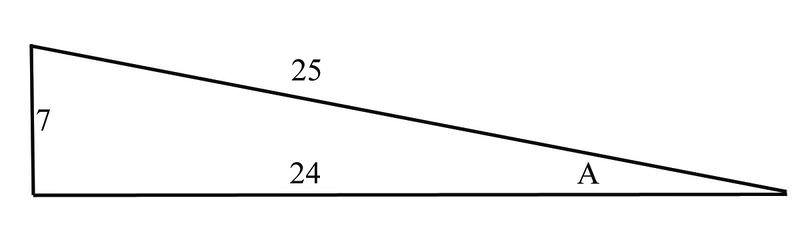
\(\begin{array}{l}
\sin A=\dfrac{\text { opposite side }}{\text { hypotenuse }}=\dfrac{7}{25} \\
\cos A=\dfrac{\text { adjacent side }}{\text { hypotenuse }}=\dfrac{24}{25} \\
\tan A=\dfrac{\text { opposite side }}{\text { adjacent side }}=\dfrac{7}{24}
\end{array}\)
Since we know that cosecant is the reciprocal of sine, secant is the reciprocal of sine, and cotangent is the reciprocal of tangent, we can construct these functions as follows:
\(\begin{array}{l}
\sec A=\dfrac{1}{\cos A}=\dfrac{25}{24} \\
\csc A=\dfrac{1}{\sin A}=\dfrac{25}{7} \\
\cot A=\dfrac{1}{\tan A}=\dfrac{24}{7}
\end{array}\)
Earlier, you were given a problem about your grandfather's staircase.
Looking at a triangle-like the shape of the wall supporting your grandfather's staircase:

Solution
We can see that there are several ways to make relationships between the sides. In this case, we are only interested in ratios between the sides, which means one side will be divided by another. We've already seen some functions, such as:
1) The side opposite the angle divided by the hypotenuse (the sine function)
2) The side adjacent the angle divided by the hypotenuse (the cosine function)
3) The side opposite the angle divided by adjacent side (the tangent function)
In this section we introduced the reciprocal of the above trig functions. These are found by taking ratios between the same sides shown above, except reversing the numerator and denominator:
4) The hypotenuse divided by the side opposite the angle (the cosecant function)
5) The hypotenuse divided by the side adjacent to the angle (the secant function)
6) The adjacent side divided by the opposite side (the cotangent function)
Use the figure below to help solve the following examples.
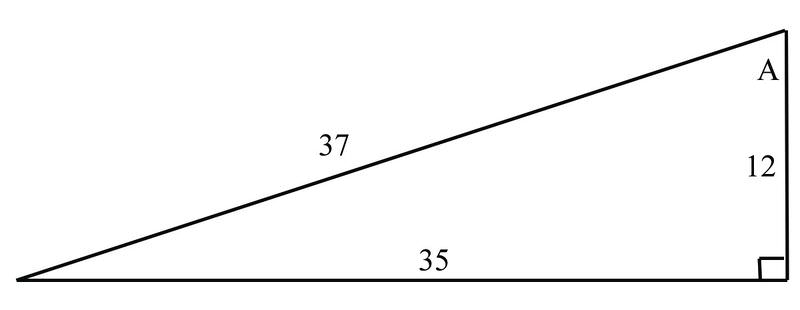
Find the secant \(\angle A\)
Solution
The secant function is defined to be \(\dfrac{1}{\cos}\). Since \(\cos=\dfrac{\text{adjacent}}{\text{hypotenuse}}\), \(\sec=\dfrac{\text{hypotenuse}}{\text{adjacent}}\).
\(\sec=\dfrac{\text{hypotenuse}}{\text{adjacent}}=\dfrac{37}{12}\approx 3.08\)
Find the cosecant of \(\angle A\)
Solution
The cosecant function is defined to be \(\dfrac{1}{\sin}\). Since \(\sin=\dfrac{\text{opposite}}{\text{hypotenuse}}\), \(\csc=\dfrac{\text{hypotenuse}}{\text{opposite}}\).
\(\csc=\dfrac{\text{hypotenuse}}{\text{opposite}}=\dfrac{37}{35}\approx 1.06\)
Find the cotangent of \(\angle A\)
Solution
The cotangent function is defined to be \(\dfrac{1}{\tan}\). Since \(\tan=\dfrac{\text{opposite}}{\text{adjacent}}\), \(\cot=\dfrac{\text{adjacent}}{\text{opposite}}\).
\(\cot=\dfrac{\text{adjacent}}{\text{opposite}}=\dfrac{12}{35} \approx .34\)
Review
Use the diagram below for questions 1-3.
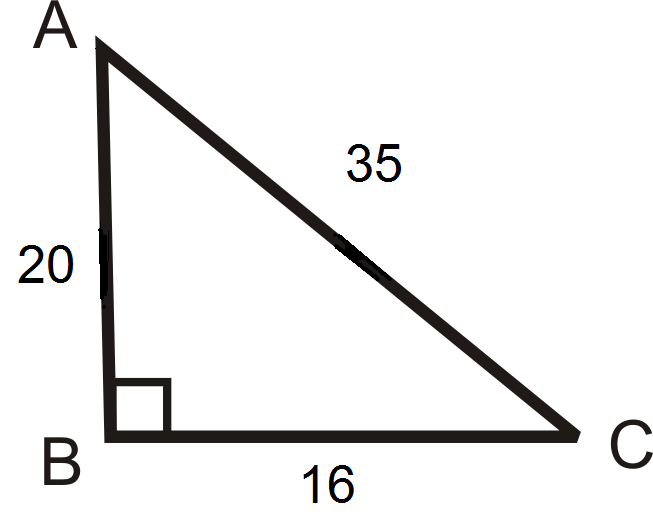
- Find \(\csc A\) and \(\csc C \).
- Find \(\sec A\) and \(\sec C\).
- Find \(\cot A\) and \(\cot C\).
Use the diagram to fill in the blanks below.
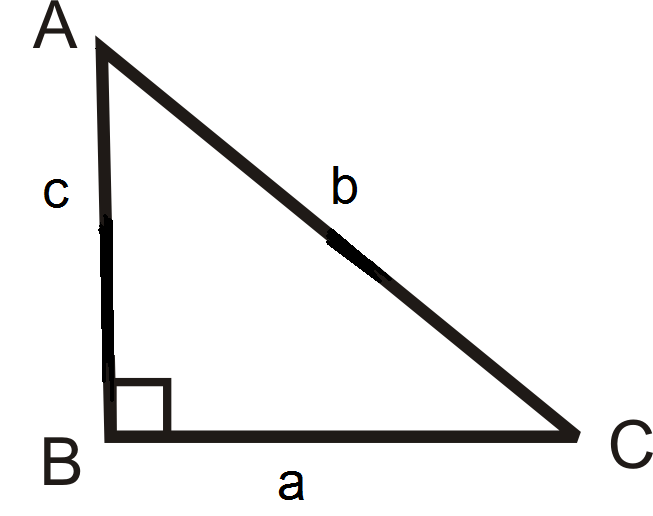
- \(\cot A=\dfrac{?}{?}\)
- \(\csc C =\dfrac{?}{?}\)
- \(\cot C=\dfrac{?}{?}\)
- \(\sec C=\dfrac{?}{?}\)
- \(\csc A=\dfrac{?}{?}\)
- \(\sec A=\dfrac{?}{?}\)
From questions 4-9, we can conclude the following. Fill in the blanks.
- \(\sec \text{_____}=\csc A\) and \(\csc \text{_____}=\sec A\).
- \(\cot A\) and \(\cot C\) are _________ of each other.
- Explain why the csc of an angle will always be greater than 1.
- Use your knowledge of 45-45-90 triangles to find the cosecant, secant, and cotangent of a 45 degree angle.
- Use your knowledge of 30-60-90 triangles to find the cosecant, secant, and cotangent of a 30 degree angle.
- Use your knowledge of 30-60-90 triangles to find the cosecant, secant, and cotangent of a 60 degree angle.
- As the degree of an angle increases, will the cotangent of the angle increase or decrease? Explain.
Review (Answers)
To see the Review answers, open this PDF file and look for section 1.9.
Vocabulary
| Term | Definition |
|---|---|
| cosecant | The cosecant of an angle in a right triangle is a relationship found by dividing the length of the hypotenuse by the length of the side opposite to the given angle. This is the reciprocal of the sine function. |
| cotangent | The cotangent of an angle in a right triangle is a relationship found by dividing the length of the side adjacent to the given angle by the length of the side opposite to the given angle. This is the reciprocal of the tangent function. |
| secant | The secant of an angle in a right triangle is the value found by dividing length of the hypotenuse by the length of the side adjacent the given angle. The secant ratio is the reciprocal of the cosine ratio. |

