2.1.1: Right Triangle Trigonometry

Last updated

Mar 27, 2022
Save as PDF
- 2.1: Trig Functions
- 2.1.2: Calculator Trig Functions

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Sine, cosine, tangent, and other ratios of sides of a right triangle.

Sine, Cosine, and Tangent

Trigonometry is the study of the relationships between the sides and angles of right triangles. The legs are called adjacent or opposite depending on which acute angle is being used.

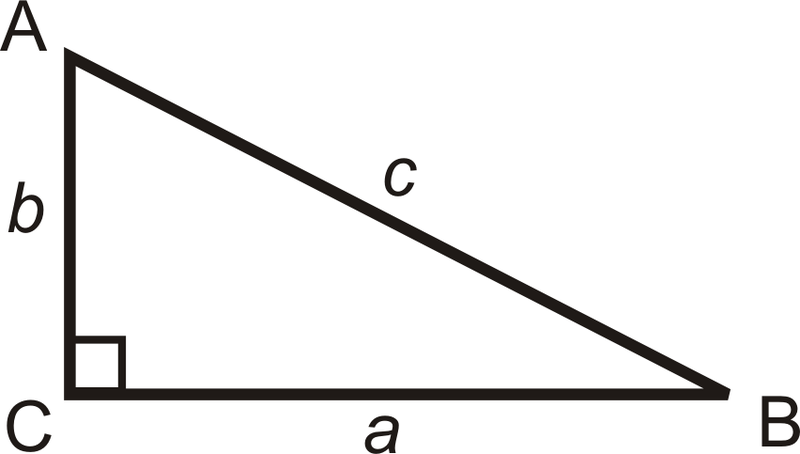
f-d_2a337f0fc303f5ead45b9c00ac0b99fc56d2875b59312a4bb58a17d7+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{1}$

$\begin{aligned} a \text{ is adjacent to } \angle B \qquad a \text{ is opposite } \angle A \\ b \text{ is adjacent to } \angle A \qquad b \text{ is opposite } \angle B\\ c \text{ is the hypotenuse }\end{aligned}$

The three basic trigonometric ratios are called sine, cosine and tangent. For right triangle △ABC, we have:

$\begin{aligned} \text { sine Ratio: } \dfrac{\text {opposite leg}}{\text {hypotenuse}} \qquad \sin A=\dfrac{a}{c} \text { or } \sin B=\dfrac{b}{c}\\ \text { cosine Ratio: } \dfrac{\text {adjacent leg}}{\text {hypotenuse}} \qquad \cos A=\dfrac{b}{c} \text { or } \cos B=\dfrac{a}{c}\\ \text { Tangent Ratio: } \dfrac{\text {opposite leg}}{\text {adjacent leg}} \qquad \tan A=\dfrac{a}{b} \text { or } \tan B=\dfrac{b}{a} \end{aligned}$

An easy way to remember ratios is to use SOH-CAH-TOA.

f-d_f1f7a87f733a90695f2ea8c27f27adfe99b8c302701f230c8a651303+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{2}$

A few important points:

Always reduce ratios (fractions) when you can.
Use the Pythagorean Theorem to find the missing side (if there is one).
If there is a radical in the denominator, rationalize the denominator.

What if you were given a right triangle and told that its sides measure 3, 4, and 5 inches? How could you find the sine, cosine, and tangent of one of the triangle's non-right angles?

Example $\PageIndex{1}$

Find the sine, cosine and tangent ratios of $\angle A$ .

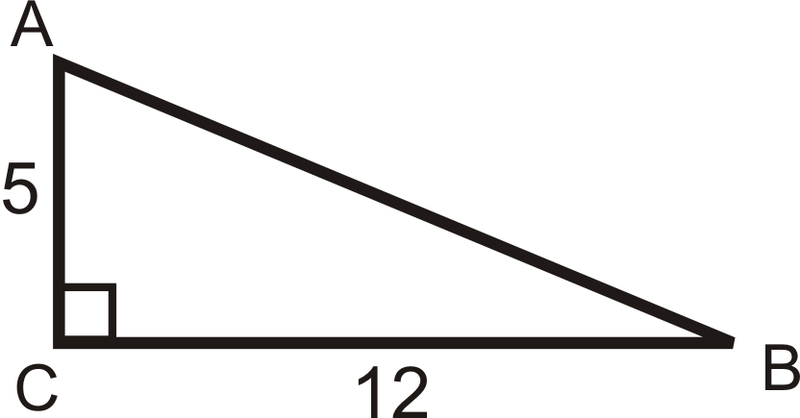
f-d_031ebbc297b0cdd97c0feecc07fe317f71669d1ad5c7ba3d542eee27+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{3}$

Solution

First, we need to use the Pythagorean Theorem to find the length of the hypotenuse.

$\begin{aligned} 5^{2}+12^{2} &=c^{2} \\ 13 &=c \end{aligned}$

$\begin{aligned} \sin A &=\dfrac{l e g \text { opposite } \angle A}{\text {hypotenuse}}=\dfrac{12}{13} & \cos A=\dfrac{\text {leg adjacent to } \angle A}{\text {hypotenuse}}=\dfrac{5}{13}, \\ \tan A &=\dfrac{\text {leg opposite } \angle A}{\text {leg adjacent to } \angle A}=\dfrac{12}{5} \end{aligned}$

Example $\PageIndex{2}$

Find the sine, cosine, and tangent of $\angle B$ .

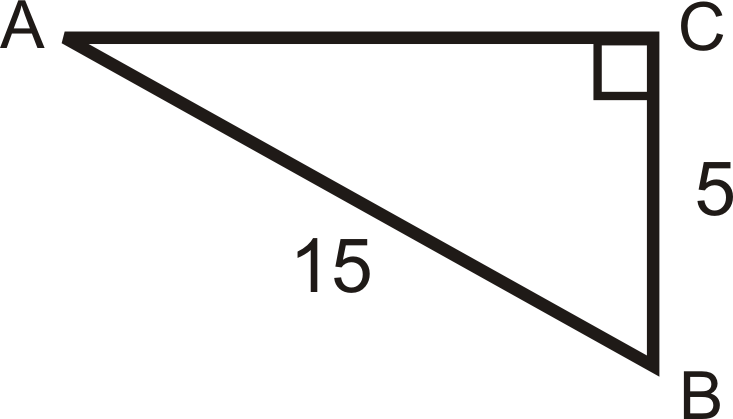
f-d_b3ba5ef84e1a917e66872b19f11be0f149e6bb87a55928778692eab4+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{4}$

Find the length of the missing side.

Solution

$\begin{aligned} A C^{2}+5^{2} &=15^{2} \\ A C^{2} &=200 \\ A C &=10 \sqrt{2} \end{aligned}$

$\begin{aligned}\sin B &=\dfrac{10 \sqrt{2}}{15}=\dfrac{2 \sqrt{2}}{3} \quad \cos B=\dfrac{5}{15}=\dfrac{1}{3} \quad \tan B=\dfrac{10 \sqrt{2}}{5}=2 \sqrt{2} \end{aligned}$

Example $\PageIndex{3}$

Find the sine, cosine and tangent of $30^{\circ}$ .

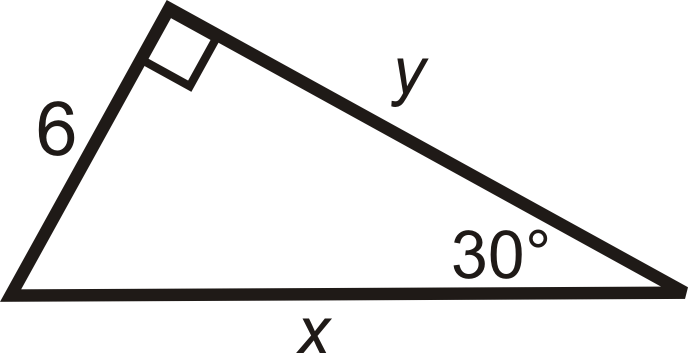
f-d_d737dd8b54519801f1f37eb3ee5bfeab056fcf56a560b006b021f64e+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{5}$

Solution

This is a 30-60-90 triangle. The short leg is 6, $y=6\sqrt{3}$ and $x=12$ .

$\sin 30^{\circ}=\dfrac{6}{12}=\dfrac{1}{2} \qquad \cos30^{\circ}=\dfrac{6\sqrt{3}}{12}=\dfrac{\sqrt{3}}{2} \qquad \tan 30^{\circ}=\dfrac{6}{6\sqrt{3}}=\dfrac{1}{\sqrt{3}}\cdot \dfrac{\sqrt{3}}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}$

Example $\PageIndex{4}$

Answer the questions about the following image. Reduce all fractions.

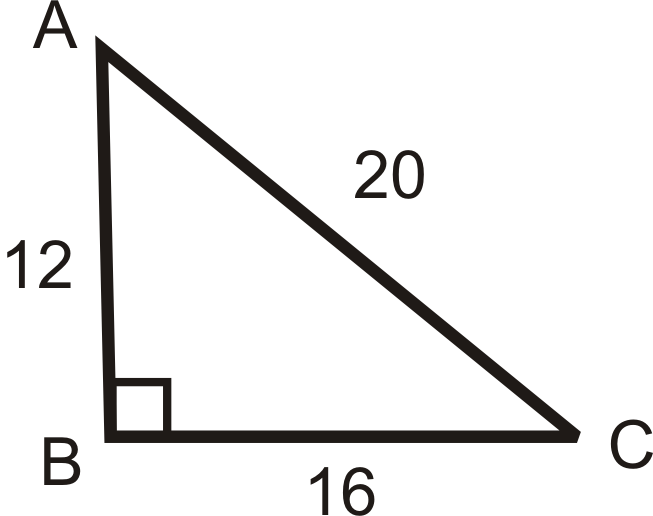
f-d_82dc3857b48da6c9ea0c59b6c0cc430bc0c50507f0e3043ba59ce98a+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{6}$

What is $\sin A$ , $\cos A$ , and $\tan A$ ?

Solution

$\begin{array}{l} \sin A=\dfrac{16}{20}=\dfrac{4}{5} \\ \cos A=\dfrac{12}{20}=\dfrac{3}{5} \\ \tan A=\dfrac{16}{12}=\dfrac{4}{3} \end{array}$

Review

Use the diagram to fill in the blanks below.

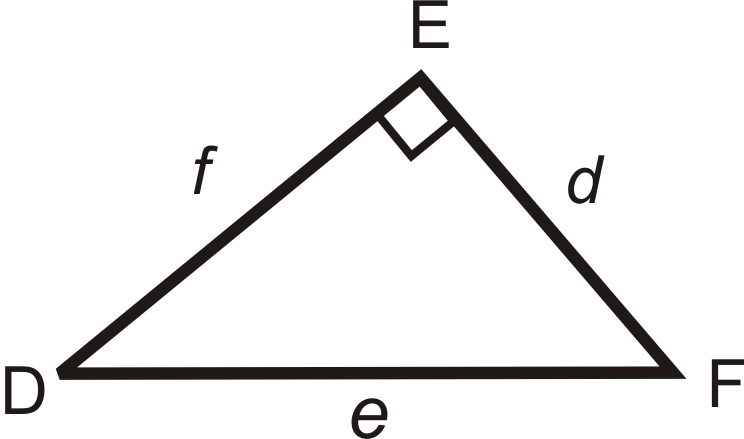
f-d_18318d6aa8951562a8c2282678934fc7f4ab7335f4714faf5ef3a831+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{7}$

$\tan D=\dfrac{?}{?}$
$\sin F=\dfrac{?}{?}$
$\tan F=\dfrac{?}{?}$
$\cos F=\dfrac{?}{?}$
$\sin D=\dfrac{?}{?}$
$\cos D=\dfrac{?}{?}$

From questions 1-6, we can conclude the following. Fill in the blanks.

$\cos \underline{\qquad}=\sin F$ and $\sin \underline{\qquad}=\cos F$ .
$\tan D$ and $\tan F$ are _________ of each other.

Find the sine, cosine and tangent of $\angle A$ . Reduce all fractions and radicals.

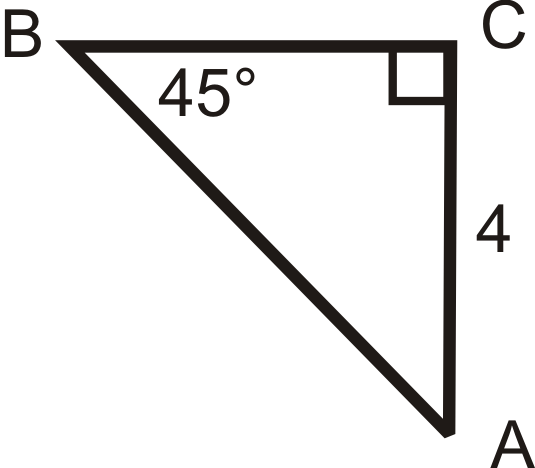
Figure $\PageIndex{8}$
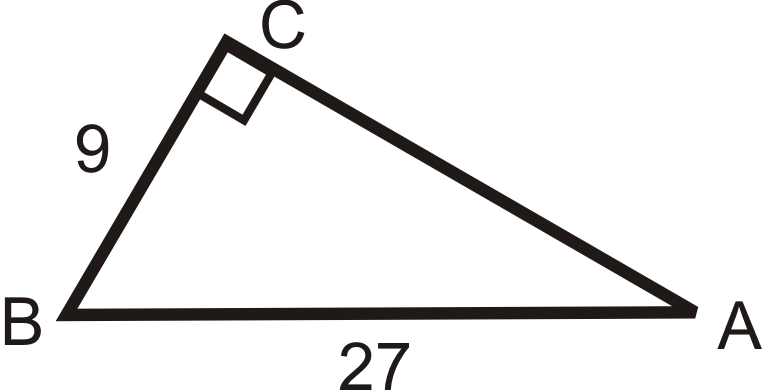
Figure $\PageIndex{9}$
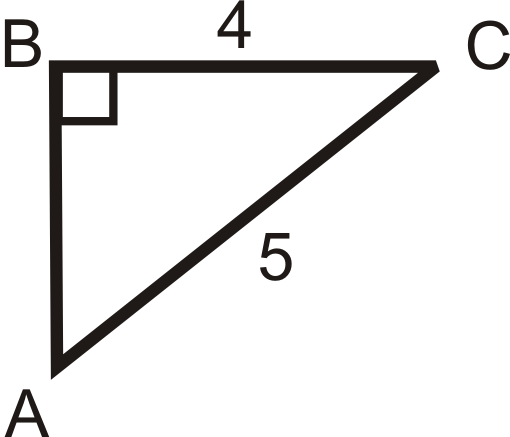
Figure $\PageIndex{10}$
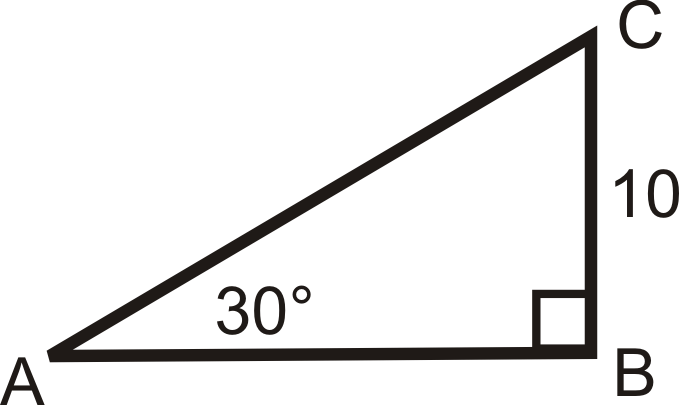
Figure $\PageIndex{11}$
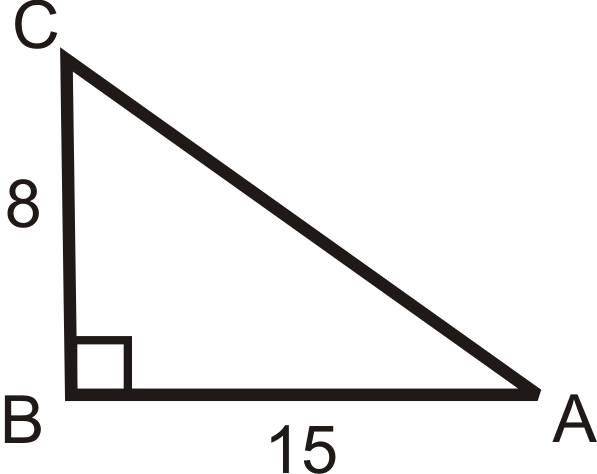Figure $\PageIndex{12}$

Review (Answers)

To see the Review answers, open this PDF file and look for section 8.7.

Resources

Vocabulary

Term	Definition
Acute Angle	An acute angle is an angle with a measure of less than 90 degrees.
Adjacent Angles	Two angles are adjacent if they share a side and vertex. The word 'adjacent' means 'beside' or 'next-to'.
Hypotenuse	The hypotenuse of a right triangle is the longest side of the right triangle. It is across from the right angle.
Legs of a Right Triangle	The legs of a right triangle are the two shorter sides of the right triangle. Legs are adjacent to the right angle.
opposite	The opposite of a number $x$ is $−x$ . A number and its opposite always sum to zero.
Pythagorean Theorem	The Pythagorean Theorem is a mathematical relationship between the sides of a right triangle, given by $a^2+b^2=c^2$ , where a and b are legs of the triangle and c is the hypotenuse of the triangle.
Radical	The $\sqrt$ , or square root, sign.
sine	The sine of an angle in a right triangle is a value found by dividing the length of the side opposite the given angle by the length of the hypotenuse.
Trigonometric Ratios	Ratios that help us to unders\tan d the relationships between sides and angles of right triangles.

Additional Resources

Interactive Element

Video: Introduction to Trigonometric Functions U\sin g Triangles

Activities: Sine, cosine, Tangent Discussion Questions

Study Aids: Trigonometric Ratios Study Guide

Practice: Right Triangle Trigonometry

Real World: Sine cosine Tangent