2.7: Deductive Reasoning
- Page ID
- 2147
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Drawing conclusions from facts.
Deductive reasoning entails drawing conclusion from facts. When using deductive reasoning there are a few laws that are helpful to know.
Law of Detachment: If \(p\rightarrow q\) is true, and \(p\) is true, then \(q\) is true. See the example below.
Here are two true statements:
- If a number is odd (p), then it is the sum of an even and odd number (q).
- 5 is an odd number (a specific example of p).
The conclusion must be that 5 is the sum of an even and an odd number (q).
Law of Contrapositive: If \(p\rightarrow q\) is true and \(\sim q\) is true, then you can conclude \(\sim p\). See the example below.
Here are two true statements:
- If a student is in Geometry (\(p\)), then he or she has passed Algebra I (\(q\)).
- Daniel has not passed Algebra I (a specific example of \(\sim q\)).
The conclusion must be that Daniel is not in Geometry (\(\sim q\)).
Law of Syllogism: If \(p\rightarrow q\) and \(q\rightarrow r\) are true, then \(p\rightarrow r\) is true. See the example below.
Here are three true statements:
- If Pete is late (\(p\)), Mark will be late (\(q\)).
- If Mark is late (\(q\)), Karl will be late (\(r\)).
- Pete is late (\(p\)).
Notice how each “then” becomes the next “if” in a chain of statements. If Pete is late, this starts a domino effect of lateness. Mark will be late and Karl will be late too. So, if Pete is late, then Karl will be late (\(r\)), is the logical conclusion.
What if you were given a fact like "If you are late for class, you will get a detention"? What conclusions could you draw from this fact?
Example \(\PageIndex{1}\)
Suppose Bea makes the following statements, which are known to be true.
If Central High School wins today, they will go to the regional tournament. Central High School won today.
What is the logical conclusion?
Solution
These are true statements that we can take as facts. The conclusion is: Central High School will go to the regional tournament.
Example \(\PageIndex{2}\)
Here are two true statements.
If \(\angle A\) and \(\angle B\) are a linear pair, then \(m\angle A+m\angle B=180^{\circ}\).
\(\angle ABC\) and \(\angle CBD\) are a linear pair.
What conclusion can you draw from this?
Solution
This is an example of the Law of Detachment, therefore:
\(m\angle ABC+m\angle CBD=180^{\circ}\)
Example \(\PageIndex{3}\)
Determine the conclusion from the true statements below.
Babies wear diapers.
My little brother does not wear diapers.
Solution
The second statement is the equivalent of \(\sim q\). Therefore, the conclusion is \(\sim p\), or: My little brother is not a baby.
Example \(\PageIndex{4}\)
Here are two true statements.
If \(\angle A\) and \(\angle B\) are a linear pair, then \(m\angle A+m\angle B=180^{\circ}\).
\(m\angle 1=90^{\circ}\) and \(m\angle 2=90^{\circ}\).
What conclusion can you draw from these two statements?
Solution
Here there is NO conclusion. These statements are in the form:
\(p \rightarrow q\)
\(q\)
We cannot conclude that \(\angle 1\) and \(\angle 2\) are a linear pair.
Here are two counterexamples:
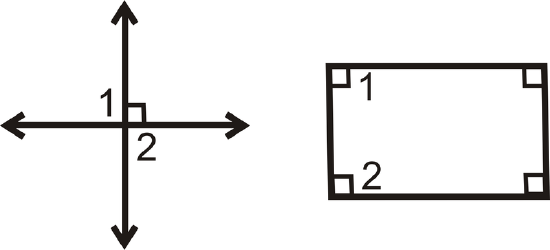Figure \(\PageIndex{1}\)Example \(\PageIndex{5}\)
Determine the conclusion from the true statements below.
If you are not in Chicago, then you can’t be on the \(L\).
Sally is on the \(L\).
Solution
If we were to rewrite this symbolically, it would look like:
\(\sim p \rightarrow \sim q\)
\(q\)
Even though it looks a little different, this is an example of the Law of Contrapositive. Therefore, the logical conclusion is: Sally is in Chicago.
Review
Determine the logical conclusion and state which law you used (Law of Detachment, Law of Contrapositive, or Law of Syllogism). If no conclusion can be drawn, write “no conclusion.”
- People who vote for Jane Wannabe are smart people. I voted for Jane Wannabe.
- If Rae is the driver today then Maria is the driver tomorrow. Ann is the driver today.
- All equiangular triangles are equilateral. \(\delta ABC\) is equiangular.
- If North wins, then West wins. If West wins, then East loses.
- If \(z>5\), then \(x>3\). If \(x>3\), then \(y>7\).
- If I am cold, then I wear a jacket. I am not wearing a jacket.
- If it is raining outside, then I need an umbrella. It is not raining outside.
- If a shape is a circle, then it never ends. If it never ends, then it never starts. If it never starts, then it doesn’t exist. If it doesn’t exist, then we don’t need to study it.
- If you text while driving, then you are unsafe. You are a safe driver.
- If you wear sunglasses, then it is sunny outside. You are wearing sunglasses.
- If you wear sunglasses, then it is sunny outside. It is cloudy.
- I will clean my room if my mom asks me to. I am not cleaning my room.
- Write the symbolic representation of #8. Include your conclusion. Does this argument make sense?
- Write the symbolic representation of #10. Include your conclusion.
- Write the symbolic representation of #11. Include your conclusion.
Resources
Vocabulary
| Term | Definition |
|---|---|
| Deductive Reasoning | When using deductive reasoning, one would draw conclusions that are based on facts. |
Additional Resources
Video: Types of Reasoning: Deductive Principles - Basic
Activities: Deductive Reasoning Discussion Questions
Study Aids: Types of Reasoning Study Guide
Practice: Deductive Reasoning
Real World: Deductive Reasoning