2.8: Truth Tables
- Page ID
- 2146
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)So far we know these symbols for logic:
- \(\sim\) not (negation)
- \(\rightarrow\) if-then
- \(\therefore\) therefore
Two more symbols are:
- \(\wedge\) and
- \(\lor\) or
We would write “\(p\) and \(q\)” as \(p\wedge q\) and “\(p\) or \(q\)” as \(p\lor q\).
Truth tables use these symbols and are another way to analyze logic. First, let’s relate p and \sim p. To make it easier, set p as: An even number. Therefore, \sim p is An odd number. Make a truth table to find out if they are both true. Begin with all the “truths” of p, true (T) or false (F).
| p | |
|---|---|
| T | |
| F |
Next we write the corresponding truth values for \(\sim p\). \(\sim p\) has the opposite truth values of \(p\). So, if \(p\) is true, then \(\sim p\) is false and vise versa.
| p | \sim p |
|---|---|
| T | F |
| F | T |
To Recap:
- Start truth tables with all the possible combinations of truths. For 2 variables there are 4 combinations for 3 variables there are 8. You always start a truth table this way.
- Do any negations on the any of the variables.
- Do any combinations in parenthesis.
- Finish with completing what the problem was asking for.
Drawing a Truth Table
1. Draw a truth table for \(p\), \(q\) and \(p \wedge q\).
First, make columns for p and q. Fill the columns with all the possible true and false combinations for the two.
| p | q | |
|---|---|---|
| T | T | |
| T | F | |
| F | T | |
| F | F |
Notice all the combinations of p and q. Anytime we have truth tables with two variables, this is always how we fill out the first two columns.
Next, we need to figure out when \(p\wedge q\) is true, based upon the first two columns. p \wedge q can only be true if BOTH p and q are true. So, the completed table looks like this:
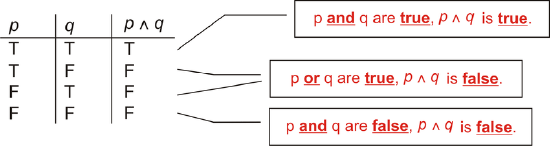Figure \(\PageIndex{1}\)This is how a truth table with two variables and their “and” column is always filled out.
2. Draw a truth table for \(p\), \(q\) and \(p \lor q\).
First, make columns for \(p \lor q\) and \(q\), just like Example A.
| p | q | |
|---|---|---|
| T | T | |
| T | F | |
| F | T | |
| F | F |
Next, we need to figure out when \(p \lor q\) is true, based upon the first two columns. \(p \lor q\) is true if \(p\) OR \(q\) are true, or both are true. So, the completed table looks like this:
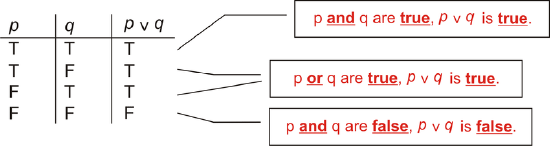Figure \(\PageIndex{2}\)The difference between \(p \wedge q\) and \(p \lor q\) is the second and third rows. For “and” both \(p\) and \(q\) have to be true, but for “or” only one has to be true.
Determining the Truths of Variables
Determine the truths for \(p \wedge(\sim q \lor r)\).
First, there are three variables, so we are going to need all the combinations of their truths. For three variables, there are always 8 possible combinations.
| \(p\) | \(q\) | \(r\) | |||
|---|---|---|---|---|---|
| T | T | T | |||
| T | T | F | |||
| T | F | T | |||
| T | F | F | |||
| F | T | T | |||
| F | T | F | |||
| F | F | T | |||
| F | F | F |
Next, address the \(\sim q\). It will just be the opposites of the \(q\) column.
| \(p\) | \(q\) | \(r\) | \(\sim q\) | ||
|---|---|---|---|---|---|
| T | T | T | F | ||
| T | T | F | F | ||
| T | F | T | T | ||
| T | F | F | T | ||
| F | T | T | F | ||
| F | T | F | F | ||
| F | F | T | T | ||
| F | F | F | T |
Now, let’s do what’s in the parenthesis, \(\sim q\lor r\). Remember, for “or” only \(\sim q\) OR \(r\) has to be true. Only use the \(\sim q\) and \(r\) columns to determine the values in this column.
| \(p\) | \(q\) | \(r\) | \(\sim q\) | \(\sim q\lor r\) | |
|---|---|---|---|---|---|
| T | T | T | F | T | |
| T | T | F | F | F | |
| T | F | T | T | T | |
| T | F | F | T | T | |
| F | T | T | F | T | |
| F | T | F | F | F | |
| F | F | T | T | T | |
| F | F | F | T | T |
Finally, we can address the entire problem, \(p \wedge(\sim q \lor r)\). Use the \(p\) and \(\sim q\lor r\) to determine the values. Remember, for “and” both \(p\) and \(\sim q\lor r\) must be true.
| \(p\) | \(q\) | \(r\) | \(\sim q\) | \(\sim q\lor r\) | \(p \wedge(\sim q \lor r)\) |
|---|---|---|---|---|---|
| T | T | T | F | T | T |
| T | T | F | F | F | F |
| T | F | T | T | T | T |
| T | F | F | T | T | T |
| F | T | T | F | T | F |
| F | T | F | F | F | F |
| F | F | T | T | T | F |
| F | F | F | T | T | F |
Write a truth table for the following variables.
Example \(\PageIndex{1}\)
\(p \wedge \sim p\)
Solution
First, make columns for \(p\), then add in \(\sim p\) and finally, evaluate \(p \wedge \sim p\).
| \(p\) | \(\sim p\) | \(p \wedge \sim p\) |
|---|---|---|
| T | F | F |
| F | T | F |
Example \(\PageIndex{2}\)
\(\sim p \lor \sim q\)
Solution
First, make columns for \(p\) and \(q\), then add in \(\sim p\) and \(\sim q\). Finally, evaluate \(\sim p \lor \sim q\).
| \(p\) | \(q\) | \(\sim p\) | \(\sim q\) | \(\sim p \lor \sim q\) |
|---|---|---|---|---|
| \(p \lor \sim q\) | T | F | F | F |
| T | F | F | T | T |
| F | T | T | F | T |
| F | F | T | T | T |
Example \(\PageIndex{3}\)
\(p \wedge (q\lor \sim q)\)
Solution
First, make columns for p and q, then add in \(\sim q\) and \(q\lor \sim q\). Finally, evaluate \(p\wedge (q\lor \sim q)\).
| \(p\) | \(q\) | \(\sim q\) | \(q\lor \sim q\) | \(p\wedge (q\lor \sim q)\) |
|---|---|---|---|---|
| T | T | F | T | T |
| T | F | T | T | T |
| F | T | F | T | F |
| F | F | T | T | F |
Review
Write a truth table for the following variables.
- \((p \wedge q)\lor \sim r\)
- \(p \lor ( \sim q \lor r)\)
- \(p \wedge (q \lor \sim r)\)
- The only difference between #1 and #3 is the placement of the parenthesis. How do the truth tables differ?
- When is \(p \lor q \lor r\) true?
- \(p \lor q \lor r\)
- \((p \lor q) \lor \sim r\)
- \(( \sim p \wedge \sim q) \wedge r\)
- \(( \sim p \lor \sim q) \wedge r\)
Is the following a valid argument? If so, what law is being used? HINT: Statements could be out of order.
\(p \rightarrow q\)
\(r \rightarrow p\)
\(\therefore r \rightarrow q\)
\(p \rightarrow q\)
\(r \rightarrow q\)
\(\therefore p \rightarrow r\)
\(p \rightarrow \sim r\)
\(r \)
\(\therefore \sim p\)
\(\sim q \rightarrow r\)
\(q \)
\(\therefore \sim r\)
\(p \rightarrow (r \rightarrow s)\)
\(p \)
\(\therefore r \rightarrow s\)
\(r \rightarrow q\)
\(r \rightarrow s \)
\(\therefore q \rightarrow s\)
Additional Resources
Video: Truth Tables Principles
Practice: Truth Tables