2.15: Proofs- Angle Pairs and Segments
- Page ID
- 7187
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Vertical angles, perpendicular bisectors, and other theorems based on intersecting lines or parallel lines and a transversal.
Theorems about Lines and Angles
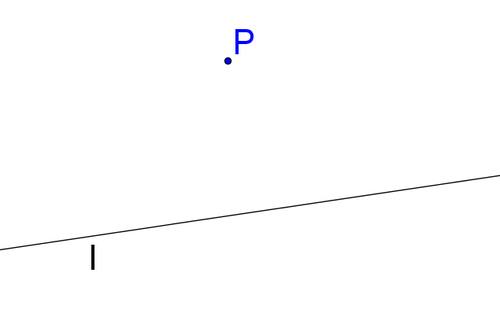
Consider line \(l\) and a point \(P\) that is not on line \(l\). How many lines exist that are parallel to \(l\) and pass through point \(P\)?
Line and Angle Theorems
Consider two parallel lines that are intersected by a third line. (Remember that tick marks (≫) can be used to indicate that two lines are parallel.)
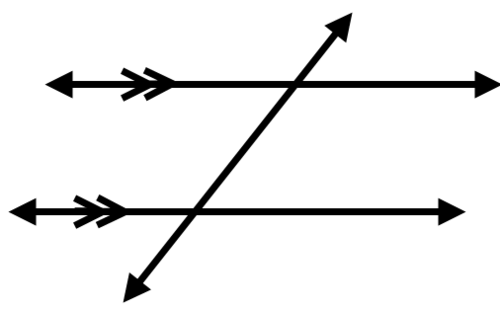
This third line is called a transversal. Note that four angles are created where the transversal intersects each line. Each angle created by the transversal and the top line has a corresponding angle with an angle create by the transversal and the bottom line. These corresponding angle pairs are shown color-coded below. How do you think these corresponding angles are related?

Your intuition and knowledge of translations might suggest that these angles are congruent. Imagine translating one of the angles along the transversal until it meets the second parallel line. It will match its corresponding angle exactly. This is known as the corresponding angle postulate:
If two parallel lines are cut by a transversal, then the corresponding angles are congruent.
Remember that a postulate is a statement that is accepted as true without proof. Your knowledge of translations should convince you that this postulate is true.
Resources
Let's take a look at some example problems.
1. Recall that vertical angles are a pair of opposite angles created by intersecting lines. Prove that vertical angles are congruent.
For this proof, you are not given a specific picture. When not given a picture, it helps to create a generic picture to reference in your proof. It's important that the picture does not include any information that you cannot assume. Below is a generic picture of intersecting lines with angles numbered for reference.
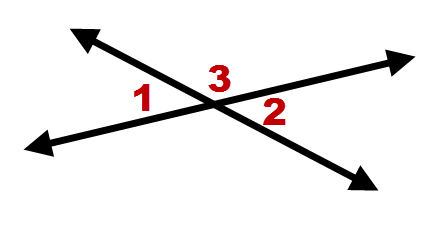
In this picture, \(\angle 1\) and \(\angle 2\) are vertical angles. Your job is to prove that \(\angle 1\cong \angle 2\). You can use any style of proof you prefer. Here is a two-column proof.
|
Statements |
Reasons |
|
\(m\angle 1+m\angle 3=180^{\circ}\) and \(m\angle 2+m\angle 3=180^{\circ}\) |
Two angles that form a line are supplementary |
| \(m\angle 1+m\angle 3=m\angle 2+m\angle 3\) |
Algebraic substitution |
| \(m\angle 1=m\angle 2\) |
Subtraction property of equality |
| \(\angle 1\cong \angle 2\) |
If two angles have the same measure, they are congruent. |
Vertical angles are congruent is a theorem. Now that it has been proven, you can use it in future proofs without proving it again.
2. When two parallel lines are cut by a transversal, two pairs of alternate interior angles are formed. In the diagram below, \(\angle 3\) and \(\angle 5\) are alternate interior angles. Similarly, \(\angle 4\) and \(\angle 6\) are alternate interior angles.
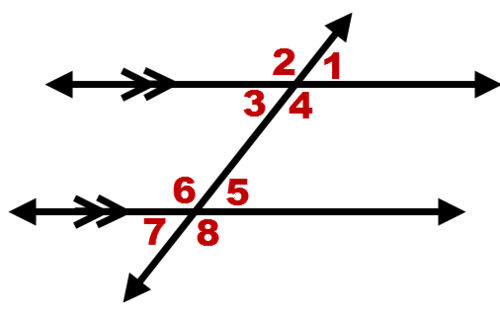
Prove that if two parallel lines are cut by a transversal, alternate interior angles are congruent.
Use the diagram above, and prove that \(\angle 3\cong \angle 5\). (The same exact proof would show that \(\angle 4\cong \angle 6\)). Again, in general you can use any style of proof that you prefer. Here is a paragraph proof.
\(\angle 1\cong \angle 3\) because they are vertical angles and vertical angles are always congruent. \(\angle 1\cong \angle 5\) because they are corresponding angles created by parallel lines and corresponding angles are congruent when lines are parallel. \(\angle 3\cong \angle 5\) because if two angles are congruent to the same angle, they are congruent to each other by the transitive property.
*Note: The transitive property states that if two objects are equal/congruent to the same third object, then they are equal/congruent to each other. The transitive property is a form of substitution. You can use it in any proof.
3. The statement “if two parallel lines are cut by a transversal, then alternate interior angles are congruent” is a theorem. Now that it has been proven, you can use it in future proofs without proving it again.
Prove that points on the perpendicular bisector of a line segment are equidistant from the endpoints of the line segment.
Start by exploring this claim. Draw a picture of a line segment and a perpendicular bisector of this segment. Remember that a perpendicular bisector is perpendicular to the line segment (meets it at a right angle) and bisects the line segment (cuts it in half).
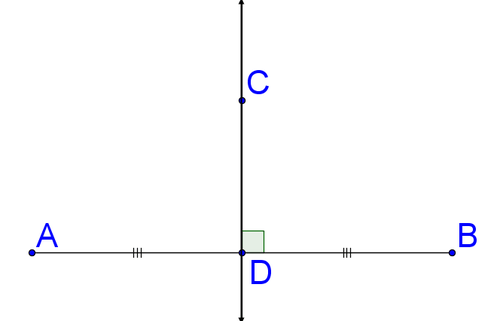
The claim is that any point on the perpendicular bisector (such as point \(C\)), is the same distance away from each endpoint. In other words, the claim is that for some generic point \(C\) on the perpendicular bisector, \(\overline{AC}\cong \overline{BC}\).
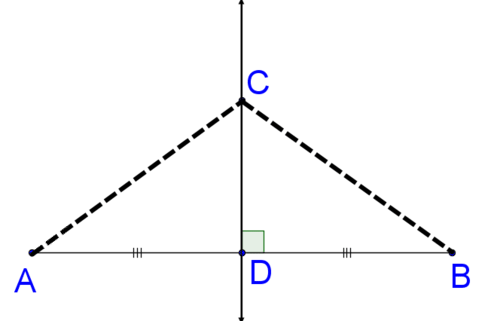
To prove the original statement, it will suffice to prove that if \(\overleftrightarrow{CD}\) is the perpendicular bisector to \(\overline{AB}\) with \(D\) on \(\overline{AB}\), then \(\overline{AC}\cong \overline{BC}\) using the above diagram as a reference. Remember, in general you can use any style of proof that you prefer. Here is a flow diagram. To prove this statement, you will show that the two triangles are congruent and then that the \(\overline{AC}\) and \(\overline{BC}\) are corresponding parts so must be congruent.
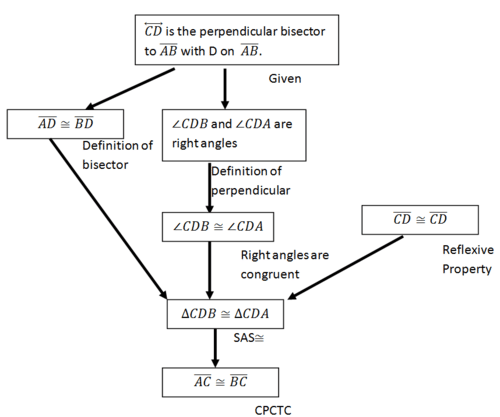
The statement “points on a perpendicular bisector of a line segment are equidistant from the segment's endpoints” is a theorem. Now that it has been proven, you can use it in future proofs without proving it again.
Example \(\PageIndex{1}\)
Earlier, you were asked how many lines exist that are parallel to l and pass through point \(P\).

Solution
Common sense should tell you that there is only one line through \(P\) that is parallel to \(l\).
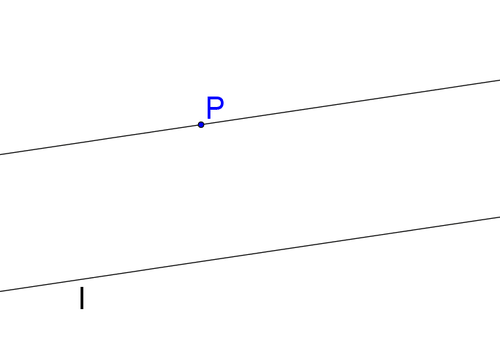
Interestingly, for hundreds of years people have attempted to prove this statement from simpler statements with no luck. Eventually, it was accepted that it simply must be a postulate, a statement that is assumed to be true without proof. This is known as the parallel postulate.
Example \(\PageIndex{2}\)
If corresponding angles are congruent, then are lines parallel?
Solution
This is known as the converse of the corresponding angles postulate. The original postulate said:
Original: If lines are parallel, then corresponding angles are congruent.
Here, the “if” part of the statement (known as the hypothesis) is switched with the “then” part of the statement (known as the conclusion).
Converse: If corresponding angles are congruent, then lines are parallel.
In general, just because a statement is true doesn't necessarily mean its converse is true. In this case, the converse does happen to be true. The only way for corresponding angles to be congruent is for the lines to be parallel. The corresponding angles converse is also a postulate, which means it is accepted as true without proof.
Example \(\PageIndex{3}\)
Prove that if lines are parallel, then same side interior angles (such as \(\angle 3\) and \(\angle 6\)) are supplementary.
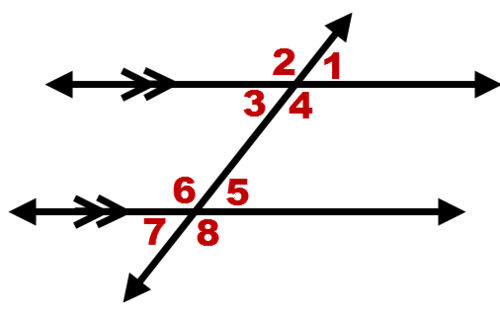
Solution
In general you can use any style of proof that you prefer. Here, use a paragraph proof.
\(\angle 3\cong \angle 5\) because they are alternate interior angles created by parallel lines and alternate interior angles are congruent when lines are parallel. \(m\angle 3=m\angle 5\) because congruent angles have the same measure. \(m\angle 5+m\angle 6=180^{\circ}\) because two angles that form a line are supplementary. By substitution, \(m\angle 3+m\angle 6=180^{\circ}\). \(\angle 3\) and \(\angle 6\) are supplementary because two angles with measures that add to \(180^{\circ}\) are supplementary.
The statement “if two parallel lines are cut by a transversal, then same side interior angles are supplementary” is a theorem. Now that it has been proven, you can use it in future proofs without proving it again.
Example \(\PageIndex{4}\)
Prove that if alternate interior angles are congruent, then lines are parallel.
Solution
This is the converse of the alternate interior angles theorem.
Original: If lines are parallel, then alternate interior angles are congruent.
Here, the “if” part of the statement (known as the hypothesis) is switched with the “then” part of the statement (known as the conclusion).
Converse: If alternate interior angles are congruent, then lines are parallel.
To prove this statement, start with a picture of alternate interior angles that are assumed to be congruent, but don't assume the lines are parallel. In the picture below, assume \(\angle 1\cong \angle 2\). Prove that \(m \parallel n\) (two parallel bars indicate parallel lines).
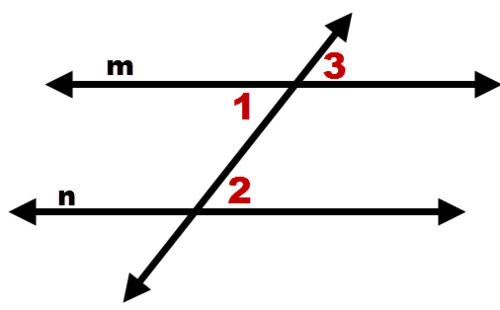
|
Statements |
Reasons |
| \(\angle 1\cong \angle 2\) |
Given |
| \(\angle 1\cong \angle 3\) |
Vertical angles are congruent |
| \(\angle 2\cong \angle 3\) |
Transitive property of congruence |
| \(m \parallel n\) |
If corresponding angles are congruent then lines are parallel. |
Review
1. In problem 1 from the Line and Angle Theorems section above, the theorem “vertical angles are congruent” was proved with a two-column proof. Rewrite this proof in a paragraph format.
2. In problem 2 from the Line and Angle Theorems section above, the theorem “if lines are parallel then alternate interior angles are congruent” was proved with a paragraph proof. Rewrite this proof with a flow diagram.
3. In problem 3 from the Line and Angle Theorems section above, the theorem “points on a perpendicular bisector of a line segment are equidistant from the segment's endpoints” was proved with a flow diagram. Rewrite this proof in a two-column format.
4. In Example 3, the theorem “if lines are parallel then same side interior angles are supplementary” was proved with a paragraph proof. Rewrite this proof in a two-column format.
5. In Example 4, the theorem “if alternate interior angles are congruent then lines are parallel” was proved with a two-column proof. Rewrite this proof with a flow diagram.
6. Alternate exterior angles are outside a pair of lines and on opposite sides of a transversal. \(\angle 2\) and \(\angle 8\) are an example of alternate exterior angles. \angle 1 and \angle 7 are another example of alternate exterior angles.
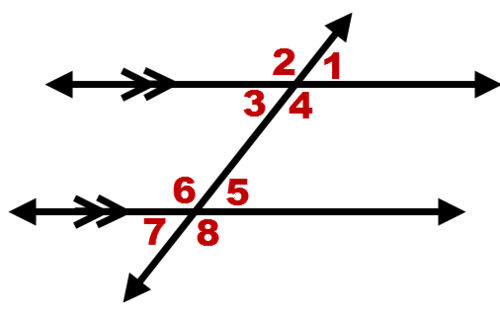
The theorem “if lines are parallel then alternate exterior angles are congruent” is partially proved below. Fill in the blanks to complete the proof. Note, the angles referenced are from the above picture.
|
Statements |
Reasons |
|
Two parallel lines are cut by a transversal |
_________ |
| \(\angle 2\cong \angle 6\) |
_________ |
| \(\angle 6\cong \underline{\qquad}\) |
Vertical angles are congruent. |
| _________ |
Transitive property. |
7. What is the converse of the theorem “if lines are parallel, then same side interior angles are supplementary”?
8. Prove the converse that you wrote in #7. Use any style of proof you prefer.
9. In problem 3 from the Line and Angle Theorems section above, the theorem “points on a perpendicular bisector of a line segment are equidistant from the segment's endpoints” was proved. This theorem could be rewritten as “if a point is on the perpendicular bisector of a line segment, then the point is equidistant from the endpoints of the line segment”. What is the converse of this theorem? To check your answer, look at #10.
10. The converse of the theorem in #9 is “if a point is equidistant from the endpoints of a line segment, then the point is on the perpendicular bisector of the line segment”. To prove this new theorem you can use the picture below.
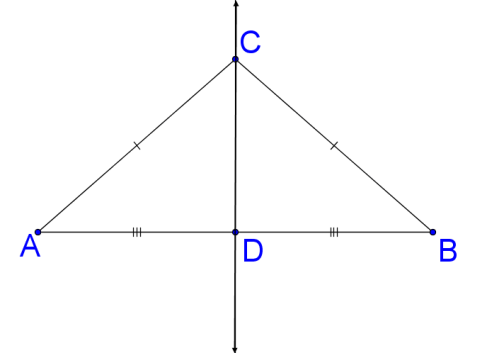
Assume point \(C\) is a random point that is equidistant from endpoints \(A\) and \(B\). Point \(D\) is the midpoint of line segment \(\overline{AB}\). Your goal is to show that \(\overline{CD}\) must be perpendicular to \(\overline{AB}\) (\(\overline{CD}\perp \overline{AB}\)). This new theorem is partially proved below. Fill in the blanks to complete the proof.
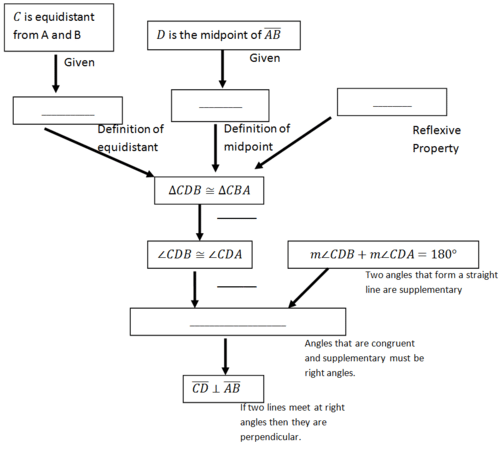
In 11-13, you will prove that if two angles are complementary to the same angle, then the two angles are congruent.
11. Draw a generic picture of this situation and label the three angles.
12. What are the “givens” from your picture? What are you trying to prove?
13. Write a proof of the statement using whatever proof style you prefer.
14. Using your work from 11-13 to help, prove that if two angles are supplementary to the same angle, then the two angles are congruent.
15. Give at least 3 methods for proving that lines are parallel.
Review (Answers)
To see the Review answers, open this PDF file and look for section 4.2.
Vocabulary
| Term | Definition |
|---|---|
| alternate interior angles | Alternate interior angles are two angles that are on the interior of two different lines, but on the opposite sides of the transversal. |
| Corresponding Angles | Corresponding angles are two angles that are in the same position with respect to the transversal, but on different lines. |
| perpendicular bisector | A perpendicular bisector of a line segment passes through the midpoint of the line segment and intersects the line segment at \(90^{\circ}\). |
| postulate | A postulate is a statement that is accepted as true without proof. |
| transversal | A transversal is a line that intersects two other lines. |
Additional Resources
Interactive Element

