2.17: Proofs Involving Triangles
- Page ID
- 7283
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Prove theorems about the sum of angles, base angles of isosceles triangles, and exterior and interior angles.
Theorems about Triangles
Recall that a triangle is a shape with exactly three sides. Triangles can be classified by their sides and by their angles.
When classifying a triangle by its sides, you should look to see if any of the sides are the same length.
- If no sides are the same length, then it is a scalene triangle.
- If two sides are the same length, then it is an isosceles triangle.
- If all three sides are the same length, then it is an equilateral triangle.

When classifying a triangle by its angles, you should look at the size of the angles:
- If a triangle has a right angle, then it is a right triangle.
- If the measures of all angles in a triangle are less than \(90^{\circ}\), then it is an acute triangle.
- A special case of an acute triangle is when all three angles are equal. In that case, all three angles are 60 degrees, and they form an equiangular triangle.
- If the measure of one angle in a triangle is greater than \(90^{\circ}\), then it is an obtuse triangle.

Triangle Sum Theorem
Prove that the interior angles of a triangle sum to \(180^{\circ}\).
This is a property of triangles that you have heard of and used before, but you may not have ever seen a proof for why it is true. Here is a paragraph format proof that relies on parallel lines and alternate interior angles.
Consider the generic triangle below.
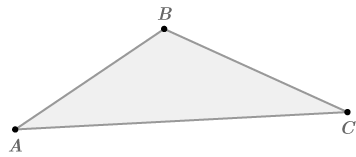
By the parallel postulate, there exists exactly one line parallel to \overline{AC}\) through B\). Draw this line.

\( \angle DBA\cong \angle A because they are alternate interior angles and alternate interior angles are congruent when lines are parallel. Therefore, \(m\angle DBA=m\angle A\). Similarly, \(\angle EBC\cong \angle C\) because they are also alternate interior angles, and so \(m\angle EBC=m\angle \). \(m\angle DBA+m\angle ABC+m\angle EBC=180^{\circ}\) because these three angles form a straight line. By substitution, \(m\angle A+m\angle ABC+m\angle C=180^{\circ}\).

The statement "the sum of the measures of the interior angles of a triangle is \(180^{\circ}\)" is known as the Triangle Sum Theorem. Now that it has been proven, you can use it in future proofs without proving it again.
Click the small blue arrow next to the image below and then drag the orange vertices to reshape the triangle. Observe that the sum of the measures of the interior angles of a triangle is always \(180^{\circ}\).

Isosceles Triangle Theorem
Prove that the base angles of an isosceles triangle are congruent.
The base angles of an isosceles triangle are the angles opposite the congruent sides. Below, the base angles are marked for isosceles \(\Delta ABC\).

You need to prove that \(\angle B\cong \angle C\) given that \(\overline{AB}\cong \overline{AC}\). Here is a proof in the two-column format, that relies on angle bisectors and congruent triangles. The proof will reference the picture below.

|
Statements |
Reasons |
|
Isosceles \(\Delta ABC\) |
Given |
| \(\overline{AB}\cong \overline{AC}\) |
Definition of isosceles triangle |
|
Construct \(\overrightleftarrow{AD}\), the angle bisector of \(\angle A\), with \(F\) the intersection of \(\overline{BC}\) and \(\overrightleftarrow{AD}\) |
An angle has only one angle bisector |
| \(\overline{AF}\cong \overline{AF}\) |
Reflexive Property |
| \(\angle BAF\cong \angle CAF\) |
Definition of angle bisector |
|
\(\Delta ABF\cong \Delta ACF\) |
\(SAS\cong\) |
| \(\angle B\cong \angle C\) |
\(CPCTC\) |
The statement "the base angles of an isosceles triangle are congruent" is the Isosceles Triangle Theorem. Now that it has been proven, you can use it in future proofs without proving it again.
Click the small blue arrow next to the image below and then drag the orange vertices to reshape the triangle. Observe that the base angles of an isosceles triangle are always congruent.

Interactive Element
Add interactive element text here. This box will NOT print up in pdfs
Exterior Angles Theorem
Prove that the measure of an exterior angle of a triangle is equal to the sum of the measures of the remote interior angles.
An exterior angle of a triangle is an angle outside of a triangle created by extending one of the sides of the triangles. Below, \(\angle ACD\) is an exterior angle. For exterior angle \(\angle ACD\), the angles \(\angle A\) and \(\angle B\) are the remote interior angles, because they are the interior angles that are not adjacent to the exterior angle.

Here is a flow diagram proof of this theorem.
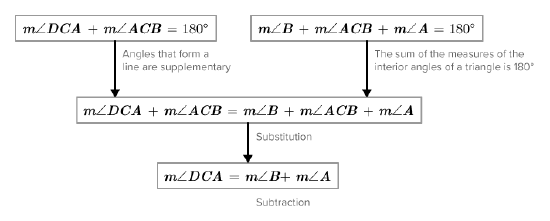
The statement "the measure of an exterior angle of a triangle is equal to the sum of the measures of the remote interior angles" is the Exterior Angles Theorem. Now that it has been proven, you can use it in future proofs without proving it again.
Click the small blue arrow next to the image below and then drag the orange vertices to reshape the triangle. Choose two remote interior angles of the triangle and observe how measure of an exterior angle remains equal to the sum of the remote interior angles.

In the interactive below, move the red points to change the shape of the triangle. Move the blue points to compare angles \angle 1\), \angle 2\), and \angle 3\).
Notice that because they are vertical angles, the angle pairs \(m\angle 1=m\angle 4\), \(m\angle 2=m\angle 5\), and \(m\angle 3=m\angle 6\).
Interactive Element
Add interactive element text here. This box will NOT print up in pdfs
Triangle Midsegment Theorem
In the triangle below, point D is a midpoint of \(\overline{AC}\) and point \(E\) is the midpoint of \(\overline{BC}\). Make a conjecture about how \(\overline{DE}\) relates to \(\overline{AB}\).

A conjecture is a guess about something that might be true. After making a conjecture, usually you will try to prove it. Two possible conjectures are:
- \(\overline{DE} \parallel \overline{AB}\)
- The length of \(\overline{DE}\) is half the length of \(\overline{AB}\)
Consider the picture below.

To prove the conjecture \(DE\parallel AB, we need to prove that \(\Delta FEB\cong \Delta DEC which we then use to prove that \(BF\parallel AC. We then continue with the proof to prove that \(\Delta ADB\cong \Delta FBD which then leads us to prove that \(DE\parallel AB.
|
Statements |
Reasons |
|
|
1. |
\(\overline{DC}\cong \overline{AD}\), \(\overline{CE}\cong \overline{EB}\), \(\overline{DE}\cong \overline{EF}\) |
Given |
| \(\angle CED\cong \angle FEB\) |
Vertical angles are congruent |
|
| \(\Delta FEB\cong \Delta DEC\) | \(SAS\cong\) | |
|
2. |
\(\angle FBE\cong \angle ECD\) |
\(CPCTC\) |
| \(\overline{BF} \parallel \overline{AC}\) |
If alternate interior angles are congruent then lines are parallel. |
|
|
3. |
\(\angle ADB\cong \angle DBF\) |
If lines are parallel then alternate interior angles are congruent. |
| \(\overline{DB}\cong \overline{DB}\) |
Reflexive property |
|
| \(\overline{BF}\cong \overline{DC}\) |
\(CPCTC\) |
|
| \(\overline{BF}\cong \overline{AD}\) |
Substitution |
|
| \(\Delta ADB\cong \Delta FBD\) | \(SAS\cong\) | |
|
4. |
\(\angle ABD\cong \angle FDB\) |
\(CPCTC\) |
| \(\overline{DE} \parallel \overline{AB}\) |
If alternate interior angles are congruent then lines are parallel. |
Here is the figure again, for reference:

Now prove the conjecture that the length of \(DE is half the length of \(AB\).
| Statements | Reasons | |
| 5. | \(\overline{DF}\parallel \overline{AB}\) | \(\overline{DE}\) produced at \(F\) |
| \(\overline{BF}\parallel \overline{AD}\) | \(D\) is a midpoint of \(AC\) | |
| \(ABFD\) is a parallelogram | Definition of a parallelogram | |
| \(\overline{DE}=\dfrac{1}{2} \overline{DF}\) | \(\overline{DE}\cong \overline{EF}\) | |
| \(\overline{DE}=\dfrac{1}{2} \overline{AB}\) | Definition of a parallelogram |
Thus, the line segment joining the midpoints of any two sides of a triangles is parallel to the third side and equal to half of it, this is the Triangle Midsegment Theorem. Note that there are other ways to prove that the two segments are parallel. One method relies on similar triangles, which will be explored in another concept.
Click on the small blue arrow next to the image below and then drag the orange vertices to reshape the triangle. Observe that the line segment joining the mid-points of the two sides of a triangle is parallel to the third side and equal to half of it.

CK-12 PLIX Interactive
Interactive Element
Review
1. Earlier, you proved that the sum of the interior angles of a triangle is \(180^{\circ}\) (the triangle sum theorem) using a paragraph proof. Now, rewrite this proof in the two-column format.
2. Rewrite the proof of the Triangle Sum Theorem again, this time in the flow diagram format.
3. Earlier, you proved that the base angles of an isosceles triangle are congruent using a two-column proof. Now, rewrite this proof in the paragraph format.
4. Rewrite the isosceles triangle theorem again, this time in the flow diagram format.
5. Earlier, you proved that the measure of an exterior angle of a triangle is equal to the sum of the measures of the remote interior angles using the flow diagram format. Now, rewrite this proof in the paragraph format.
6. Rewrite the exterior angles proof again, this time in the two-column format.
7. Recall that the segment joining midpoints of two sides of a triangle is parallel to the third side of the triangle. Given the diagram below and that \(\Delta ADB\cong \Delta FBD\) as proved earlier in the lesson, prove that \(DE=\dfrac{1}{2} AB\).
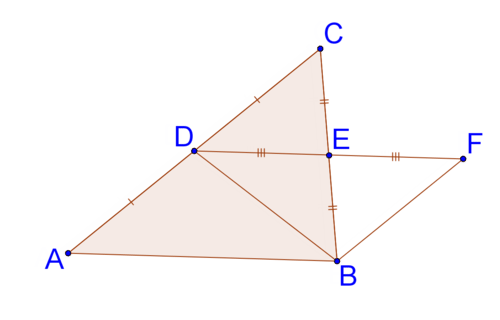
8. What is the converse of: "if a triangle is isosceles, the base angles are congruent?" Why do you think the converse is also true or is not true?
9. Prove that if two angles of a triangle are congruent, then the triangle is isosceles. Use the diagram and two-column proof below and fill in the blanks to complete the proof.
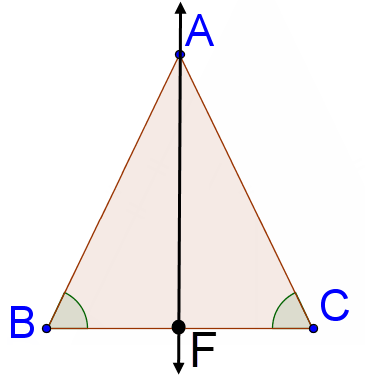
|
Statements |
Reasons |
| \(\angle B\cong \angle C\) |
________ |
|
Construct \(\overrightleftarrow{AF}\), the angle bisector of \(\angle A\), with \(F\) the intersection of \(\overline{BC}\) and \(\overrightleftarrow{AF}\) |
An angle has only one angle bisector |
| ________ |
Definition of angle bisector |
|
________ |
Reflexive Property |
| \(\Delta ABF\cong \Delta ACF\) | ________ |
| ________ |
\(CPCTC\) |
10. Rewrite the proof that a triangle with two congruent angles is isosceles in the flow diagram format.
11. Rewrite the isosceles triangle proof in the paragraph format.
12. Given that \(\Delta ABC\cong \Delta BAD\), prove that \(\Delta AEB\) is isosceles.
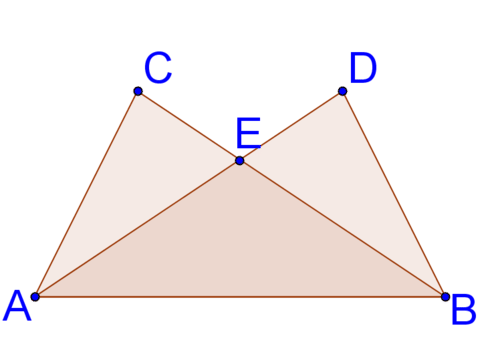
13. Given the markings in the picture below, explain why \(\overline{CD}\) is the perpendicular bisector of \(\overline{AB}\).
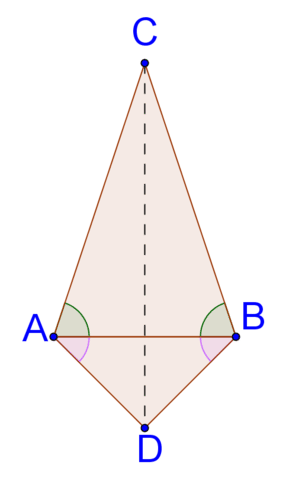
14. In the picture below, \(\Delta ABC is isosceles with \(\overline{AC}\cong \overline{CB}\). \(E\) is the midpoint of \(\overline{AC}\) and \(D\) is the midpoint of \(\overline{CB}\). Prove that \(\Delta EAB\cong \Delta DBA\).
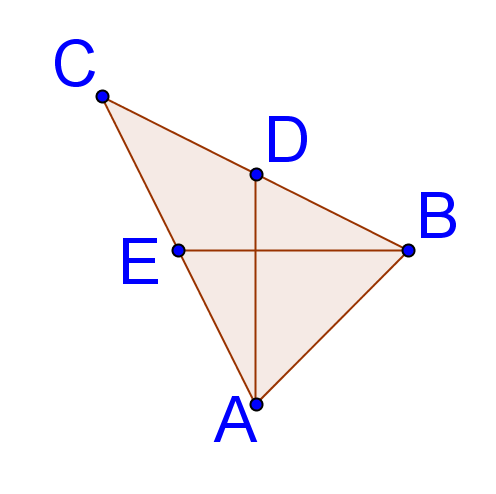
15. Explain why knowing that \(\DeltaABC\) is isosceles is not enough information to prove that \(\DeltaABD\cong \DeltaCBD\).
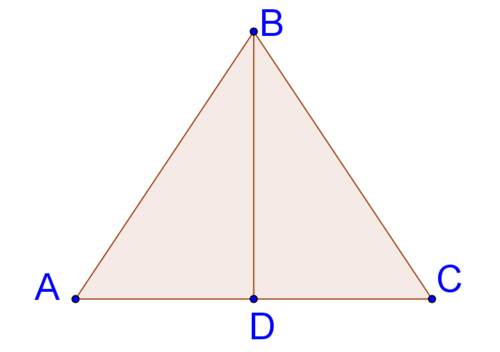
16 Given: \(\angle CBD\cong \angle EFD\); \(\overline{CB}\cong \overline{EF}\)
Prove: \(\angle DBF\cong \angle DFB\)

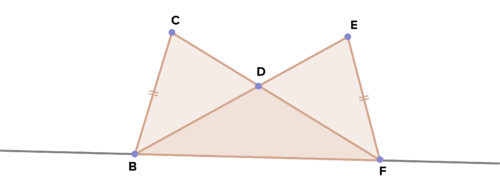
17. Given: \(\overline{BC}\cong \overline{EF}\); \(\overline{CF}\cong \overline{EB}\)
Prove: \(\Delta BDF\) is isosceles
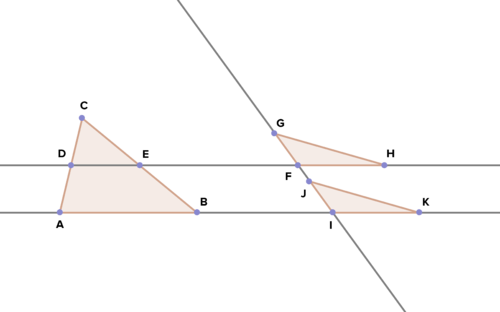
18. Given: \(\overline{DE}\) midsegment of \(\Delta ABC \); \(\overline{GF}\cong \overline{JI}\); \(\overline{FH}\cong \overline{IK}\)
Prove: \(\Delta GFH \cong \Delta JIK\)
Review (Answers)
To see the Review answers, click here.
Additional Resources
Interactive Element
Practice: Proofs Involving Triangles

