4.1.10: Applications of the Law of Cosines
- Page ID
- 14874
Relationship between the three sides and an angle for non-right triangles.
While helping your mom bake one day, the two of you get an unusual idea. You want to cut the cake into pieces, and then frost over the surface of each piece. You start by cutting out a slice of the cake, but you don't quite cut the slice correctly. It ends up being an oblique triangle, with a 5 inch side, a 6 inch side, and an angle of \(70^{\circ} \) between the sides you measured. Can you help your mom determine the length of the third side, so she can figure out how much frosting to put out?
Law of Cosines
The Law of Cosines is a fantastic extension of the Pythagorean Theorem to oblique triangles. In this section, we show some interesting ways to utilize this formula to analyze real world situations.
Let's take a look at a few problems where we use the Law of Cosines.
1. In a game of pool, a player must put the eight ball into the bottom left pocket of the table. Currently, the eight ball is 6.8 feet away from the bottom left pocket. However, due to the position of the cue ball, she must bank the shot off of the right side bumper. If the eight ball is 2.1 feet away from the spot on the bumper she needs to hit and forms a \(168^{\circ} \) angle with the pocket and the spot on the bumper, at what angle does the ball need to leave the bumper?
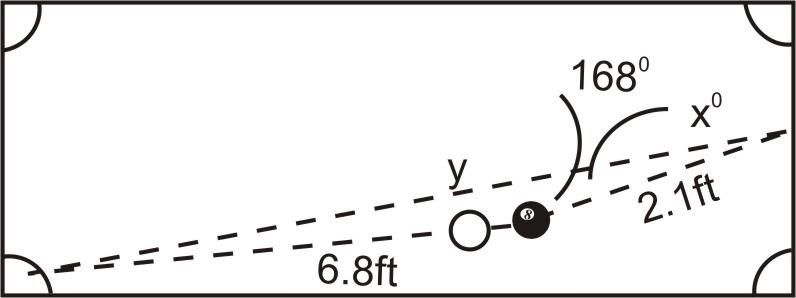
Note: This is actually a trick shot performed by spinning the eight ball, and the eight ball will not actually travel in straight-line trajectories. However, to simplify the problem, assume that it travels in straight lines.
In the scenario above, we have the SAS case, which means that we need to use the Law of Cosines to begin solving this problem. The Law of Cosines will allow us to find the distance from the spot on the bumper to the pocket (y). Once we know y, we can use the Law of Sines to find the angle (X).
\(\begin{aligned} y^2 &=6.8^2+2.1^2−2(6.8)(2.1) \cos 168^{\circ} \\ y^2 &=78.59\\ y&=8.86 \text{ feet} \end{aligned}\)
2. The distance from the spot on the bumper to the pocket is 8.86 feet. We can now use this distance and the Law of Sines to find angle X. Since we are finding an angle, we are faced with the SSA case, which means we could have no solution, one solution, or two solutions. However, since we know all three sides this problem will yield only one solution.
\(\begin{aligned}
\dfrac{\sin 168^{\circ}}{8.86} &=\dfrac{\sin X}{6.8} \\
\dfrac{6.8 \sin 168^{\circ}}{8.86} &=\sin X \\
0.1596 & \approx \sin B \\
\angle B &=8.77^{\circ}
\end{aligned}\)
In the previous example, we looked at how we can use the Law of Sines and the Law of Cosines together to solve a problem involving the SSA case. In this section, we will look at situations where we can use not only the Law of Sines and the Law of Cosines, but also the Pythagorean Theorem and trigonometric ratios. We will also look at another real-world application involving the SSA case.
3. Three scientists are out setting up equipment to gather data on a local mountain. Person 1 is 131.5 yards away from Person 2, who is 67.8 yards away from Person 3. Person 1 is 72.6 yards away from the mountain. The mountains forms a \(103^{\circ} \) angle with Person 1 and Person 3, while Person 2 forms a \(92.7^{\circ} \) angle with Person 1 and Person 3. Find the angle formed by Person 3 with Person 1 and the mountain.
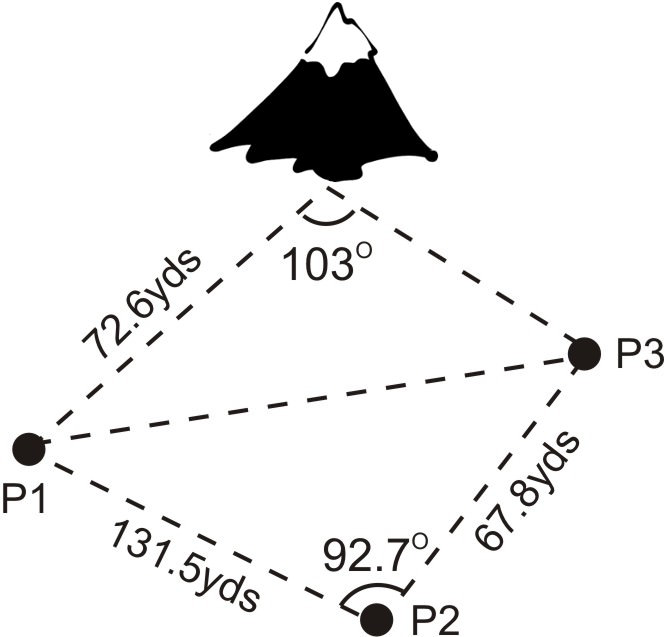
In the triangle formed by the three people, we know two sides and the included angle (SAS). We can use the Law of Cosines to find the remaining side of this triangle, which we will call x. Once we know x, we will two sides and the non-included angle (SSA) in the triangle formed by Person 1, Person 2, and the mountain. We will then be able to use the Law of Sines to calculate the angle formed by Person 3 with Person 1 and the mountain, which we will refer to as \(Y\).
To find \(x\):
\(\begin{aligned} x^2 &=131.5^2+67.8^2−2(131.5)(67.8)\cos 92.7\\ x^2 &=22729.06397\\ x&=150.8 \text{ yds} \end{aligned}\)
Now that we know \(x=150.8\), we can use the Law of Sines to find \(Y\). Since this is the SSA case, we need to check to see if we will have no solution, one solution, or two solutions. Since \(150.8>72.6\), we know that we will have only one solution to this problem.
\(\begin{aligned}
\dfrac{\sin 103}{150.8} &=\dfrac{\sin Y}{72.6} \\
\dfrac{72.6 \sin 103}{150.8} &=\sin Y \\
0.4690932805 &=\sin Y \\
28.0 & \approx \angle Y
\end{aligned}\)
4. Katie is constructing a kite shaped like a triangle.
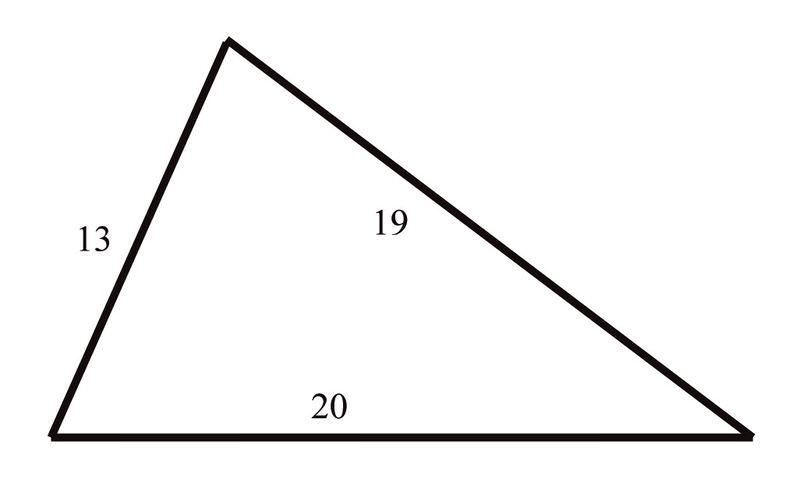
She knows that the lengths of the sides are a = 13 inches, b = 20 inches, and c = 19 inches. What is the measure of the angle between sides "\(a\)" and "\(b\)"?
Since she knows the length of each of the sides of the triangle, she can use the Law of Cosines to find the angle desired:
\(\begin{aligned}
c^{2} &=a^{2}+b^{2}-2(a)(b) \cos C \\
19^{2} &=13^{2}+20^{2}-(2)(13)(20) \cos C \\
361 &=169+400-520 \cos C \\
-208 &=-520 \cos C \\
\cos C &=0.4 \\
C &\approx 66.42^{\circ}
\end{aligned}\)
Earlier, you were asked to determine the length of the third side.
Solution
You can use the Law of Cosines to help your mom find out the length of the third side on the piece of cake:
\(\begin{aligned}
c^{2}&=a^{2}+b^{2}-2 a b \cos C \\
c^{2}&=5^{2}+6^{2}+(2)(5)(6) \cos 70^{\circ} \\
c^{2}&=25+36+60(.342) \\
c^{2}&=81.52 \\
c &\approx 9.03
\end{aligned}\)
The piece of cake is just a little over 9 inches long.
You are cutting a triangle out for school that looks like this:
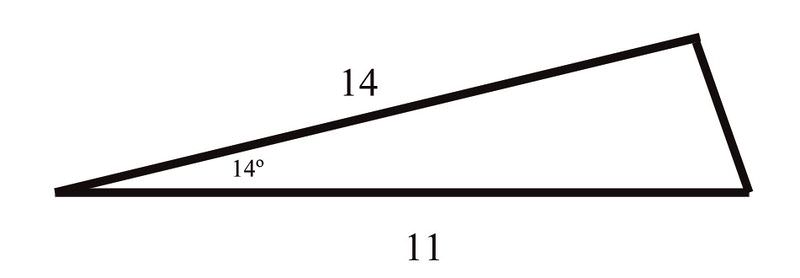
Find side \(c\) (which is the side opposite the \(14^{\circ} \) angle) and \(\angle B \)(which is the angle opposite the side that has a length of 14).
Solution
You know that two of the sides have lengths of 11 and 14 inches, and that the angle between them is \(14^{\circ} \). You can use this to find the length of the third side:
\(\begin{aligned}
c^{2}&=a^{2}+b^{2}-2 a b \cos \theta \\
c^{2}&=121+196-(2)(11)(14)(.97) \\
c^{2}&=121+196-307.384 \\
c^{2}&=9.16 \\
c&=3.03
\end{aligned}\)
And with this you can use the Law of Sines to solve for the unknown angle:
\(\begin{aligned}
\dfrac{\sin 14^{\circ}}{3.03}&=\dfrac{\sin B}{11} \\
\sin B&=\dfrac{11 \sin 14^{\circ}}{3.03} \\
\sin B&=.878 \\
B&=\sin ^{-1}(.0307)=61.43^{\circ}
\end{aligned}\)
While hiking one day you walk for 2 miles in one direction. You then turn \(110^{\circ} \) to the left and walk for 3 more miles. Your path looks like this:
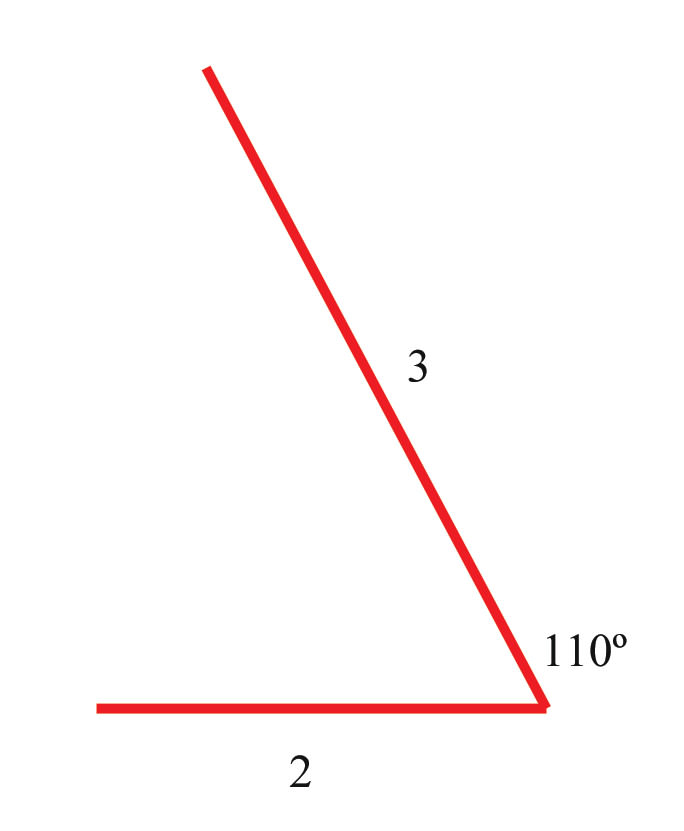
Solution
When you turn to the left again to complete the triangle that is your hiking path for the day, how far will you have to walk to complete the third side? What angle should you turn before you start walking back home?
Since you know the lengths of two of the legs of the triangle, along with the angle between them, you can use the Law of Cosines to find out how far you'll have to walk along the third leg:
\(\begin{aligned}
c^{2}&=a^{2}+b^{2}+2 a b \cos 70^{\circ} \\
c^{2}&=4+1+(2)(2)(1)(.342) \\
c^{2}&=6.368 \\
c&=\sqrt{6.368} \approx 2.52
\end{aligned}\)
Now you have enough information to solve for the interior angle of the triangle that is supplementary to the angle you need to turn:
\(\begin{aligned}
\dfrac{\sin A}{a}&=\dfrac{\sin B}{b} \\
\dfrac{\sin 70^{\circ}}{2.52}&=\dfrac{\sin B}{2} \\
\sin B&=\dfrac{2 \sin 70^{\circ}}{2.52}=\dfrac{1.879}{2.52}=.746 \\
B&=\sin ^{-1}(.746)=48.25^{\circ}
\end{aligned}\)
The angle \(48.25^{\circ} \) is the interior angle of the triangle. So you should turn \(90^{\circ} +(90^{\circ} −48.25^{\circ} )=90^{\circ} +41.75^{\circ} =131.75^{\circ} \) to the left before starting home.
A support at a construction site is being used to hold up a board so that it makes a triangle, like this:
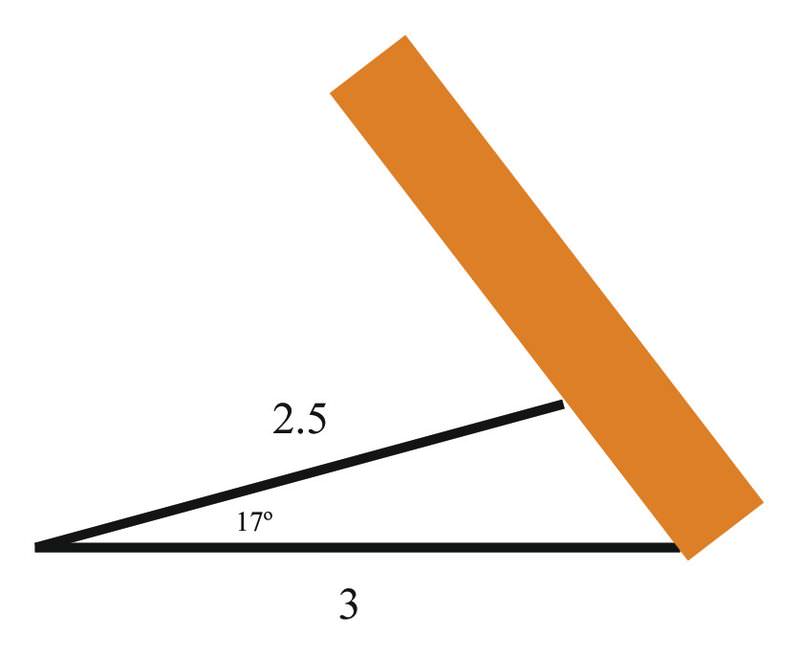
Solution
If the angle between the support and the ground is \(17^{\circ} \), the length of the support is 2.5 meters, and the distance between where the board touches the ground and the bottom of the support is 3 meters, how far along the board is the support touching? What is the angle between the board and the ground?
You should use the Law of Cosines first to solve for the distance from the ground to where the support meets the board:
\(\begin{aligned} c^2&=a^2+b^2+2ab \cos 17^{\circ} \\ c^2&=6.25+9+(2)(2.5)(3)\cos 17^{\circ} \\ c^2&=6.25+9+(2)(2.5)(3)(.956) \\ c^2&=26.722 \\ c&\approx 5.17 \end{aligned}\)
And now you can use the Law of Sines:
\(\begin{aligned}
\dfrac{\sin A}{a} &=\dfrac{\sin B}{b} \\
\dfrac{\sin 17^{\circ}}{5.17} &=\dfrac{\sin B}{2.5} \\
\sin B &=\dfrac{2.5 \sin 17^{\circ}}{5.17} =.1414 \\
B&=\sin ^{-1}(.1414) =8.129^{\circ}
\end{aligned}\)
Review
In \(\Delta ABC\), \(a=12\), \(b=15\), and \(c=20\).
- Find \(m\angle A\).
- Find \(m\angle B\).
- Find \(m\angle C\).
In \(\Delta DEF\), \(d=25\), \(e=13\), and \(f=16\).
- Find \(m\angle D\).
- Find \(m\angle E\).
- Find \(m\angle F\).
In \(\Delta KBP\), \(k=19\), \(\angle B=61^{\circ} \), and \(p=12\).
- Find the length of \(b\).
- Find \(m\angle K\).
- Find \(m\angle P\).
- While hiking one day you walk for 5 miles due east, then turn to the left and walk 3 more miles \(30^{\circ} \) west of north. At this point you want to return home. How far are you from home if you were to walk in a straight line?
- A parallelogram has sides of 20 and 31 ft, and an angle of \(46^{\circ} \). Find the length of the longer diagonal of the parallelogram.
- Dirk wants to find the length of a long building from one side (point \(A\)) to the other (point \(B\)). He stands outside of the building (at point \(C\)), where he is 500 ft from point \(A\) and 220 ft from point \(B\). The angle at \(C\) is \(94^{\circ} \). Find the length of the building.
Determine whether or not each triangle is possible.
- \(a=12\), \(b=15\), \(c=10\)
- \(a=1\), \(b=5\), \(c=4\)
- \(\angle A=32^{\circ}\), \(a=8\), \(b=10\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 5.11.
Vocabulary
| Term | Definition |
|---|---|
| Included Angle | The included angle in a triangle is the angle between two known sides. |
| law of cosines | The law of cosines is a rule relating the sides of a triangle to the cosine of one of its angles. The law of cosines states that \(c^2=a^2+b^2−2ab\cos C\), where \(C\) is the angle across from side \(c\). |
| SAS | SAS means side, angle, side, and refers to the fact that two sides and the included angle of a triangle are known. |
| SSS | SSS means side, side, side and refers to the fact that all three sides of a triangle are known in a problem. |
Additional Resources
Video: Solving triangles u\sin g the Law of Cosines - Example 1
Practice: Applications of the Law of Cosines