4.2.2: Introduction to the Triangle Area Formula

Last updated
Save as PDF

Page ID: 4169

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Find areas of non-right triangles using the sine ratio

While in the lunch room with your friends one day, you're discussing different ways you can use the things you've learned in math class. You tell your friends that you've been learning a lot about triangles, such as how to find their area. One of your friends looks down at your plate and starts to smile.

"Alright," he says. "If you're so good at things involving triangles, I dare you to find something simple. Tell me the area of your slice of pizza." He points down at the pizza on your plate.

The pizza is shaped like a triangle. But unfortunately its not a right triangle. The outer edge is 5 inches long, and the long sides are 7 inches long. The angle between the edge and the long side of the slice is $69^{\circ} $. Is there any way to tell the area of your pizza slice?

Deriving the Triangle Area Formula

We can use the area formula from Geometry, $A=\dfrac{1}{2} bh$, as well as the sine function, to derive a new formula that can be used when the height, or altitude, of a triangle is unknown.

In $\Delta ABC$ below, $BD$ is altitude from $B$ to $AC$. We will refer to the length of $BD$ as $h$ since it also represents the height of the triangle. Also, we will refer to the area of the triangle as $K$ to avoid confusing the area with $\angle A$.

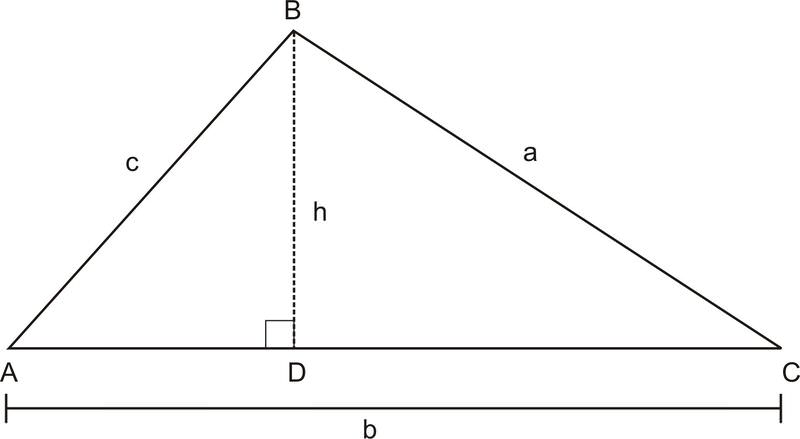
f-d_42d7a855c381b3d9878bd1c6a6d1e8f57e06e6f9b93aa11b50f7eab2+IMAGE_TINY+IMAGE_TINY.jpg — Figure $\PageIndex{1}$

$\begin{aligned} k &=\dfrac{1}{2} bh && \text{ Area of a triangle } \\ k&=\dfrac{1}{2} b(c \sin A) &&\sin A=\dfrac{h }{c} \text{ therefore } c \sin A=h \\ k&=\dfrac{1}{2} bc \sin A && \text{Simplify} \end{aligned}$

We can use a similar method to derive all three forms of the area formula, regardless of the angle:

$\begin{aligned} K &=\dfrac{1}{2} bc \sin A\\ K&=\dfrac{1}{2} ac \sin B \\ K&=\dfrac{1}{2} ab \sin C \end{aligned}$

The formula $K=\dfrac{1}{2} bc \sin A$ requires us to know two sides and the included angle (SAS) in a triangle. Once we know these three things, we can easily calculate the area of an oblique triangle.

Finding the Area of a Triangle

1. In $\Delta ABC$, $\angle C=62^{\circ} $, $b=23.9$, and $a=31.6$. Find the area of the triangle.

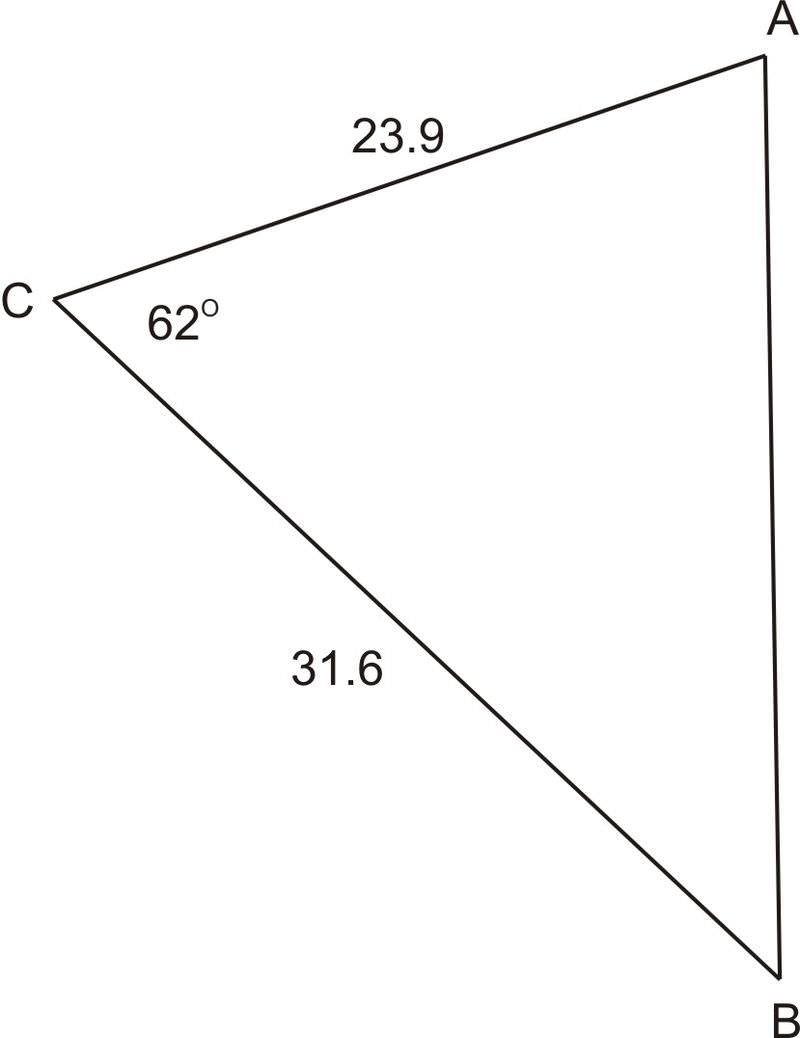
f-d_88085b60af7c63a417d5bf9307251544924079b3a50310773ca46bc2+IMAGE_TINY+IMAGE_TINY.jpg — Figure $\PageIndex{2}$

Using our new formula, $K=\dfrac{1}{2} ab\sin C$, plug in what is known and solve for the area.

$\begin{aligned} K &=\dfrac{1}{2}(31.6)(23.9)\sin 62 \\ K &\approx 333.4 \end{aligned}$

2. The Pyramid Hotel recently installed a triangular pool. One side of the pool is 24 feet, another side is 26 feet, and the angle in between the two sides is $87^{\circ} $. If the hotel manager needs to order a cover for the pool, and the cost is $$35$ per square foot, how much can he expect to spend?

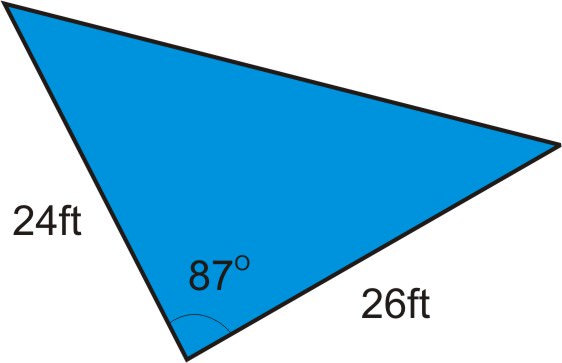
f-d_b225b9b5ef58bb0ea297cd99282e794acb720c559d7f7a4a019fef4a+IMAGE_TINY+IMAGE_TINY.jpg — Figure $\PageIndex{3}$

In order to find the cost of the cover, we first need to know the area of the cover. Once we know how many square feet the cover is, we can calculate the cost. In the illustration above, you can see that we know two of the sides and the included angle. This means we can use the formula $K=\dfrac{1}{2} bc \sin A$.

$\begin{aligned} K&=\dfrac{1}{2} (24)(26)\sin 87 \\ K&\approx 311.6 \\ 311.6 \text{ sq.ft.} \times $35/ \text{ sq.ft. }&=$10,905.03 \end{aligned}$

The cost of the cover will be $$10,905.03$.

3. In $\Delta GHI$, $\angle I=15^{\circ} $, $g=14.2$, and $h=7.9$. Find the area of the triangle.

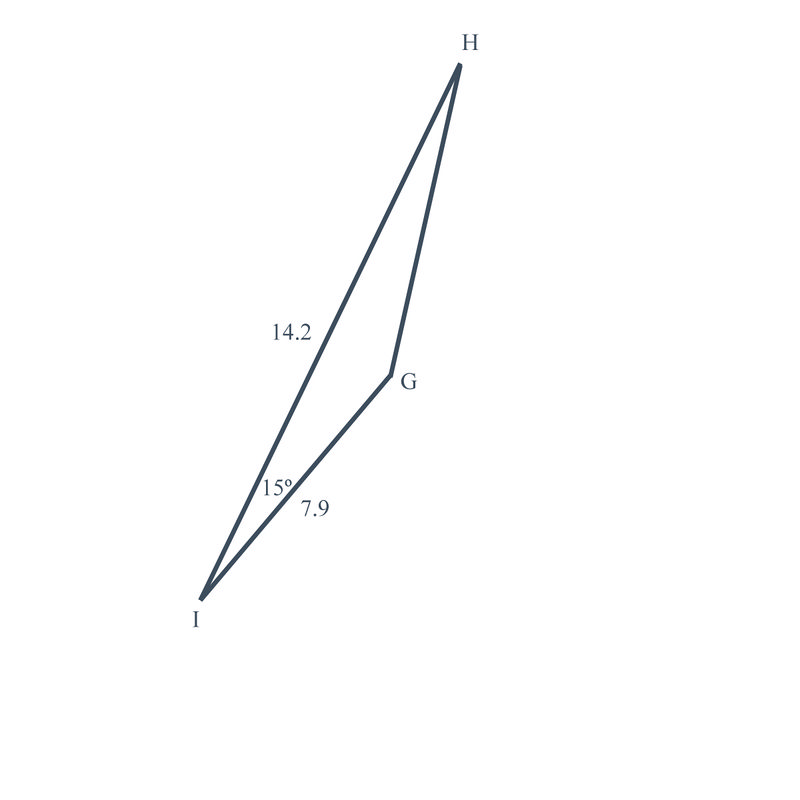
f-d_3ffcc6a0440af3b81b09674fe833f939dc9c38e1bcb89c8c54711c7e+IMAGE_TINY+IMAGE_TINY.jpg — Figure $\PageIndex{4}$

Using our new formula, $K=\dfrac{1}{2} ab \sin C$, which is the same as $K=\dfrac{1}{2} gh \sin I$, plug in what is known and solve for the area.

$\begin{aligned} K &=\dfrac{1}{2} (14.2)(7.9)\sin 15 \\ K&\approx 14.52\end{aligned} $

Example $\PageIndex{1}$

Earlier, you were asked if there was any way to tell the area of your pizza slice.

Solution

Use the formula $K=\dfrac{1}{2} bc \sin A$

where in this case, one of the sides is equal to 5, the other is equal to 7, and the angle is $69^{\circ} $.

$K=\dfrac{1}{2} (5)(7) \sin 69^{\circ} =16.34\text{ in}^2$

Example $\PageIndex{2}$

A farmer needs to replant a triangular section of crops that died unexpectedly. One side of the triangle measures 186 yards, another measures 205 yards, and the angle formed by these two sides is $148^{\circ} $.

What is the area of the section of crops that needs to be replanted?

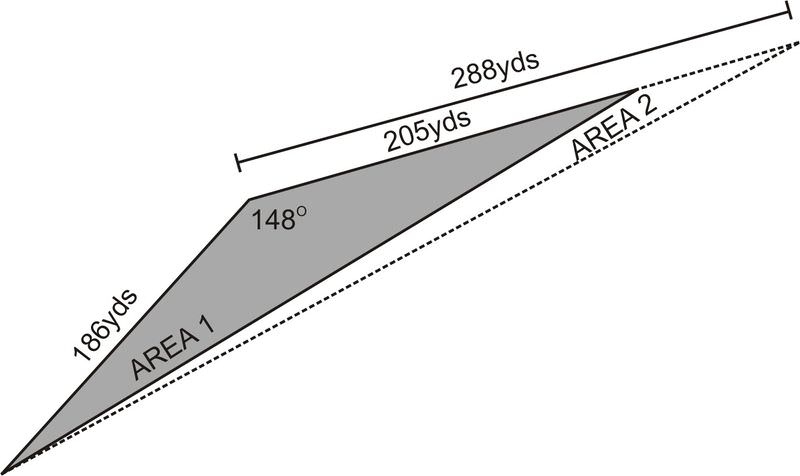
f-d_a8dfba8c71ba1787b6ae107fe60fdd721611a2bf2ab402106f4db2a0+IMAGE_TINY+IMAGE_TINY.jpg — Figure $\PageIndex{5}$

Solution

Use $K=\dfrac{1}{2} bc \sin A$, $K=\dfrac{1}{2} (186)(205)\sin 148^{\circ} $. So, the area that needs to be replaced is 10102.9 square yards.

Example $\PageIndex{3}$

The farmer goes out a few days later to discover that more crops have died. The side that used to measure 205 yards now measures 288 yards. How much has the area that needs to be replanted increased by?

Solution

$K=\dfrac{1}{2}(186)(288)\sin 148^{\circ} =14193.4$, the area has increased by 4090.5 yards.

Example $\PageIndex{4}$

Find the perimeter of the quadrilateral at the left If the area of $\Delta DEG=56.5$ and the area of $\Delta EGF=84.7$.

Solution

You need to use the $K=\dfrac{1}{2} bc \sin A$ formula to find DE and GF.

$56.5=\dfrac{1}{2} (13.6)DE \sin 39^{\circ} \rightarrow DE=13.2 \qquad 84.7=\dfrac{1}{2}(13.6)EF \sin 60^{\circ} \rightarrow EF=14.4$

Second, you need to find sides $DG$ and $GF$ using the Law of Cosines.

$\begin{aligned} DG^2 & =13.2^2+13.6^2−2\cdot 13.2\cdot 13.6\cdot \cos 39^{\circ} \rightarrow DG=8.95 \\ GF^2 &=14.4^2+13.6^2−2\cdot 14.4\cdot 13.6\cdot \cos 60^{\circ} \rightarrow GF=14.0 \end{aligned} $

The perimeter of the quadrilateral is 50.55.

Review

Find the area of each triangle.

$\Delta ABC$ if $a=13$, $b=15$, and $m\angle C=71^{\circ} $.
$\Delta ABC$ if $b=8$, $c=4$, and $m\angle A=67^{\circ} $.
$\Delta ABC$ if $b=34$, $c=29$, and $m\angle A=138^{\circ} $.
$\Delta ABC$ if $a=3$, $b=7$, and $m\angle C=80^{\circ} $.
$\Delta ABC$ if $a=4.8$, $c=3.7$, and $m\angle B=43^{\circ} $.
$\Delta ABC$ if $a=12$, $b=5$, and $m\angle C=20^{\circ} $.
$\Delta ABC$ if $a=3$, $b=10$, and $m\angle C=50^{\circ} $.
$\Delta ABC$ if $a=5$, $b=9$, and $m\angle C=14^{\circ} $.
$\Delta ABC$ if $a=5$, $b=7$, and $c=11$.
$\Delta ABC$ if $a=7$, $b=8$, and $c=9$.
$\Delta ABC$ if $a=12$, $b=14$, and $c=4$.
A farmer measures the three sides of a triangular field and gets 114, 165, and 257 feet. What is the measure of the largest angle of the triangle?
Using the information from the previous problem, what is the area of the field?

Another field is a quadrilateral where three sides measure 30, 50, and 60 yards, and two angles measure $130^{\circ} $ and $140^{\circ} $, as shown below.

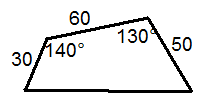
f-d_686023e1dff58d9f6cacb3b2c1002a196d1f535b99c211625971352f+IMAGE_TINY+IMAGE_TINY.png — Figure $\PageIndex{6}$

Find the area of the quadrilateral. Hint: divide the quadrilateral into two triangles and find the area of each.
Find the length of the fourth side.
Find the measures of the other two angles.

Review (Answers)

To see the Review answers, open this PDF file and look for section 5.4.

Vocabulary

Term	Definition
Oblique Triangle	An oblique triangle is a triangle without a right angle as one of its internal angles.
SAS Triangle	An SAS triangle is a triangle where two sides and the angle in between them are known quantities.