7.15: Dilation of a Shape
- Page ID
- 5920
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Larger or smaller version of a figure that preserves its shape.
Dilation
Two figures are similar if they are the same shape but not necessarily the same size. One way to create similar figures is by dilating. A dilation makes a figure larger or smaller but the new resulting figure has the same shape as the original.
Dilation: An enlargement or reduction of a figure that preserves shape but not size. All dilations are similar to the original figure.
Dilations have a center and a scale factor. The center is the point of reference for the dilation and the scale factor tells us how much the figure stretches or shrinks. A scale factor is labeled \(k\). Only positive scale factors, \(k\), will be considered in this text.
If the dilated image is smaller than the original, then \(0<k<1\).
If the dilated image is larger than the original, then \(k>1\).
A dilation, or image, is always followed by a \(′\).
| Label It | Say It |
|---|---|
| \(′\) | “prime” (copy of the original) |
| \(A′\) | “a prime” (copy of point \(A\)) |
| \(A′′\) | “a double prime” (second copy) |
What if you enlarged or reduced a triangle without changing its shape? How could you find the scale factor by which the triangle was stretched or shrunk?
Example \(\PageIndex{1}\)
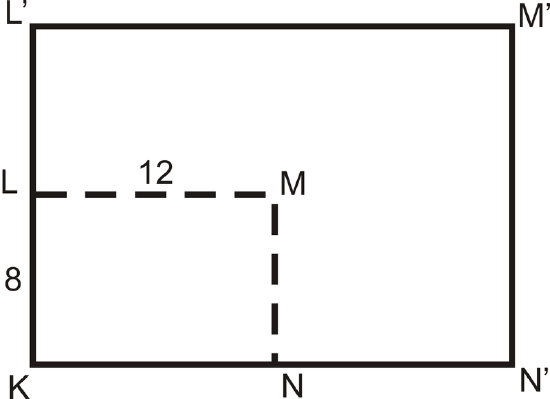
Find the perimeters of \(KLMN\) and \(K′L′M′N′\). Compare this ratio to the scale factor.
Solution
The perimeter of \(KLMN=12+8+12+8=40\). The perimeter of \(K′L′M′N′=24+16+24+16=80\). The ratio is 80:40, which reduces to 2:1, which is the same as the scale factor.
Example \(\PageIndex{2}\)
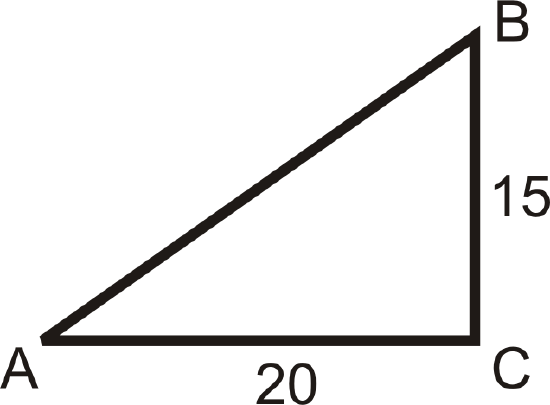
\(\Delta ABC\) is a dilation of \(\Delta DEF\). If P is the center of dilation, what is the scale factor?
Solution
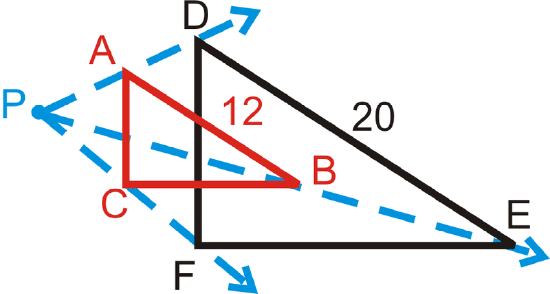
Because \(\Delta ABC\) is a dilation of \(\Delta DEF\), then \(\Delta ABC\sim \Delta DEF\). The scale factor is the ratio of the sides. Since \(\Delta ABC\) is smaller than the original, \(\Delta DEF\), the scale factor is going to be less than one, \(\dfrac{12}{20}=\dfrac{3}{5}\).
If \(\Delta DEF\) was the dilated image, the scale factor would have been \(\dfrac{5}{3}\).
Example \(\PageIndex{3}\)
The center of dilation is \(P\) and the scale factor is 3.
Find \(Q′\).
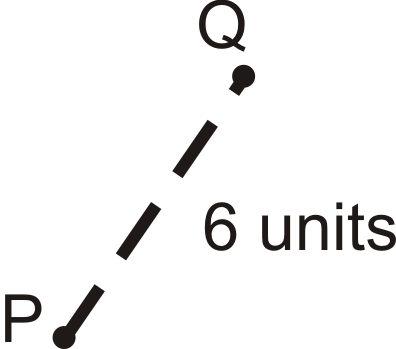
Solution
If the scale factor is 3 and \(Q\) is 6 units away from \(P\), then \(Q′\) is going to be \(6\times 3=18\) units away from \(P\). The dilated image will be on the same line as the original image and center.
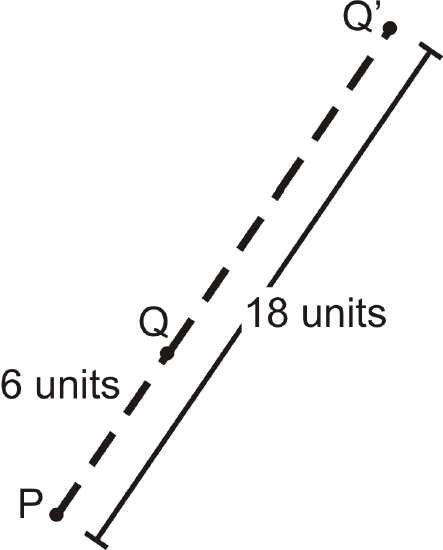
Example \(\PageIndex{4}\)
Using the picture above, change the scale factor to 13.
Find \(Q′′\) using this new scale factor.
Solution
The scale factor is \(\dfrac{1}{3}\), so \(Q′′\) is going to be \(6\times \dfrac{1}{3}=2\) units away from \(P\). \(Q′′\) will also be collinear with \(Q\) and center.
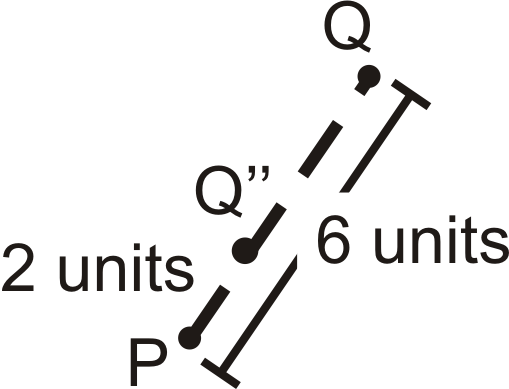
Example \(\PageIndex{5}\)
\(KLMN\) is a rectangle. If the center of dilation is \(K\) and \(k=2\), draw \(K′L′M′N′\).
Solution
If \(K\) is the center of dilation, then \(K\) and \(K′\) will be the same point. From there, \(L′\) will be 8 units above \(L\) and \(N′\) will be 12 units to the right of \(N\).
Review
For the given shapes, draw the dilation, given the scale factor and center.
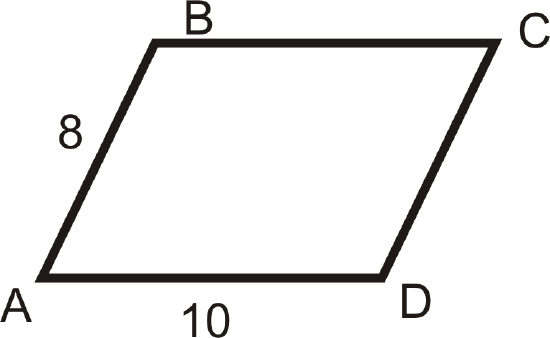
- \(k=3.5\), center is \(A\)
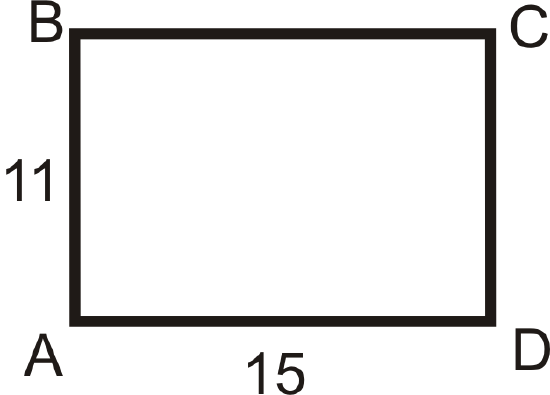
- \(k=2\), center is \(D\)
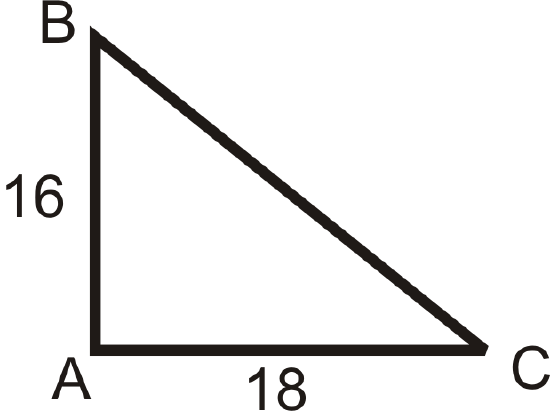
- \(k=\dfrac{3}{4}\), center is \(A\)
- \(k=\dfrac{2}{5}\), center is A\)
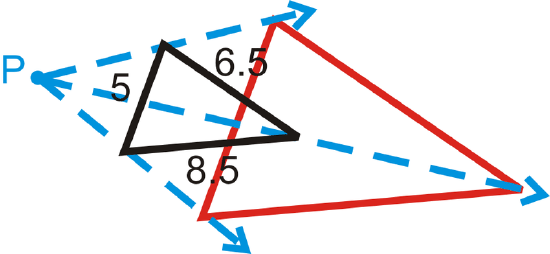
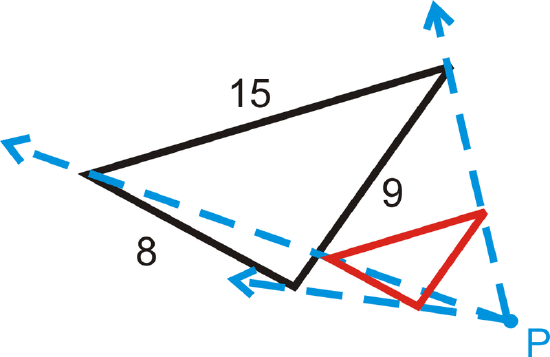
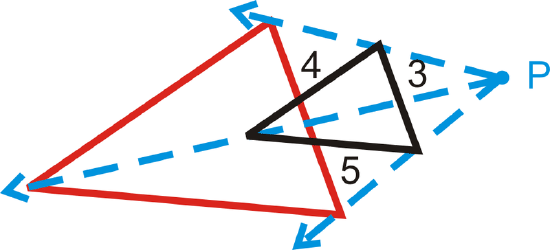
In the four questions below, you are told the scale factor. Determine the dimensions of the dilation. In each diagram, the black figure is the original and \(P\) is the center of dilation.
- \(k=4\)
- \(k=\dfrac{1}{3}\)
- \(k=2.5\)
- \(k=\dfrac{1}{4}\)
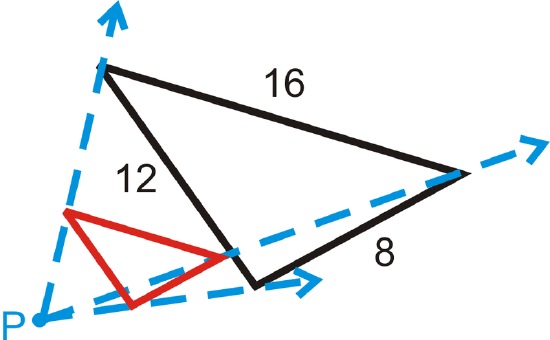
In the three questions below, find the scale factor, given the corresponding sides. In each diagram, the black figure is the original and \(P\) is the center of dilation.
-
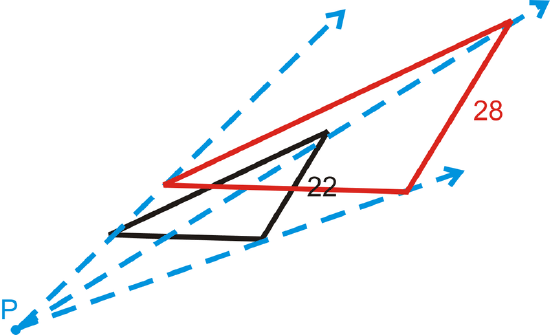
Figure \(\PageIndex{17}\) -
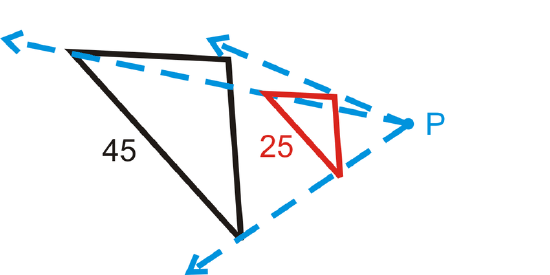
Figure \(\PageIndex{18}\) -
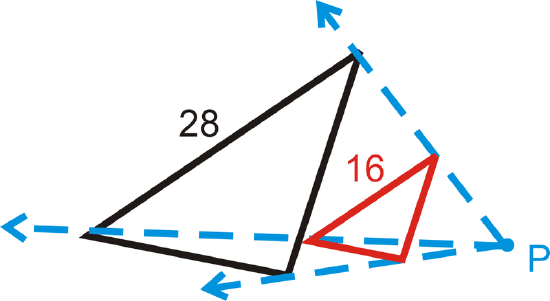
Figure \(\PageIndex{19}\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 7.11.
Vocabulary
| Term | Definition |
|---|---|
| Dilation | To reduce or enlarge a figure according to a scale factor is a dilation. |
| Quadrilateral | A quadrilateral is a closed figure with four sides and four vertices. |
| Ratio | A ratio is a comparison of two quantities that can be written in fraction form, with a colon or with the word “to”. |
| Scale Factor | A scale factor is a ratio of the scale to the original or actual dimension written in simplest form. |
| Transformation | A transformation moves a figure in some way on the coordinate plane. |
| Vertex | A vertex is a point of intersection of the lines or rays that form an angle. |
| Rigid Transformation | A rigid transformation is a transformation that preserves distance and angles, it does not change the size or shape of the figure. |
Additional Resources
Interactive Element
Video: Dilation Principles - Basic
Activities: Dilation Discussion Questions
Study Aids: Types of Transformations Study Guide
Practice: Dilation of a Shape
Real World: The CSI Effect