7.16: Dilation in the Coordinate Plane

Multiplication of coordinates by a scale factor given the origin as the center.

Dilation in the Coordinate Plane

Two figures are similar if they are the same shape but not necessarily the same size. One way to create similar figures is by dilating. A dilation makes a figure larger or smaller such that the new image has the same shape as the original.

Dilation: An enlargement or reduction of a figure that preserves shape but not size. All dilations are similar to the original figure.

Dilations have a center and a scale factor. The center is the point of reference for the dilation and the scale factor tells us how much the figure stretches or shrinks. A scale factor is labeled \(k\). Only positive scale factors, \(k\), will be considered in this text.

If the dilated image is smaller than the original, then \(0<k<1\).

If the dilated image is larger than the original, then \(k>1\).

To dilate something in the coordinate plane, multiply each coordinate by the scale factor. This is called mapping. For any dilation the mapping will be \((x,y)\rightarrow (kx,ky)\). In this text, the center of dilation will always be the origin.

What if you were given the coordinates of a figure and were asked to dilate that figure by a scale factor of 2? How could you find the coordinates of the dilated figure?

For Examples 1 and 2, use the following instructions:

Given A and the scale factor, determine the coordinates of the dilated point, \(A′\). You may assume the center of dilation is the origin. Remember that the mapping will be \((x, y)\rightarrow (kx, ky)\).

Example \(\PageIndex{1}\)

\(A(−4,6), k=2\)

Solution

\(A′(−8,12)\)

Example \(\PageIndex{2}\)

\(A(9,−13), k=\dfrac{1}{2}\)

Solution

\(A′(4.5,−6.5)\)

Example \(\PageIndex{3}\)

Quadrilateral EFGH\) has vertices \(E(−4,−2)\), \(F(1,4)\), \(G(6,2)\) and \(H(0,−4)\). Draw the dilation with a scale factor of 1.5.

Figure \(\PageIndex{1}\)

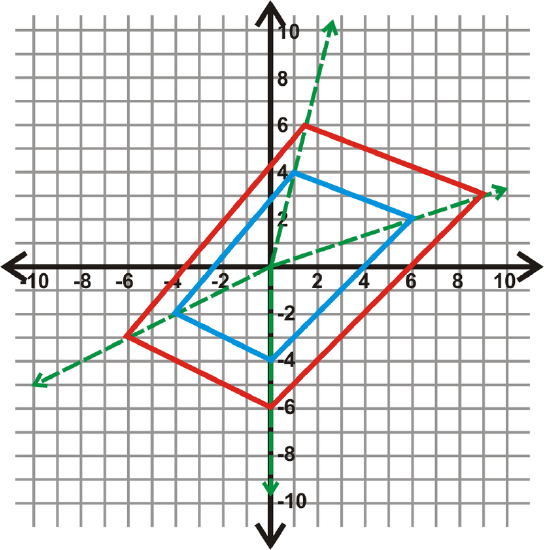
Solution

Remember that to dilate something in the coordinate plane, multiply each coordinate by the scale factor.

For this dilation, the mapping will be \((x,y)\rightarrow (1.5x, 1.5y) .

\(\begin{aligned} &E(−4,−2)\rightarrow (1.5(−4),1.5(−2))\rightarrow E′(−6,−3) \\ &F(1,4)\rightarrow (1.5(1),1.5(4))\rightarrow F′(1.5,6) \\ &G(6,2)\rightarrow (1.5(6),1.5(2))\rightarrow G′(9,3) \\ &H(0,−4)\rightarrow (1.5(0),1.5(−4))\rightarrow H′(0,−6)\end{aligned}\)

In the graph above, the blue quadrilateral is the original and the red image is the dilation.

Example \(\PageIndex{4}\)

Determine the coordinates of \(\Delta ABC\) and \(\Delta A′B′C′\) and find the scale factor.

Figure \(\PageIndex{2}\)

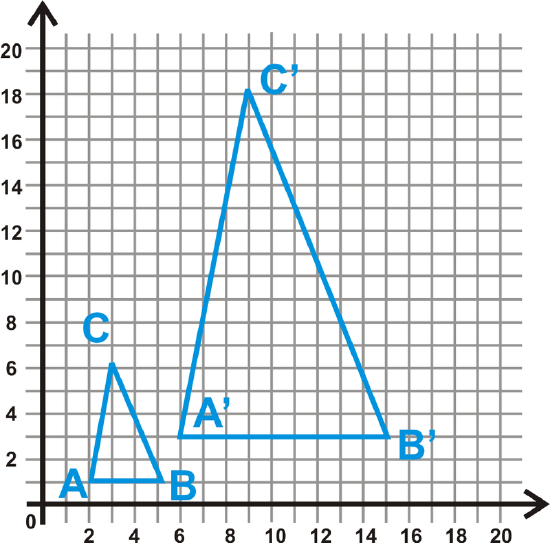
Solution

The coordinates of the vertices of \(\Delta ABC\) are \(A(2,1)\), B(5,1)\) and C(3,6)\). The coordinates of the vertices of \(\Delta A′B′C′\) are A′(6,3)\), \(B′(15,3)\) and C′(9,18)\). Each of the corresponding coordinates are three times the original, so \(k=3\).

Example \(\PageIndex{5}\)

Show that dilations preserve shape by using the distance formula. Find the lengths of the sides of both triangles in Example B.

Solution

\(\begin{array}{ll} \underline{\Delta ABC} & \underline{\Delta A'B'C'}
A B=\sqrt{(2-5)^{2}+(1-1)^{2}}=\sqrt{9}=3 & A^{\prime} B^{\prime}=\sqrt{(6-15)^{2}+(3-3)^{2}}=\sqrt{81}=9 \\
A C=\sqrt{(2-3)^{2}+(1-6)^{2}}=\sqrt{26} & A^{\prime} C^{\prime}=\sqrt{(6-9)^{2}+(3-18)^{2}}=3 \sqrt{26} \\
C B=\sqrt{(3-5)^{2}+(6-1)^{2}}=\sqrt{29} & C^{\prime} B^{\prime}=\sqrt{(9-15)^{2}+(18-3)^{2}}=3 \sqrt{29}
\end{array} \)

From this, we also see that all the sides of \(\Delta A′B′C′\) are three times larger than \(\Delta ABC\).

Review

Given \(A\) and \(A′\), find the scale factor. You may assume the center of dilation is the origin.

1. \(A(8,2), A′(12,3)\)
2. \(A(−5,−9), A′(−45,−81)\)
3. \(A(22,−7), A(11,−3.5)\)

The origin is the center of dilation. Draw the dilation of each figure, given the scale factor.

4. \(A(2,4), B(−3,7), C(−1,−2); k=3\)
5. \(A(12,8), B(−4,−16), C(0,10); k=34\)

Multi-Step Problem Questions 6-9 build upon each other.

6. Plot \(A(1,2), B(12,4), C(10,10)\). Connect to form a triangle.
7. Make the origin the center of dilation. Draw 4 rays from the origin to each point from #21. Then, plot \(A′(2,4), B′(24,8), C′(20,20)\). What is the scale factor?
8. Use \(k=4\), to find \(A′′B′′C′′\). Plot these points.
9. What is the scale factor from \(A′B′C′\) to \(A′′B′′C′′\)?

If \(O\) is the origin, find the following lengths (using 6-9 above). Round all answers to the nearest hundredth.

10. \(OA\)
11. \(AA′\)
12. \(AA′′\)
13. \(OA′\)
14. \(OA′′\)
15. \(AB\)
16. \(A′B′\)
17. \(A′′B′′\)
18. Compare the ratios \(OA:OA′\) and \(AB: A′B′\). What do you notice? Why do you think that is?
19. Compare the ratios \(OA:OA′′\) and \(AB: A′′B′′\). What do you notice? Why do you think that is?

Review (Answers)

To see the Review answers, open this PDF file and look for section 7.12.

Vocabulary

Term	Definition
Dilation	To reduce or enlarge a figure according to a scale factor is a dilation.
Distance Formula	The distance between two points \((x_1,y_1)\) and \((x_2,y_2)\) can be defined as \(d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}\).
Mapping	Mapping is a procedure involving the plotting of points on a coordinate grid to see the behavior of a function.
Scale Factor	A scale factor is a ratio of the scale to the original or actual dimension written in simplest form.

Additional Resources

Interactive Element

Video: Dilation in the Coordinate Plane Principles - Basic

Activities: Dilation in the Coordinate Plane Discussion Questions

Study Aids: Types of Transformations Study Guide

Practice: Dilation in the Coordinate Plane